加重移動平均法
解析手法の役割
加重移動平均は時系列データの傾向を調べる解析手法で、季節不規則変動調整済み系列TCを算出します。
TCIをTCで割ることによってIを算出します。
適用できるデータ形態と時期数
月次データ、四半期データ、年次データ、日別データなど全ての時間変数に適用できます。
データの時期数はどのデータ形態も4以上です。
<具体例> 下記表は売上本数のデータです。

加重移動平均の求め方
当該月の前後1ヵ月の3ヵ月間の平均を「移動平均」といいます。
加重移動平均の求め方は、移動平均同様に当該月の前後1ヵ月のデータを用いますが、平均を求める際、当該月を2倍した合計値を4で割って算出します。(2倍したデータを用いたので3ではなく4で割ります。)
2月の場合 (1月 + 2×2月 + 3月) ÷ 4ヵ月 =(2+2×3+4)÷4=3
3月の場合 (2月 + 2×3月 + 4月) ÷ 4ヵ月 =(3+2×4+8)÷4=4.75
前の月がない1月と後の月がない8月は、移動平均は計算できませんでしたが、加重移動平均は次のようにして求めることができます。1月は前の月のデータがないので加重移動平均は次となります。
1月の場合 ( 2×1月 + 2月) ÷ 3ヵ月 =( 2×2+3 )÷3=2.333
8月は後の月のデータがないので加重移動平均は次となります。
8月の場合 (7月 + 2×8月 ) ÷ 3ヵ月 =( 5+2×12 )÷3=9.667
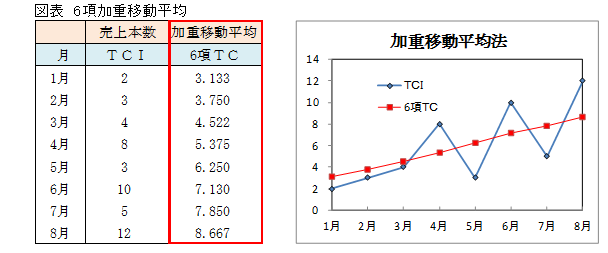
1月から8月の加重移動平均を示します。
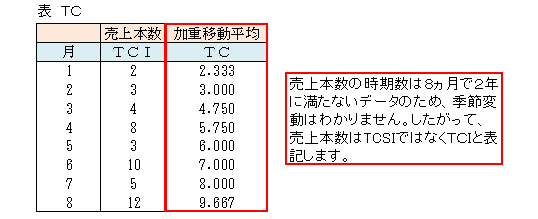
加重移動平均からわかること
売上本数(TCI)と加重移動平均のグラフを重ね書きします。
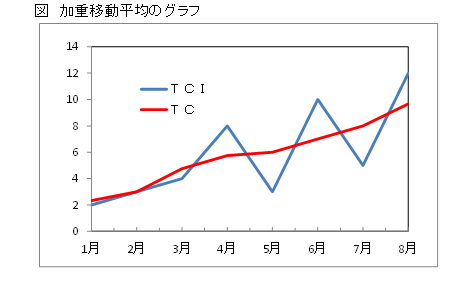
TCの線はTCIの折れ線の真ん中を通り、TCの変動はTCIに比べ小さくなっています。
したがって、TCはTCIに比べ売上本数の傾向が捉えやすくなっています。
移動平均に比べ、TCの線が滑らかになることが知られています。
移動平均は計算できない月がありましたが、加重移動平均は全ての月について計算できます。
TCの把握は移動平均より加重移動平均で行うのがよいでしょう。
<留意点>
移動の期間(3ヵ月間、3四半期間、3年間、・・・)を項数あるいはサイクルといいます。
項数は3だけでなく、それ以上の加重移動平均を求めることができます。
項数が奇数、偶数どちらでも加重移動平均を算出できます。
項数が奇数と偶数で求め方が異なります。
項数が奇数の場合
加重移動平均は、次に示すウエイトをデータに掛けて加重移動合計を算出し、加重移動合計をウエイト合計で割ることによって求められます。
ウエイトは加重移動平均を求める時期を最大とし、その時期から離れるに従い小さくなる値とします。
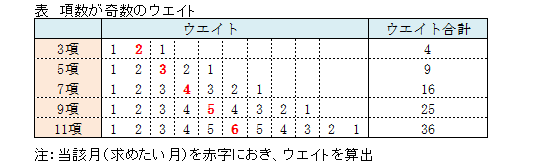
先ほどは3項の加重移動平均でした。
ここでは下記データについて、5項の加重移動平均の算出方法を説明します。

<4月における5項加重移動平均>
加重移動合計=1×2月+ 2×3月 + 3×4月 + 2×5月 + 1×6月
=1×3 + 2×4 + 3×8 + 2×3 + 1×10 =51
ウエイト合計=1+2+3+2+1=9
加重移動平均 = 加重移動合計 ÷ ウエイト合計 = 51÷ 9=5.667
時系列データの先頭あるいは末尾部分は、計算対象のデータが存在しないので、下記に示すような短縮加重を行うことによって、加重移動平均を算出します。
この例では、1月、2月、7月、8月が計算対象のデータが存在しません。
2月の短縮加重移動を示します。
<2月における5項加重移動平均>
加重移動合計=2×1月+ 3×2月 + 2×3月 + 1×4月 ← 12月のデータ無し・短縮加重移動を行います
=2×2 + 3×3 + 2×4 + 1×8 = 29
ウエイト合計=2+3+2+1=8
加重移動平均= 加重移動合計 ÷ ウエイト合計 = 29÷8=3.625
全ての月について、5項加重移動平均を求めました。
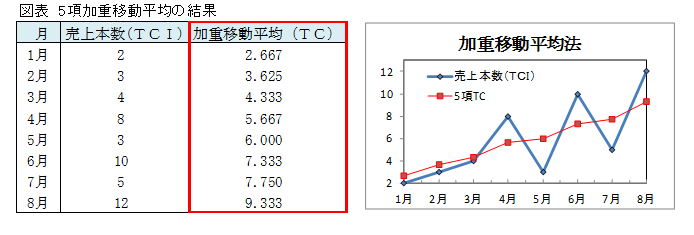
項数が偶数の場合
3月の4項加重移動平均の求め方を説明します。

3月の3項加重移動平均は「2月,3月,4月」において3月が真ん中に位置しますが、3月の4項加重移動平均は「1月,2月,3月,4月」、「2月,3月,4月,5月」どちらの4ヵ月を使うにしても、3月は真ん中に位置しません。そこで下記に示すウエイトをデータに掛け、2つの加重移動合計を加算し2で割った値を3月の4項加重移動合計とし、ウエイト合計で割ることによって3月の4項加重移動平均を求めます。
<3月の4項加重移動平均>
◆ 加重移動合計
1つ目の加重移動合計 1×1月 + 2×2月 + 2×3月 + 1×4月
2つ目の加重移動合計 1×2月 + 2×3月 + 2×4月 + 1×5月
上記2つの加算は次で示せます。
1×1月 + 3×2月 + 4×3月 + 3×4月 + 1×5月
3月の4項加重移動合計は上記ウエイトを2で割り求められます。
3月の4項加重移動合計 =
0.5×1月 + 1.5×2月 + 2×3月 + 1.5×4月 + 0.5×5月 =
0.5×2 + 1.5×3 + 2×4 + 1.5×8 + 0.5×3 = 27
◆ウエイト合計
上記のウエイトを加算します。
0.5+1.5+2+1.5+0.5=6
◆加重移動平均
加重移動平均は加重移動合計 ÷ ウエイト合計で求められます。
3月の4項加重移動平均=27÷6=4.5
上記に従い、4月の6項の加重移動平均を算出します。
◆ 加重移動合計
1つ目の加重移動合計 =1×1月 + 2×2月 + 3×3月 + 3×4月 + 2×5月 + 1×6月
2つ目の加重移動合計 =1×2月 + 2×3月 + 3×4月 + 3×5月 + 2×6月 + 1×7月
上記2つを加算し、ウエイトを2つで割ります。
4月の6項加重移動合計 =
(1×1月 + 3×2月 + 5×3月 + 6×4月 + 5×5月 + 3×6月 + 1×7月)÷2 =
0.5×1月 + 1.5×2月 + 2.5×3月 + 3×4月 + 2.5×5月 + 1.5×6月 + 0.5×7月 =
0.5×2 + 1.5×3 + 2.5×4 + 3×8 + 2.5×3 +1.5×10 + 0.5×5 =64.5
◆ウエイト合計
0.5+1.5+2.5+3+2.5+1.5+0.5=12
◆加重移動平均
4月の6項加重移動平均=加重移動合計 ÷ ウエイト合計=64.5 ÷ 12=5.375
8項目以降も同様の考え方でウエイトを求められます。項数が4項、6項、8項、10項、12項についてのウエイトを示します。
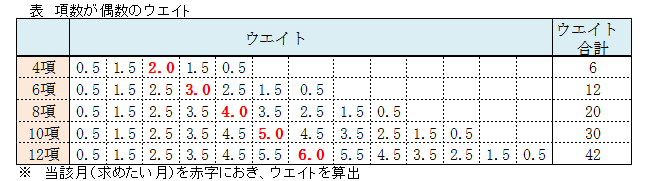
<項数が偶数の場合の短縮加重>
時系列データの先頭あるいは末尾部分で、計算対象のデータが存在しない場合は、先に示した短縮加重を行うことによって、加重移動平均を算出します。
◆1月の6項加重移動合計 (項数が偶数のウエイト表より)
=3×1月 + 2.5×2月 + 1.5×3月 + 0.5×4月 ←10月,11月,12月のデータ無し・短縮加重移動を行います
=3×2 + 2.5×3 + 1.5×4 +0.5×8 =23.5
◆ウエイト合計 3+2.5+1.5+0.5=7.5
◆1月の加重移動平均=23.5÷7.5=3.133
全ての月について、6項加重移動平均を求めました。
<6項目加重移動平均の結果>
加重移動平均の項数
加重移動平均の項数が多いほど、傾向変動は滑らかになります。
「月別平均法」で、販売戸数(TCSI)から季節変動を除去したTCIを算出しました。
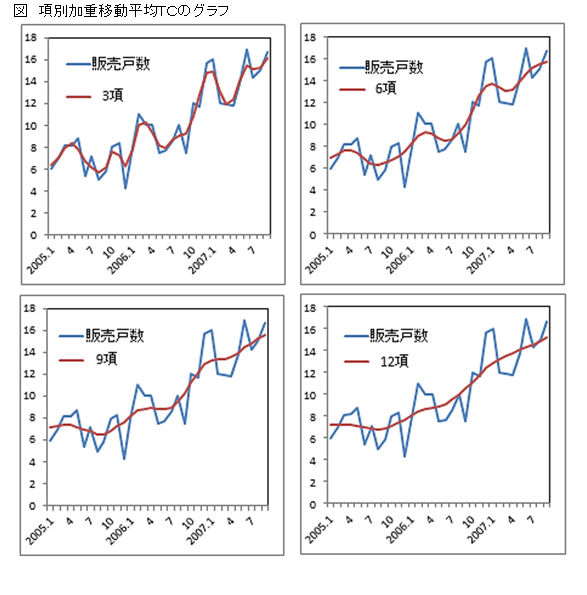
このTCIのデータに、3項、6項、9項、12項の加重移動平均を算出しました。
下に示すグラフで、4つのTCを比較しました。項数が多いTCほど、滑らかな線になっています。
<留意点>
項数を多くするほど時系列データの傾向が見えてきますが、一方で先頭部分や末尾部分は短縮加重で計算されているため、今後、データが出そろった時点で計算された傾向変動と必ずしも一致しません。したがって項数がいくつあれば良いという基準はありません。
解説者は、月次データの場合、月数が23ヵ月以下であれば3項、24ヵ月以上であれば12項としています。求められた傾向変動に3傾向線を当てはめれば傾向を把握できるので、加重移動平均の項数は3項か12項でよいと判断しています。
販売戸数の時期数は24ヵ月以上なので、上のグラフからわかるように12項の加重移動平均が最も滑らかになり12項が良いといえます。
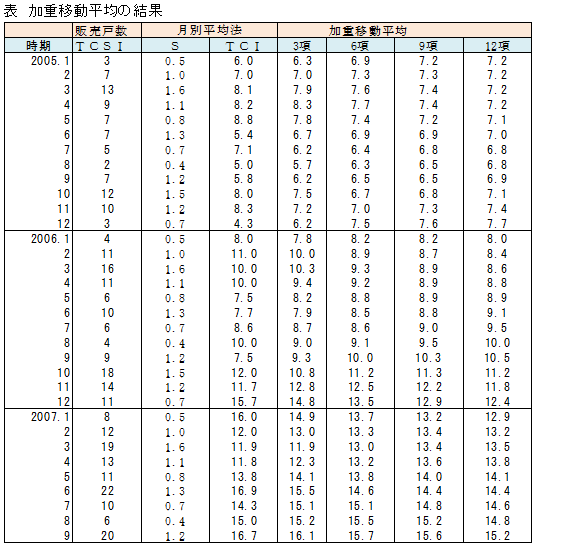
不規則変動指数Iの算出
TCIを加重移動平均で求めたTCで割ることによって、不規則変動指数Iを算出できます。求められたIから、傾向変動の周りを不規則に変動する動きを把握することができます。
Iは指数で求められ、1より大きい(小さい)とき、法規税制の改定、キャンペーン有無など不規則変動要因が売上の増加(減少)に影響を及ぼしたといえます。
上記データでIを算出しました。
加重移動平均は12項TCを用いました。
【計算例】
2005年1月のI = 2005年1月のTCI ÷ 2005年1月の12項TC = 6.0 ÷ 7.2 = 0.83
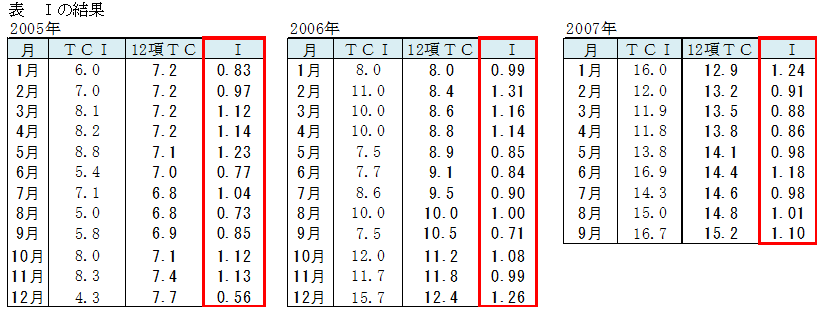
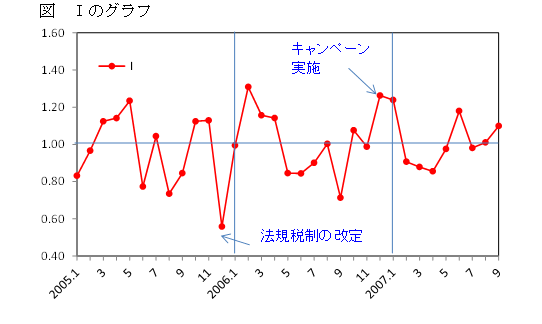
2005年12月のIは0.56と1を大きく下回っています。
この月に法規税制の改定があり、売上は大きなダメージを受け減少したことがわかります。
2006年12月のIは1.26で1を上回っています。
この月はキャンペーンを実施し、その効果があり売上が増えたことがわかります。



