EPA法 ≪ 2 /2 ≫
EPA法の計算方法
EPA法の計算方法は複雑で、以下の計算方法は興味ある方のみ読んでください。
手順No.(0)のTCSIは医療機器販売台数のデータです。
このデータに、手順No.1~28の計算をすることにより、TCI、TC、S、Iを算出できます。
(1)TC_1 TCの近似値算出
右表の(0)のTCSIに「12項移動平均」を適用し、TCの近似値TC_1を算出。
(2)SI _1 SIの近似値算出
(0)のTCSI ÷ (1)のTC_1 より、SIの近似値SI_1を算出。
(3) SO_1 SIの調整
(2)のSI_1に3項の「各年同月対象加重移動平均」を適用しSO_1を算出。
【計算例】 2011年7月 =(2×2011年7月+2012年7月)÷3
=(2×0.832+0.939)÷3=0.867
注.上式を計算すると0.868となりますが、計算対象の数値は下記に示すように表記を丸められています。 0.832→0.83184 0.939→0.938547
よって、以下手計算で求めた結果と表記されている結果が合わない部分がありますが、不一致の指摘は致しませんこと、ご了解ください。
【計算例】 2013年1月=(2012年1月+2×2013年1月)÷3
=(1.057+2×0.745)÷3=0.849
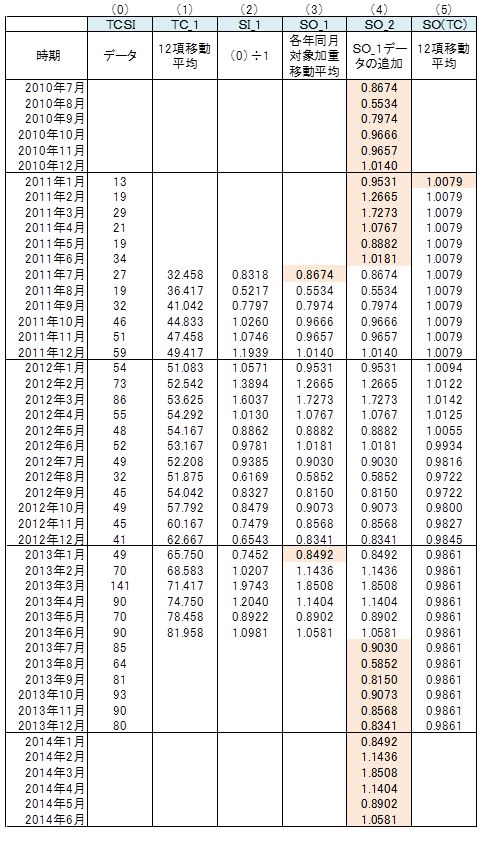
(4)SO_2 (3)のSO_1 のデータ追加
(3)のSO_1の前後12ヵ月間のデータを追加し、SO_2を作成。
SO_1の2011年7月~2012年6月= SO_2の2010年7月~2011年6月
SO_1の2012年7月~2013年6月= SO_2の2013年7月~2014年6月
(5)SO(TC) SIの調整
(4)のSO_2に「12項移動平均を」適用し、SO(TC)を算出。
【計算例】2011年1月の12項移動平均
(0.5×2010年7月+2010年8月+2010年9月+2010年10月+2010年11月+2010年12月+2011年1月+2011年2月+2011年3月+2011年4月+2011年5月+2011年6月+0.5×2011年7月)÷12 =(0.5×0.867+0.553+0.797+ ・・・+1.018+0.5×0.867)÷12=1.0079
(6)S_1 Sの近似値算出
(4)のSO_2 ÷ (5)のSO(TC)_1 より、Sの近似値S_1を算出。
(7)S_2 Sの近似値を算出
(6)のS_1に3項の「各年同月対象加重移動平均」を適用しSの近似値S_2を算出。
【計算例】2011年7月
(2×2011年7月+2012年7月)÷3 =(2×0.8606+0.9199)÷3 =0.8804
【計算例】2013年1月
(2012年1月+2×2013年1月)÷3=(0.9443+2×0.8611)÷3 =0.8889
(8)TCI_1 TCIの近似値算出
(0)のTCSI ÷ (7)のS_2 より、TCIの近似値TCI_1を算出。
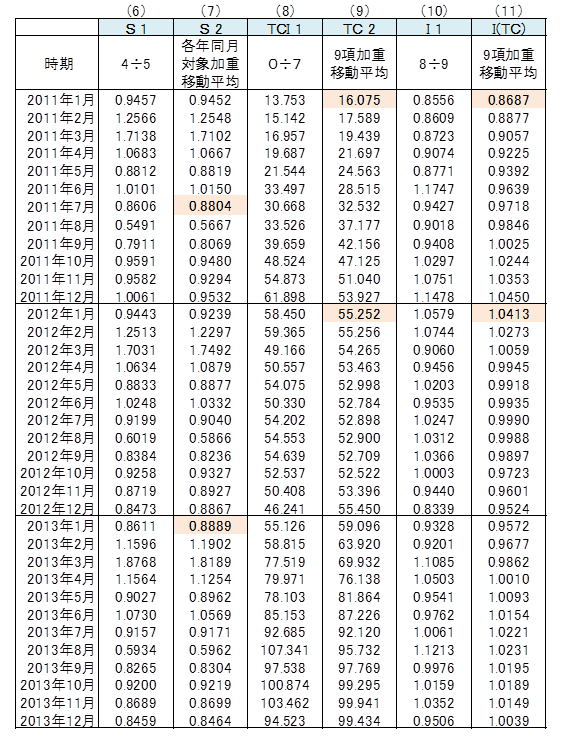
(9)TC_2 TCの近似値算出
(8)のTCI_1に「9項加重移動平均」を適用し、TC_2を算出。
【計算例】2011年1月の9項加重移動平均
(5×2011年1月+4×2011年2月+3×2011年3月+2×2011年4月+2011年5月)÷15=(5×13.753+4×15.142+3×16.957+2×19.687+21.544)÷15=16.075
【計算例】2012年1月の9項加重移動平均
(2011年9月+2×2011年10月+3×2011年11月+4×2011年12月+5×2012年1月+4×2012年2月+3×2012年3月+2×2012年4月+2012年5月)÷25=(39.659+2×48.524+3×54.873+4×61.898+5×58.450+4×59.365+3×49.166+2×50.557+54.075)÷25=55.252
(10)I_1 Iの近似値算出
(8)のTCI_1 ÷ (9)のTC_2 より、Iの近似値I_1を算出。
(11)I(TC) Iの調整
(10)のI_1に「9項加重移動平均」を適用し、I(TC)を算出。
【計算例】2011年1月の9項加重移動平均
=(5×2011年1月+4×2011年2月+3×2011年3月+2×2011年4月+2011年5月)÷15 =(5×0.8556+4×0.8609+3×0.8723+2×0.9074+0.8771)÷15=0.8687
【計算例】2012年1月の9項加重移動平均
(2011年9月+2×2011年10月+3×2011年11月+4×2011年12月+5×2012年1月+4×2012年2月+3×2012年3月+2×2012年4月+2012年5月)÷25 =(0.9408+2×1.0297+3×1.0751+4×1.1478+5×1.0579+4×1.0744+3×0.9060+2×0.9456+1.0203)÷25 =1.041
(12)TC_3 TCの近似値算出
(9)のTC_2 × (11)のI(TC) より、TCの近似値TC_3を算出。
(13)SI_2 SIの近似値を算出
(0)のTCSI ÷ (12)のTC_3 より、SIの近似値SI_2を算出。
(14)SO_2 SIの調整
(13)のSI_2に7項の「各年同月対象加重移動平均」を適用しSO_2を算出。
【計算例】2011年7月
(4×2011年7月+3×2012年7月+2×2013年7月)÷9
=(4×0.8541+3×0.9272+2×0.9028)÷9 =0.8893
【計算例】2012年1月
(3×2011年1月+4×2012年1月+3×2013年1月)÷10
=(3×0.9310+4×0.9385+3×0.8662)÷10=0.9146
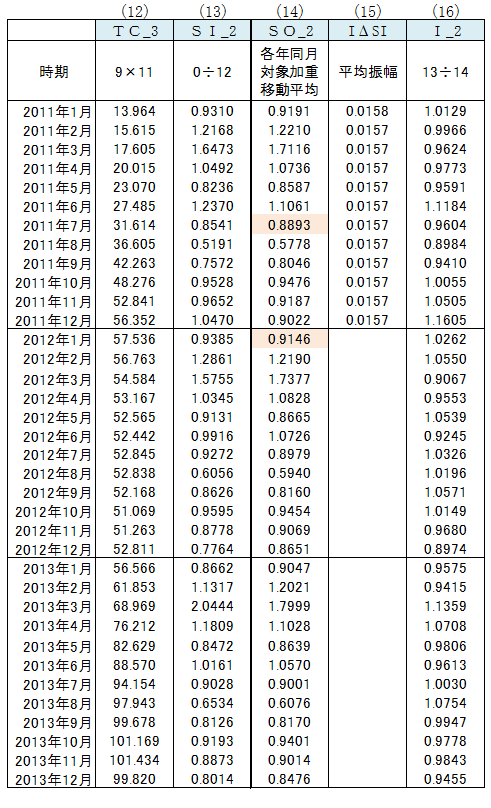
(15)IΔSI 平均振幅を算出
(14)のSO_2の各月の経年変化率から平均振幅を算出。
【計算例】1月 ※マイナスはプラスとする
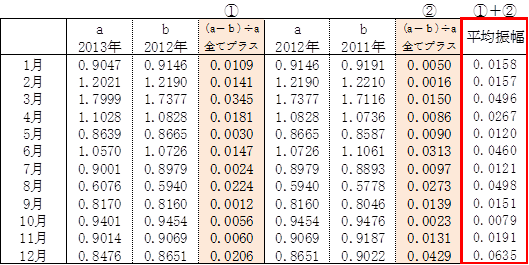
① (0.9047-0.9146)÷0.9047=0.0109
② (0.9146-0.9191)÷0.9146=0.0050
平均振幅=①+②=0.0109+0.0050=0.0158
(16)I_2 Iの近似値を算出
(13)のSI_2 ÷ (14)のSO_2 より、Iの近似値I_2を算出。
(17)IΔII 平均振幅を算出
(16)のI_2の各月の経年変化率から平均振幅を算出。
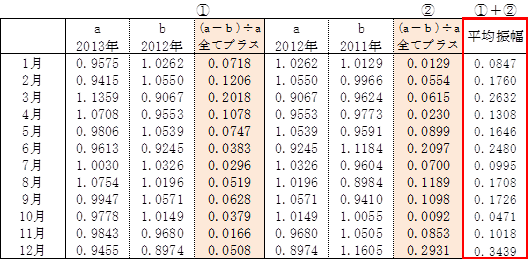
【計算例】1月 ※マイナスはプラスとする
①(0.9575-1.0262)÷0.9575=0.0718
②(1.0262-1.0129)÷1.0262=0.0129
平均振幅=①+②=0.0718+0.00129=0.0847
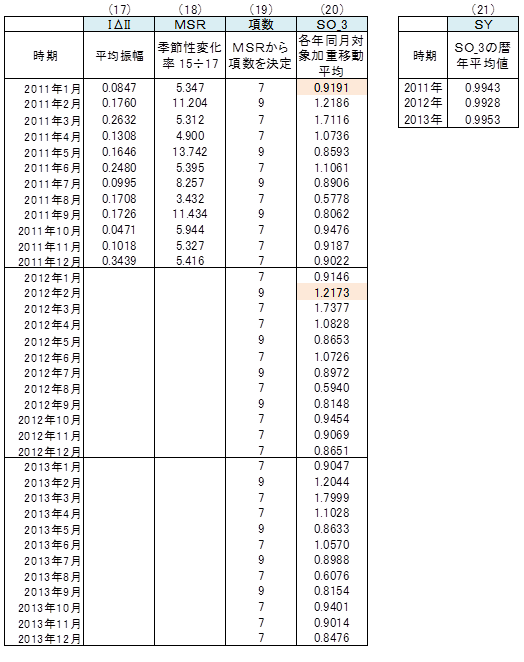
(18)MSR 季節性変化率を算出
(17)のIΔII ÷ (15)のIΔSI より、季節性変化率MSRを算出
(19)項数の決定 各年同月対象加重移動平均の項数を決定
(20)のSO_3の算出は「各年同月対象加重移動平均」を適用するが、その際の項数は MSRの大きさによって決める。
MSR<1.5・・・3項 1.5≦MSR<3・・・5項 3≦MSR<6・・・ 7項 MSR≧6・・・ 9項
(20)SO_3 Sの調整
(13)のSI_2に3項~9項のいずれかの「各年同月対象加重移動平均」を適用し、SO_3を算出。ただし、項数はMSRの大きさによって決める。
注.MSR(季節性変化率)が大きいSI_2は、項数の大きい
「各年同月対象加重移動平均」を適用することにより、変動がより小さいSO_3が求められる。
【計算例】2011年1月 7項
(4×2011年1月+3×2012年1月+2×2013年1月)÷9 =(4×0.9310+3×0.9385+2×0.8662)÷9 =0.9191
【計算例】2012年2月 9項
(4×2011年2月+5×2012年2月+4×2013年2月)÷13 =(4×1.2168+5×1.2861+4×1.1317)÷13 =1.2173
(21)SY SO_3 の暦年平均値
各年のSO_3 の平均値SYを算出。
(22)S 最終Sの算出
(20)のSO_3 ÷ (21)のSY より、最終のSを算出。
【計算例】2011年1月
2011年1月SO_3÷2011年SY=0.9191÷0.9943=0.9244
【計算例】2012年2月
2012年2月SO_3÷2012年SY=1.2173÷0.9928=1.2261
(22)S 来年度のSの予測
来年度のSは公式によって予測する。(3×最終年S-前年S) ÷ 2
【計算例】2014年1月
(3×2013年1月-2012年1月)÷2=(3×0.9090-0.9212)÷2=0.9029
(23)TCI 最終TCIの算出
(0)のTCSI ÷ (22)のS より、最終のTCIを算出。
(24)TC_4 TCの近似値算出
(23)のTCIに「9項加重移動平均」を適用し、TC_4を算出。
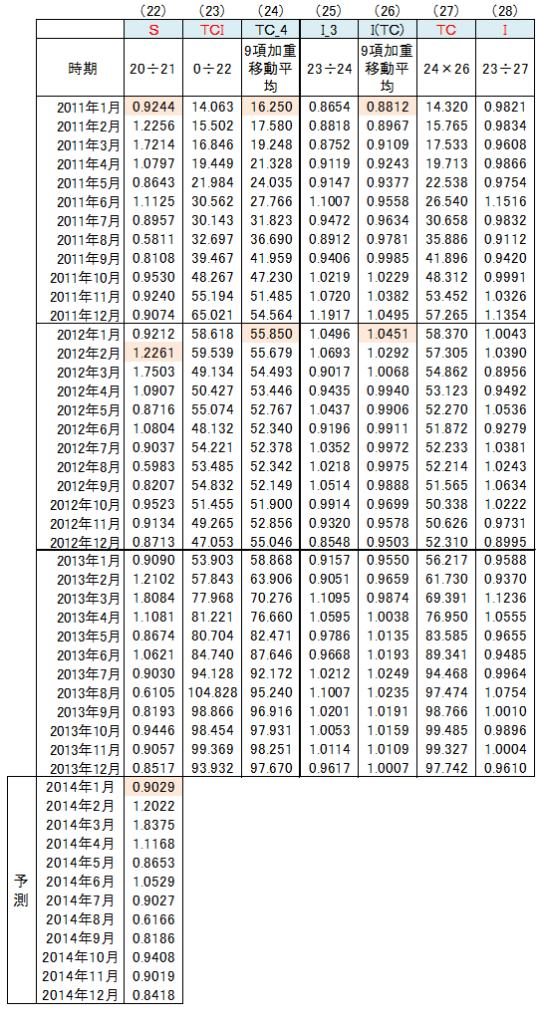
【計算例】2011年1月の9項加重移動平均
(5×2011年1月+4×2011年2月+3×2011年3月+2×2011年4月+2011年5月)÷15
=(5×14.063+4×15.502+3×16.846+2×19.449+21.984)÷15=16.250
【計算例】2012年1月の9項加重移動平均
(2011年9月+2×2011年10月+3×2011年11月+4×2011年12月+5×2012年1月+4×2012年2月+3×2012年3月+2×2012年4月+2012年5月)÷ 25=(39.467+2×48.267+3×55.194+4×65.021×58.618+4×59.539+3×49.134+2×50.427+55.074 )÷25=55.850
(25)I_3 Iの近似値算出
(23)のTCI ÷(24)のTC_4 より、Iの近似値I_3を算出。
(26)I(TC) Iの調整
(25)のI_3に「9項加重移動平均」を適用し、I(TC)を算出。
【計算例】2011年1月の9項加重移動平均
(5×2011年1月+4×2011年2月+3×2011年3月+2×2011年4月+2011年5月)÷15
=(5×0.8654+4×0.8818+3×0.8752+2×0.9119+0.9147)÷15=0.8812
【計算例】2012年1月の9項加重移動平均
(2011年9月+2×2011年10月+3×2011年11月+4×2011年12月+5×2012年1月+4×2012年2月+3×2012年3月+2×2012年4月+2012年5月)÷25=(0.9406+2×1.0219+3×1.0720+4×1.1917+5×1.0496+4×1.0693+3×0.9017+2×0.9435+1.0437)÷25
=1.0451
(27)TC 最終TCの算出
(24)のTC_4 × (26)のI(TC) より、最終のTCを算出。
(28)I 最終Iの算出
(23)のTCI ÷ (27)のTC より、最終のIを算出。
※ アイスタット開発の「EPA法ソフトウェア」は無料でダウンロードできます。
EPA法を処理するためのソフトウェアです。上記の計算過程をソフトを使いながら確認できます。
フリーソフト申し込み画面はこちら



