数量化1類の基本 ≪2/3≫
数量化1類の関係式
数量化1類の関係式は次式で表します。

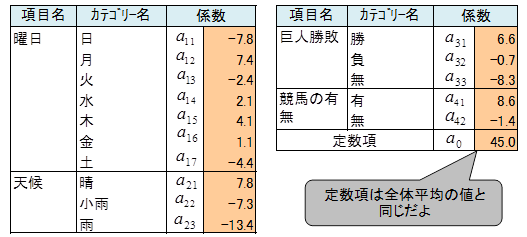
サンプルスコア
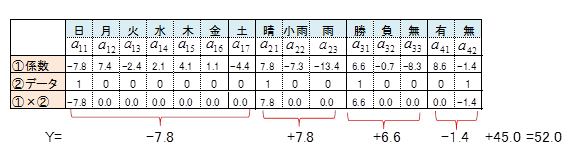
最初の日のデータを関係式に代入してYを求めます。求められたYをサンプルスコアといいます。全ての日についてサンプルスコアを求めます。
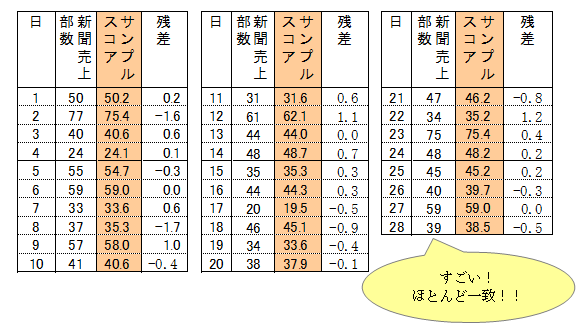
どの日も、新聞売上部数の実績値とサンプルスコアはほぼ近い値になっています。いいかえればカテゴリースコアは、実績値と理論値ができるだけ近くなるように、導かれた数値といえます。
予測
どの日についてみても、新聞売上部数の実績値とサンプルスコアの値がほぼ一致しています。これだけ一致するのだから、この関係式は予測に使えると判断します。
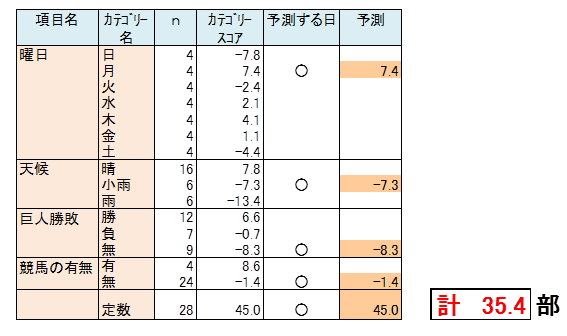
月曜日で天候は小雨、前日の巨人の試合は中止、当日および前後の日の競馬がない、という日における新聞売上部数の予測値は、関係式を用いても算出できますが、該当する日のカテゴリースコアと全体平均値の合計からも算出できます。
分析精度/決定係数
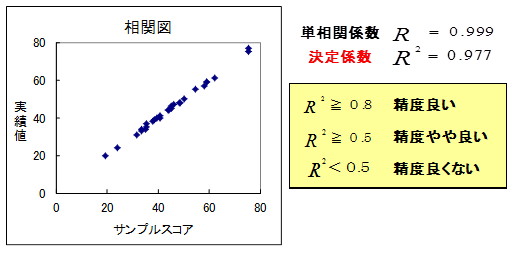
決定係数は実績値とサンプルスコアの一致度を示した指標です。
決定係数は0.977で基準の0.5を大きく上回り、すばらしい分析精度といえます。
説明変数の目的変数に対する貢献度
例題の説明変数の項目数とカテゴリー数を再確認します。項目数は4つ、カテゴリー数は15です。
15個のカテゴリーの目的変数に対する貢献度は、カテゴリースコアで把握できました。4個の項目の目的変数に対する重要度ランキングはこれから学ぶレンジ、寄与率で把握できます。それではレンジ、寄与率はどのような計算方法で求められるかを調べてみましょう。
この例題の天候のカテゴリー別平均とカテゴリースコアをA表に示しします。平均値は、晴が52部、小雨が39部、雨が32部で、カテゴリー間に差がみられます。カテゴリースコアは、晴れが8部、小雨が-7部、雨が-13部で、カテゴリー間に差がみられます。
カテゴリー別平均とカテゴリースコアの値は対応し、天候は、カテゴリー別平均に差があったからカテゴリースコアにも差があるのです。
仮に、B表のようにカテゴリー別平均に差がなければ、カテゴリースコアに差が生じないはずです。
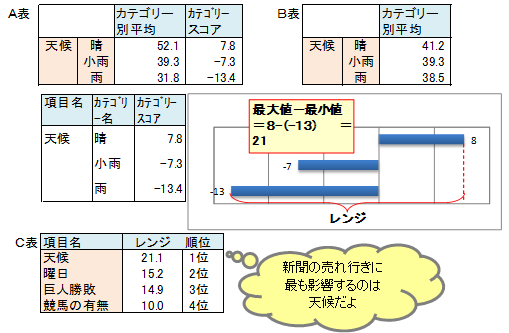
天候のようにカテゴリー別平均値にがあれば、すなわちカテゴリースコアに差があれば、天候は新聞の売れゆきに影響度の高い、重要な項目であると判断します。
カテゴリースコアに差があるかは、カテゴリースコアの最大値と最小値の格差で判断します。この値をレンジと言います。天候のレンジは、8-(-13)=21です。
各項目のレンジのレンジ合計に占める割合を寄与率といいます。レンジ、寄与率が大きい項目ほど、目的変数への影響度が大きい、重要な項目だといえます。
全ての項目についてレンジ、寄与率を求め、C表に示しました。新聞の売れ行きには天候が最も影響し、次に曜日、巨人勝敗、競馬有無が続きます。
