解析事例・多変量解析

傾向スコアマッチング分析

１．データ

健康診断の検査値の一つにγ-ＧＴＰ（ガンマジーティーピー）がある。

γ-ＧＴＰは肝臓や胆管の細胞がどれくらい壊れたかを示す指標で、検査値が成人男性の場合100(基準は50)を超えると、肝硬変、肝がん、脂肪肝、胆道疾患の可能性があるといわれている。

下記は100人の成人男性について、γ-ＧＴＰ、飲酒量(一カ月に飲酒する日数)、喫煙有無、ギャンブル嗜好(7件法)を調べたものである。

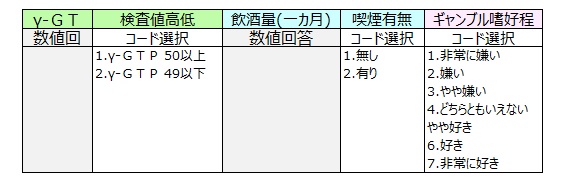
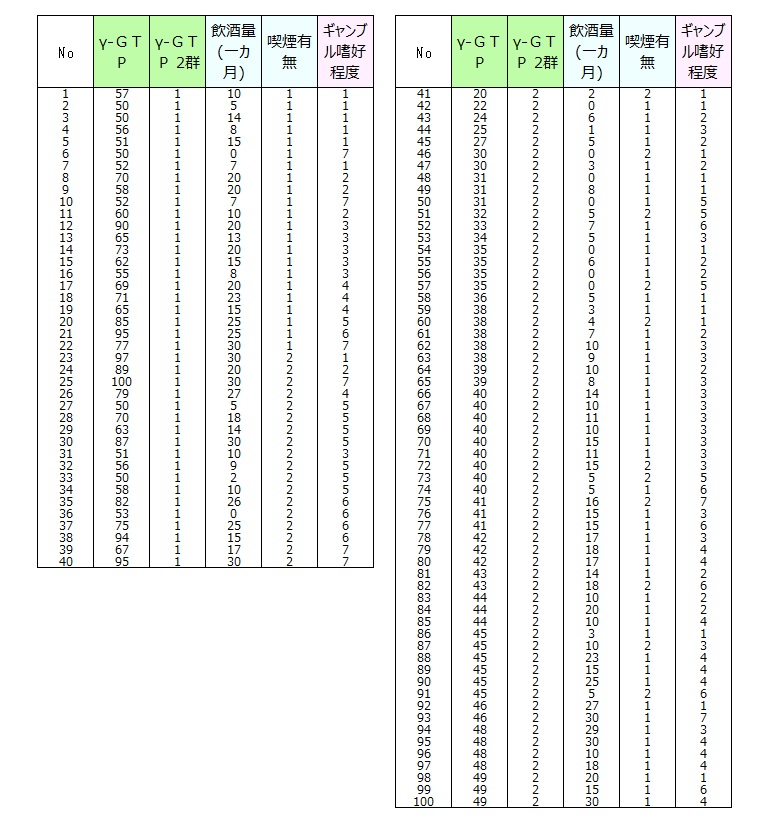
データ

２．検証内容

• 飲酒量はγ-GTPに関係があるかを検証する。
• 喫煙有無はγ-GTPに関係があるかを検証する。
• ギャンブル嗜好はγ-GTPに無関係であることを検証する。

３．γ-GTP　2群間の有意差検定

γ-GTPの「50以上」を群1=高群、「49以下」を群2=低群として、γ-GTP(2群)のデータを作成した。

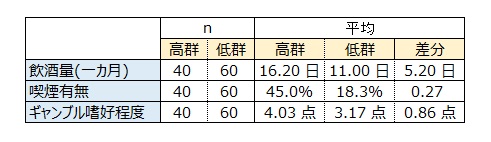
• 飲酒量の平均は、高群16.2(日)、低群11.0(日)で高群が低群を5.2ポイント上回った。ｐ値0.0037＜0.05より高群は低群に比べ有意に高いといえる。このことから、飲酒量はγ-GTPに関係があることが検証できた。
  
• 喫煙有無において「有り」の割合は、高群45.0％、低群18.3％で高群が低群を26.7ポイント上回った。ｐ値0.0037＜0.05より高群は低群に比べ有意に高いといえる。このことから、喫煙有無はγ-GTPに関係があることが検証できた。
  
• ギャンブル嗜好程度の平均は、高群4.03(点)、低群3.17(点)で高群が低群を0.86ポイント上回った。ｐ値0.0252＜0.05より高群は低群に比べ有意に高いといえる。ギャンブル嗜好程度はγ-GTPに無関係と思われていたが関係性があるという結論になった

４．相関分析

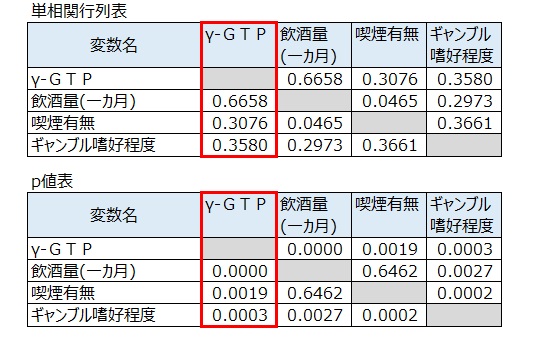
• 飲酒量とγ-GTPとの相関係数は0.6658(ｐ値<0.05)で、飲酒量はγ-GTPへの影響要因といえる。
• 喫煙有無はγ-GTPとの相関係数0.3076(p値<0.05)で、喫煙有無はγ-GTPへの影響要因といえる。
  ※喫煙有無は距離尺度でないが、「喫煙しない」を0点、「喫煙する」を1点として距離尺度に変換して相関係数を算出した。
• ギャンブル嗜好とγ-GTPとの相関係数は0.3580(ｐ値<0.05)で、ギャンブル嗜好はγ-GTPへの影響要因といえる。

５．見かけの相関、真の関係

相関関係を図で示す。

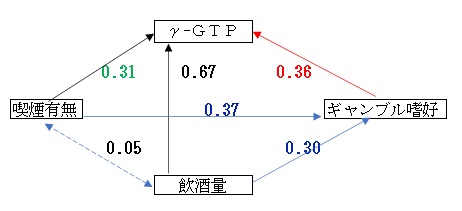
「γ-GTPとギャンブル嗜好」の相関は0.36、「γ-GTPと喫煙有無」は0.31で前者の方が高い。ギャンブル嗜好の方が喫煙有無より、γ-ＧＴＰに影響度が高いといえるだろうか？

「喫煙有無とギャンブル嗜好」の相関は0.37、「飲酒量とギャンブル嗜好」の相関は0.30でどちらも相関関係が見られ、喫煙する人ほど、飲酒量が多い人ほどギャンブル嗜好程度が高いといえる。ギャンブル好きだからγ-ＧＴＰが高いのではなく、ギャンブル好きは喫煙し、飲酒量が多いからγ-ＧＴＰが高いと推察できる。

「γ-GTPとギャンブル嗜好」の相関0.36は見かけの相関である。「γ-GTPとギャンブル嗜好」の真の関係は喫煙有無や飲酒量の影響を除去したものでなければならない。

このような真の関係を把握する方法として以下がある。

・重回帰分析
・傾向スコアマッチング分析

６．重回帰分析

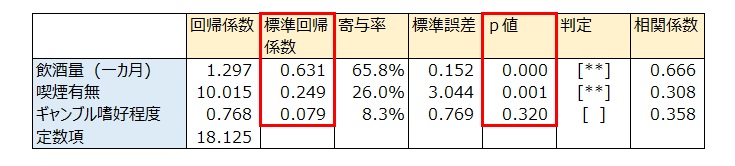
γ-GTPを目的変数、飲酒量・喫煙有無・ギャンブル嗜好程度を説明変数として重回帰分析を行った。

標準回帰係数を見ると、ギャンブル嗜好程度は0.079と小さく、またｐ値＝0.320＞0.05で、ギャンブル嗜好はγ-GTPへの影響要因でないといえる。

重回帰分析は、目的変数と説明変数の真の関係を明らかにする手法である。

７．傾向スコアマッチング分析とは

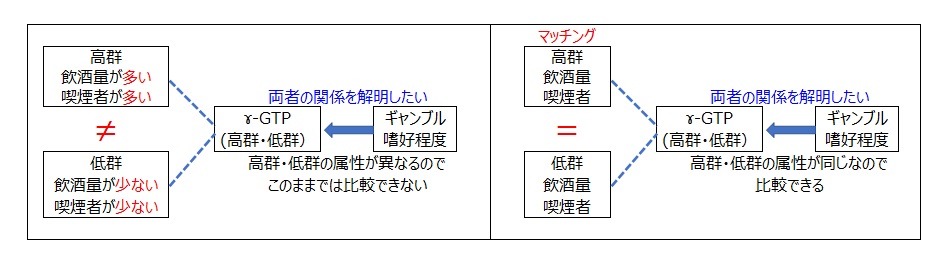
高群は飲酒量多者や喫煙者が多く、低群は飲酒量少者や非喫煙者が多い。このような状況でギャンブル嗜好程度の平均について高群と低群を比較すれば「ギャンブル嗜好と飲酒量や喫煙は相関関係がある」ので、ギャンブル嗜好程度は高群の方が低群より高くなるのは当然である。

ギャンブル嗜好程度の平均を高群と低群で比較する際、両群の飲酒量や喫煙有無が同等であれば真の比較ができる。すなわち、高群と低群で飲酒量や喫煙有無が似ているサンプルだけを取り出して比較すればよい。

具体的には両群から似ている要素をもつデータを見つけてペアにすることである。
※統計学において異なるサンプルで，似ている要素（交絡因子という）をもつデータを見つけてペアにすることをマッチングと言う。

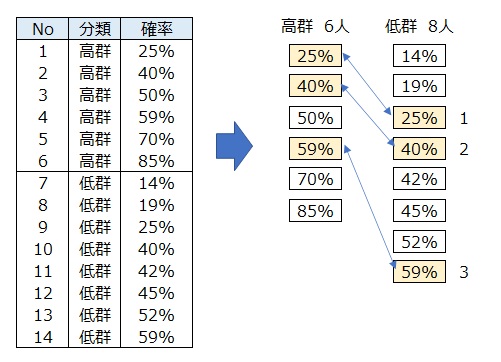
14人について、飲酒量・喫煙有無から各サンプルがγ-GTP高群となる確率を求めたとする。
両群から確率が似ている(同じ)サンプルを見つけてペアにする。
高群6人、低群8人においてペアは3人である。選ばれた3人は、「飲酒量・喫煙有無」の状況（傾向）が似ている人であるということになります。

確率を傾向スコアという。同じような傾向を持つ人をペアにする方法を傾向スコアマッチングと言う。

傾向スコアは，目的変数を高群＝1，低群＝0、説明変数を交絡因子である飲酒量、喫煙有無にしてロジスティック回帰を行うことで求められる。

ロジスティック回帰で導かれる各サンプルの判別スコアを傾向スコアとする。

マッチングされたペアデータについて、検証したい原因項目（具体例はギャンブル嗜好程度）と目的変数(γ-GTP)について相関検定や有意差検定を行う。

交絡因子の傾向スコアでマッチングしペアを見つけ、ペアデータについて目的変数と原因変数の関係を検証する方法を傾向スコアマッチング分析という。

８．ロジスティック回帰分析

ロジスティック回帰分析は目的変数が2群のカテゴリーデータ、説明変数が数量データとする多変量解析の手法である。

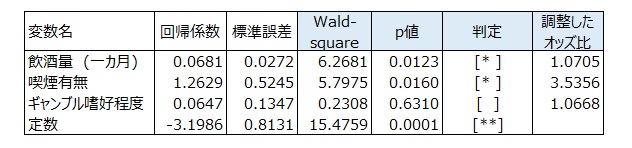
説明変数の目的変数に対する影響度を示すWald-squareを算出する。
各サンプルについて、2つの群A,BについてAとなる確率である「判別スコア」を算出する。

具体例について行うロジスティック回帰分析は2つある。

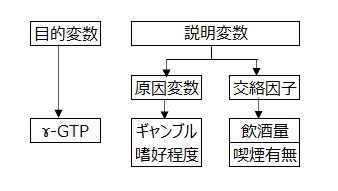
• 目的変数：γ-GTP　説明変数：交絡因子 ＆ 原因変数
• 目的変数：γ-GTP　説明変数：交絡因子

①-１．把握内容

γ-GTP高群・低群の判別に影響する要因を解明する

①-２．結果

• γ-GTPへの影響度をWald-squareでみると、1位は飲酒量、2位は喫煙有無である。
  
• ギャンブル嗜好程度のWald-squareは小さく、ｐ値＞0.05より、ギャンブル嗜好程度はγ-ＧＴＰへの影響要因でないといえる。

②-１．把握内容

ギャンブル嗜好程度とγ-GTPとの真の関係を明らかにしたい。

マッチングし両群の傾向が同じ（飲酒量、喫煙有無が同じ）サンプルのペアを作りたい。

②-２．結果

• Wald-square、ｐ値の出力結果は見なくてよい。
  
• 判別スコア（確率）が重要である。

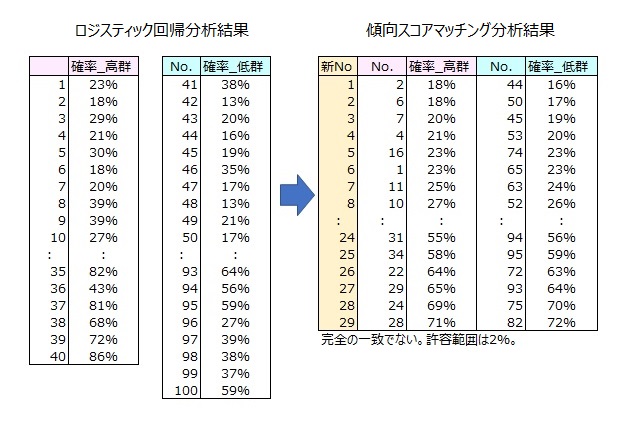
※マッチングには最近傍法、フルマッチング（完全に一致）がある。上記は最近傍法によるものである。

９．マッチング後の解析

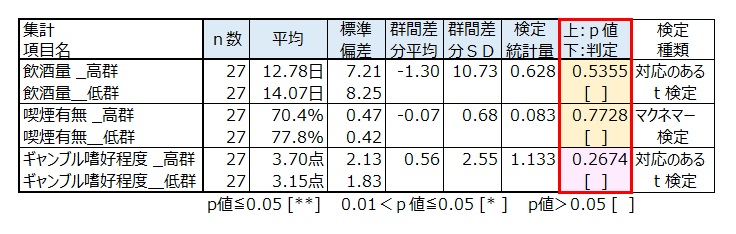
マッチング後のペアデータでγ-GTP2群間の有意差検定を行う。

γ-GTPの「50以上」を群1=高群、「49以下」を群2=低群とする。

• 飲酒量の平均は、高群14.03(日)、低群13.83(日)で高群が低群を0.2ポイント上回った。ｐ値0.9070＞0.05より高群は低群に比べ有意に高いといえない。
  このことから、マッチング後の飲酒量は高群・低群で同等である。
  
• 喫煙有無において「有り」の割合は、高群75.9％、低群79.3％で高群が低群を3.4ポイント下回った。ｐ値0.7055＞0.05より高群は低群に比べ有意に高いといえない。
  このことから、マッチング後の喫煙有無は高群・低群で同等である
  
• ギャンブル嗜好程度の平均は、高群3.52(点)、低群3.93(点)で高群が低群を0.41ポイント下回った。ｐ値0.3750＞0.05より高群は低群に比べ有意に高いといえない。
  マッチング前のギャンブル嗜好程度はγ-GTPに関係と思われていたが、このことから、関係性があるといえないことが検証できた。

マッチング後のサンプルサイズが30を下回る場合、母平均の有意差検定は、Ｕ検定を適用する。

この例題は30を下回ったのでＵ検定を行うのが正しいが省略する。