ロジスティック回帰分析 ≪ 1 / 3 ≫
ロジスティック回帰分析とは
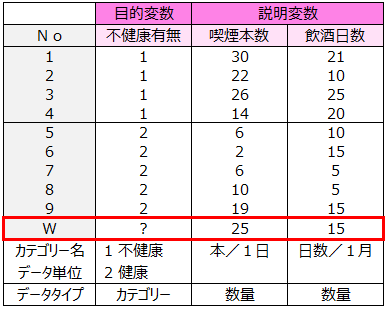
すでに確認されている「不健康」のグループと「健康」のグループそれぞれで、1日の喫煙本数と1ヵ月間の飲酒日数を調べました。下記に9人の調査結果を示しました。
下記データについて不健康有無と調査項目との関係を調べ、不健康であるかどうかを判別するモデル式を作ります。このモデル式を用い、1日の喫煙本数が25本、1ヵ月間の飲酒日数が15日であるWさんの不健康有無を判別します。
この問題を解いてくれるのがロジスティック回帰分析です。
予測したい変数、この例では不健康有無を目的変数といいます。
目的変数に影響を及ぼす変数、この例では喫煙有無本数と飲酒日数を説明変数といいます。
ロジスティック回帰分析で適用できるデータは、目的変数は2群のカテゴリーデータ、説明変数は数量データです。
ロジスティック回帰は、目的変数と説明変数の関係を関係式で表します。
この例題の関係式は、次となります。
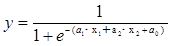

関係式におけるa1 、a2 を回帰係数、a0 を定数項といいます。
e は自然対数の底で、値は2.718 ・・・です。
ロジスティック回帰分析はこの関係式を用いて、次を明らかにする解析手法です。
① 予測値の算出
② 関係式に用いた説明変数の目的変数に対する貢献度
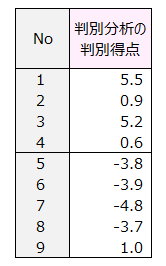
判別分析を行った結果を示します。
関数式:不健康有無=0.289×喫煙本数+0.210×飲酒日数-7.61
判別得点
判別分析は名前のとおり、2群を判別することを目的としており、説明変数の効果にはあまり注目しません。また、分析に利用する変数は正規分布にしたがう必要があります。一方、ロジスティック回帰分析も2群を判別することを目的としていますが判別分析と異なり、説明変数の効果に注目します。これはオッズ比(odds ratio)として知られる指標にもとづき、たとえば、「喫煙する人は喫煙しない人に対して、死亡のリスクが何倍になる」といったように、異なる条件間でのアウトカム(死亡、解約など)の発生要因を分析することができます。また、分析に使用する変数が正規分布にしたがう必要はありません。次の「判別スコア」で両者の解釈の違いを説明します。判別分析とロジスティック回帰分析には類似点もありますが、説明変数の評価を目的とする場合などは、判別分析よりロジスティック回帰分析を優先させたほうがよいでしょう。
判別スコア
関係式に説明変数のデータをインプットして求めた値を判別スコアといいます。
判別スコアの求め方をNo.1の人について示します。関係式にNo.1の喫煙本数、飲酒日数を代入します。
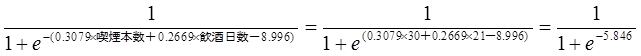

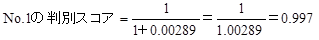
全ての人の判別スコアを求めます。
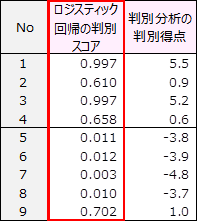
この例題に判別分析を行い、判別得点を算出しました。
両者の違いを調べてみます。
判別スコアは0~1の間の値で不健康となる確率を表します。
判別得点はおよそ-5~+5の間に収まる得点で、プラスは不健康、マイナスは健康であることを示しています。
健康群のNo.9の人について解釈してみます。
判別スコアは0.702で、健康群なのに不健康となる確率は70.2%でした。
判別得点は1.0で、健康群なのに不健康だと判定されます。
判別精度
ロジスティック回帰における判別精度は、判別的中率と相関比があります。
判別的中率
各個体について判別スコアが0.5より大きいか小さいかでどちらの群に属するかを調べます。 この結果を推定群、「不健康群と健康群」を実績群と呼ぶことにします。各個体の実績群と推定群を示します。
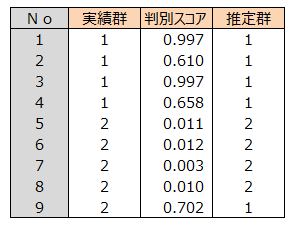
実績群と推定群とのクロス集計表(判別クロス集計表という)を作成し、 実績群と推定群が一致している度数、すなわち、「実績群1 かつ推定群1」の度数と「実績群2 かつ推定群2」の度数の和を調べます。 判別的中率はこの和の度数の全度数に占める割合で求められます。
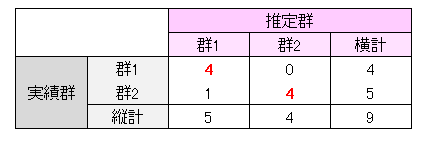
判別的中率は
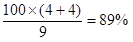
となります。
判別的中率はいくつ以上あればよいという統計学的基準は有りませんが、 著者は75 % 以上あれば関係式は予測に適用できると判断しています。

相関比
カテゴリーデータと数量的データの関連性を調べる解析手法として相関比があります。 群はカテゴリーデータ、サンプルスコアは数量的データなのでこの例題に相関比を適用すると、相関比は0.657でした。
相関比の求め方を示します。
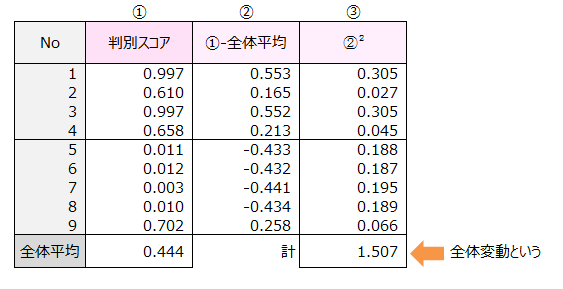
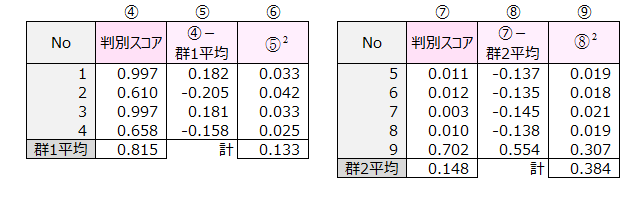
群内変動=⑥の計+⑨の計=0.133+0.384=0.517
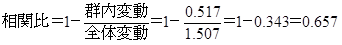
相関比は, 0~1 の値となります。 相関比は判別的中率同様に、いくつ以上あればよいという基準はありませんが、筆者は0.5 を基準の値としています。 この例題の相関比は0.657 で0.5を上回ったので、関係は予測に適用できると判断します。
予測
不健康有無の判別的中率は89%>75%、相関比は0.657>0.5より、関係式は予測に適用できると判断し、Wさんを予測します。予測するWさんは 喫煙本数は25本、飲酒日数は15日です。
Wさんの予測値は

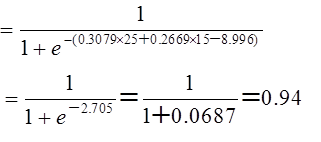
Wさんの不健康となる確率は94%です。
説明変数の選び方
ロジスティック回帰の説明変数は何でもよいということでありません。
説明変数の選び方にはルールがあります。そのルールについて説明します。
①選択肢が3つ以上のカテゴリーデータの項目は適用できない。
説明変数に適用できるデータは数量データです。
飲酒日数、喫煙本数、性別、血液型から不健康有無を予測したいと思います。
次の表のデータはロジスティック回帰に適用できるかを考えてみてくだい。
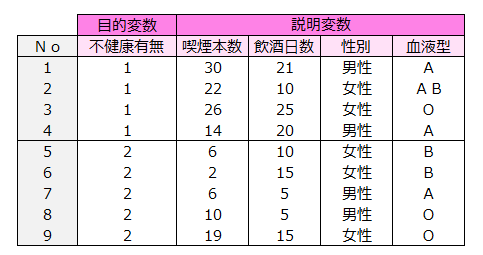
性別、血液型はカテゴリーデータなので、ロジスティック回帰には適用できません。
ただし、カテゴリー数が2つの項目は適用できます。
・性別:男性→1 女性→0 として、数量データとして扱えます。女性→1 男性→0でもよいです。
・血液型:4カテゴリーなので適用できません。
②データがすべて同じ値の説明変数は、判別分析に適用できない。
アンケート調査で得た段階評価(1.良い 2.どちらともいえない 3.悪い)のデータを用いる場合などに、全員が「2・どちらともいえない」に回答する、といったことがたまにあります。この場合、この変数のデータはすべて「2」となり、この変数はロジスティック回帰に使えません。データがすべて同じだと標準偏差が0になるので、ロジスティック回帰を行う前に標準偏差を計算してチェックして下さい。
③説明変数の個数は「個体数-1」より少なくなければならない。
説明変数の数をq、個体数をnとしたとき、ロジスティック回帰では次式を満たしてなければなりません。
q<n-1
不健康有無のデータの場合、n-1は9-1=8です。q=2なので、q<n-1が成立し、ロジスティック回帰は適用できます。この例においてnが3以下の場合だとロジスティック回帰は行えません。
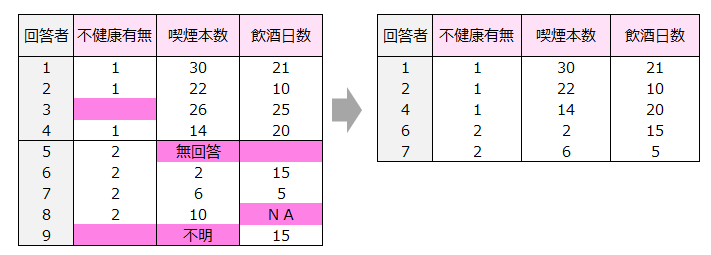
④数値以外のデータがある個体は分析から除外される。
ブランク、記号、文字などの数値以外のデータがある個体は分析から除外されます。
下記のデータの場合、個体数は9人ですが数値以外のデータがある個体数は4人存在するので、解析に適用できるデータは右表の5人となります。
ロジスティック回帰分析のオッズ比
ロジスティック回帰分析におけるオッズ比について説明します。
ロジスティック回帰のオッズ比は関係式の回帰係数から算出されます。
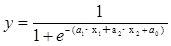
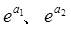
をオッズ比といいます。
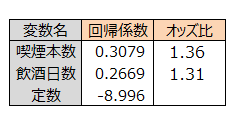

オッズ比は値が大きいほど、不健康になるリスクが高いといえます。
しかし、オッズ比から倍率の解釈はできません。
喫煙本数が1日に1本増えると、不健康になる確率が1.36倍になるという解釈はできません。
オッズ比が1を下回ることがあります。例えば、説明変数にウォーキング有無があり、オッズ比が0.8だとします。「不健康」になるオッズ比は0.8ですので、逆数(1÷0.8=1.25)を計算し、ウォーキングの「健康」になるオッズ比は1.25という解釈もできます。
不健康有無の喫煙本数を1,0データに変換し、喫煙分類のデータを作成します。
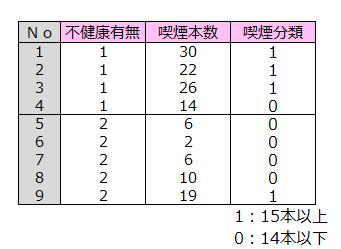
不健康有無を目的変数、喫煙分類を説明変数とするロジスティック回帰を行います。
オッズ比は12.00でした。
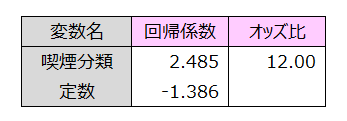
このデータのリスク比とオッズ比を計算します。
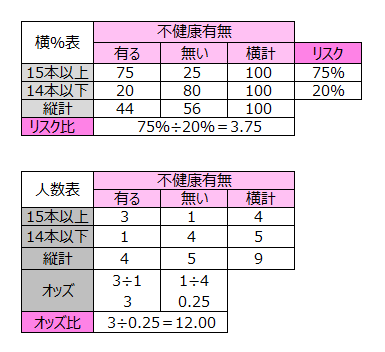
説明変数が1つの場合、ロジスティック回帰のオッズ比とクロス集計から算出されるオッズ比は一致します。
ロジスティック回帰の説明変数が2つ以上のオッズ比を「調整したオッズ比」、1つを単にオッズ比といいます。
