曲線回帰分析によるトレンド予測 ≪2/4≫
解析手法「直線回帰式」の役割
直線回帰式は、売上(TC)について直線のトレンドT(傾向線)を算出します。
適用できるデータ形態と時期数
月次データ、四半期データ、年次データ、日別データなど全ての時間変数に適用できます。
データの時期数はどのデータ形態も4以上です。
<具体例> 下記表は売上のTCデータです。

直線回帰式とトレンドTについて
具体例のデータで、売上のTCをy、年をxとして、直線回帰分析を行いました。
ただし年は西暦年でなく、1,2,3,4,5の整数とします。 直線回帰式は次となります。
y=2.1x+3.7
この式に、xの値1,2,3,4,5を代入し、yの値を求めます。この値がトレンドTです。
【例】 x=1の場合 y=2.1×1+3.7=5.8
全ての年について求めると次となります。
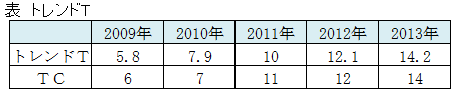
直線回帰式からわかること
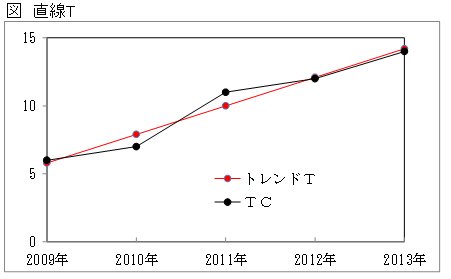
トレンドTとTCの折れ線グラフを描きます。
売上の変化は直線的な傾向で推移していることがわかりました。
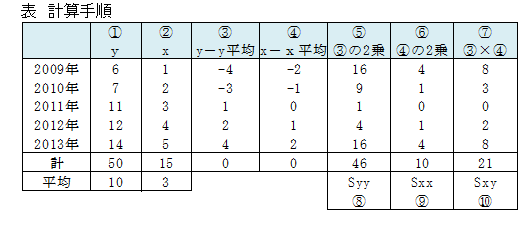
直線回帰式の求め方
直線回帰式のa、bは次の計算手順で求めることができます。
① yの平均を求める。
② xの平均を求める。
③ yの個々データ からyの平均 を引く。
④ xの個々データ からxの平均 を引く。
⑤ ③の2乗を求める。
⑥ ④の2乗を求める。
⑦ ③と④を掛ける。
⑧ ⑤の合計を求める。合計をSyy とする。
Syy をyの偏差平方和という。
⑨ ⑥の合計を求める。合計をSxx とする。
Sxx をxの偏差平方和という。
⑩ ⑦の合計を求める。合計をSxy とする。
Sxy を積和という。

決定係数(当てはまりの良さを調べる指標)
直線回帰式より求められたトレンドTとTCの値が近いほど、直線式の当てはまりが良いといえます。当てはまりの良さはTCとトレンドTの単相関係数で把握できます。
TCとトレンドTの単相関係数を求めると0.97913となります。単相関係数の2乗を決定係数といい、当てはまりの良さを調べる指標とします。
決定係数 = 0.979132 =0.9587 【計算例】 Excel関数 決定係数 ➡ =0.97913^2
決定係数は0から1の間の数値で、値が大きいほど当てはまりが良いといえます。
決定係数がいくつ以上あればよいという統計学的基準はありませんが、本解説では0.5未満のトレンドTは用いないことにしています。
トレンドTの予測
予測したい年のxの値を調べます。
開始年は必ず x=1としますので、予測したい年が2014年であれば2014年のx=6となります。
直線回帰式に、x=6を代入することによって、2014年のトレンドTを予測できます。
2014年のトレンドTの予測
y=2.1x+3.7 y=2.1×6+3.7=16.3
<留意点> 「最小2乗法」という統計学の話
少し難しいのですが、直線を求める公式がどのような考え方で作られたかを説明します。
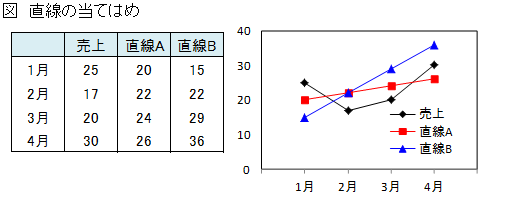
売上に2本の直線を当てはめました。
直線AとBではどちらの方が当てはまりがよいと判断できるでしょうか。
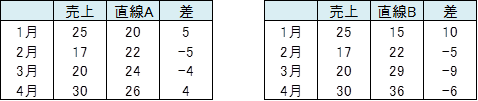
このことを明らかにするために、個々の月について売上と直線との差を調べてみました。
当てはまりの良い直線は、差がどの月についても小さいものであると考えます。
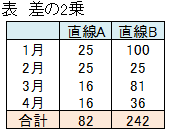
差(距離)を扱う場合、全てプラスの数値でみる必要性から、データを2乗することが良くあります。ここでも同様に、差の2乗をしてみます。
合計を比べると、直線Aの方が小さい値になっています。この値が小さいほど、当てはまりの良い直線だと考えられることができます。この例では、直線Bより直線Aの方が当てはまりが良いといえるのですが、もしかしたら、他に直線Aよりもさらに当てはまりの良い直線があるかもしれません。
合計を最小にするようなa、bを求めれば、最も当てはまりの良い直線の式が求められます。このような方法で、a、bを求める方法を「最小2乗法」といいます。先の係数を求める公式は、最小2乗法によって導かれたものです。