目次
曲線回帰分析によるトレンド予測 ≪4/4≫
解析手法「自然対数回帰式」の役割
自然対数回帰式は、売上(TC)について緩やかな増加傾向(減少傾向)を示すトレンドTを算出します。
適用できるデータ形態と時期数
月次データ、四半期データ、年次データ、日別データなど全ての時間変数に適用できます。
データの時期数はどのデータ形態も4以上です。
<具体例> 下記表は売上のTCデータです。

自然対数回帰式とトレンドTについて
具体例のデータで、売上のTCをy、年をxとして、自然対数回帰分析を行いました。
ただし年は西暦年でなく、1,2,3,4,5の整数とします。
自然対数回帰式は次となります。
y=alogx +b
y=5.0941× +5.1224
この式に、xの値1,2,3,4,5を代入し、yの値を求めます。この値がトレンドTです。
【例】 x=4の場合 y=5.0941×log (4)+5.1224=12.18
全ての年について求めると次となります。
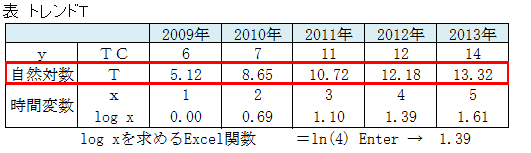
自然対数回帰式からわかること
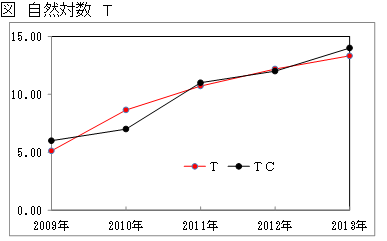
トレンドTとTCの折れ線グラフを描きます。
売上の変化は緩やかな上昇基調で推移していることがわかりました。
自然対数回帰式の求め方
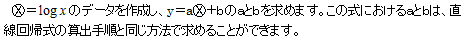
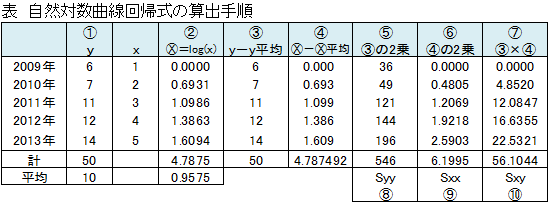
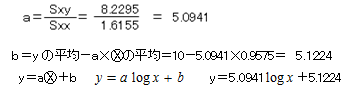
決定係数(当てはまりの良さを調べる指標)
自然対数回帰式より求められたトレンドTとTCの値が近いほど、曲線式の当てはまりが良いといえます。当てはまりの良さは、TCとトレンドTの単相関係数で把握できます。TCとトレンドTの単相関係数を求めると0.9546となります。単相関係数の2乗を決定係数といい、当てはまりの良さを調べる指標とします。
決定係数を求めると0.9114です。

決定係数は0から1の間の数値で、値が大きいほど当てはまりが良いといえます。決定係数がいくつ以上あれば良いという統計学的基準はありませんが、本解説では決定係数が0.5未満のトレンドTは用いないことにします。



