相関比
相関比とは
相関比は「数量データ」と「カテゴリデータ」の関係を明らかにする統計手法です。
次の表は年令と好きな商品を調べたアンケート結果です。
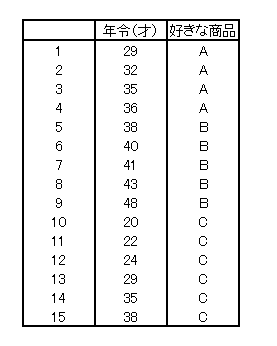
上記データから年令の違いによって、商品の好みは異なるといえるかを調べることにします。
このテーマに対する基本的分析方法は、好きな商品別の平均年令を算出することです。(この平均をカテゴリ別平均という)
カテゴリ別平均を求めてみます。平均は次表のよう、データを並べかえることによって簡単に計算できます。
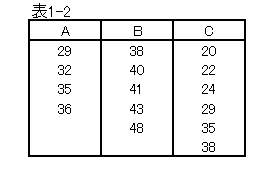
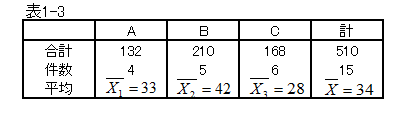
カテゴリ別平均をみると、商品別の平均年令に差がみられ、年令の違いによって商品の好みは異なるといえます。
カテゴリ別平均に差があるので、商品と年令には関連があるといえます。関連があるのは分かりましたが、関連の強弱までは分かりません。そこで、年令と好きな商品の相関を求めることにします。もし、相関があれば、「年令の違いによって商品の好みに違いがある」ということが言え、相関の値から「違い」の強弱が分かります。
ここでの相関は、年令は数量データ、好きな商品はカテゴリデータなので相関比を用いることになります。
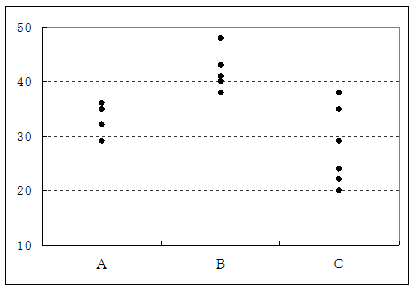
商品ごとの年令幅をみると、A商品志向グループは29~36才、B商品志向グループは38~48才、C商品志向グループは20~38才と年令幅に違いがみられます。
カテゴリ別平均値に大きな差があるほど、商品と年令は関連があると述べました。表1-4では、年令幅に違いがあるとき関連があると考えます。それでは、年令幅がどのような時、最も関連が「ある」あるいは「ない」かを調べてみます。
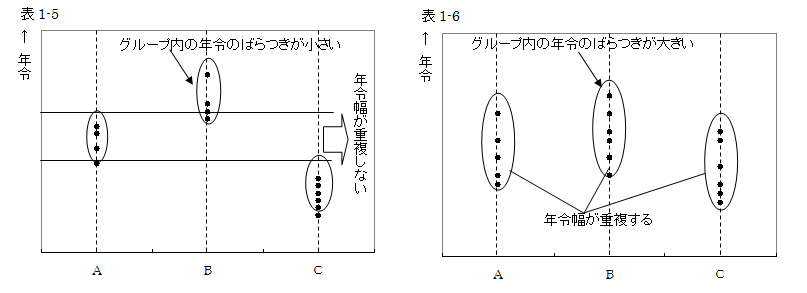
表1-5のように、グループ内の年令のばらつきが小さく、年令幅が重複しないとき、商品と年令の関係は強いと考えます。
表1-6のように、グループ内の年令のばらつきが大きく、年令幅が重複するとき、商品と年令の関係は弱いと考えます。
級内変動
表1-2について、グループ内のばらつきを計算してみます。ばらつきは偏差平方和を用います。
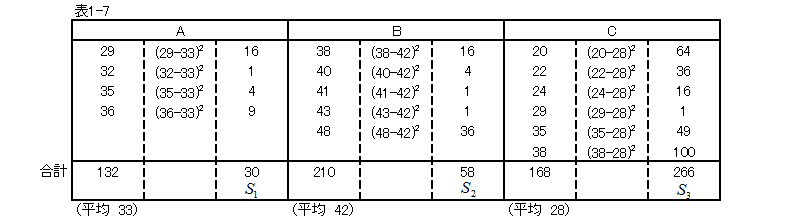
3つの偏差平方和を合計したものを級内変動といい、Swで表します。
Sw=S1+S2+S3=354・・・・
級間変動
グループの平均を計算し、3つの平均のばらつきを算出します。年令幅が重複しないということは、3つの平均のばらつきが大きいことを、逆に年令幅が重複するということは、3つの平均のばらつきが小さいことを意味します。
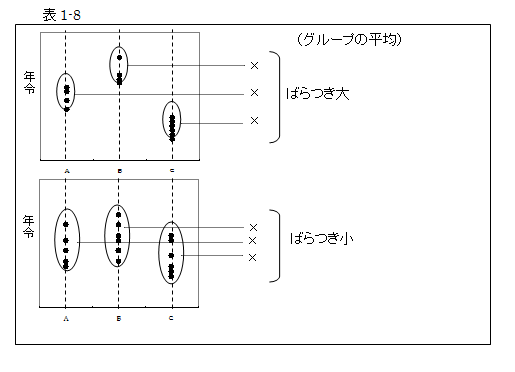
年令幅のばらつき、すなわちグループ間のばらつきは、各グループの平均と全体平均との差から求められ、これを級間変動といい、SB で表します。

いままでの説明でお分かりのように、級内変動が小さく、級間変動が大きいとき関連があると判断します。
そこで、2つの変動合計に対する級間変動の割合を求めます。これを相関比といい、η2(イータ2乗_と読む)で表します。
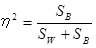
この式をみると、最も関連が強いとき、級内変動( Sw )は「0」、すなわちグループ内に属するデータが全て同じになり、η2は「1」になります。
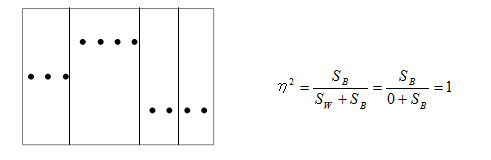
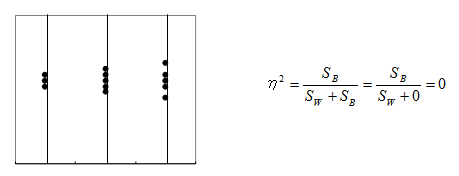
逆に、最も関連が弱いとき、級間変動(SB )は「0」、すなわちグループ平均が全て同じになり、η2は「0」になります。
ここで、表1-1の全体の偏差平方和を求めてみます。

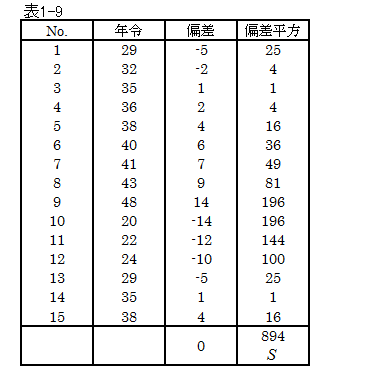
偏差平方和 S は894となります。SW は354、SB は540です。これらをくわえるとS に一致します。
S = SW + SB
この例だけでなくどんな場合も一致します。したがって相関比η2は、次の公式となります。
相関比はいくつ以上あればよいか
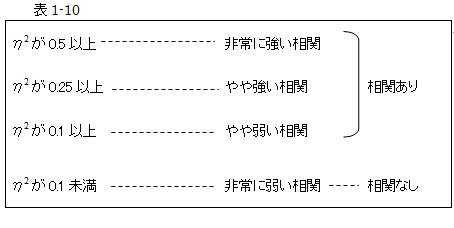
相関比は0から1の間をとり、1に近づくほど、2変数は相関関係があることが分かりました。
それでは、η2(相関比)が、いくつ以上あれば相関関係があるといえるのでしょうか。
単相関同様、基準はありません。著者は次のように定めています。