単相関係数
単相関係数とは
単相関係数は「数量データ」と「数量データ」の関係を明らかにする統計手法です。
「店舗前通行人が多いほど日販は高くなるといえるか」を明らかにするために、単相関係数、散布図(相関図ともいう)を適用します。
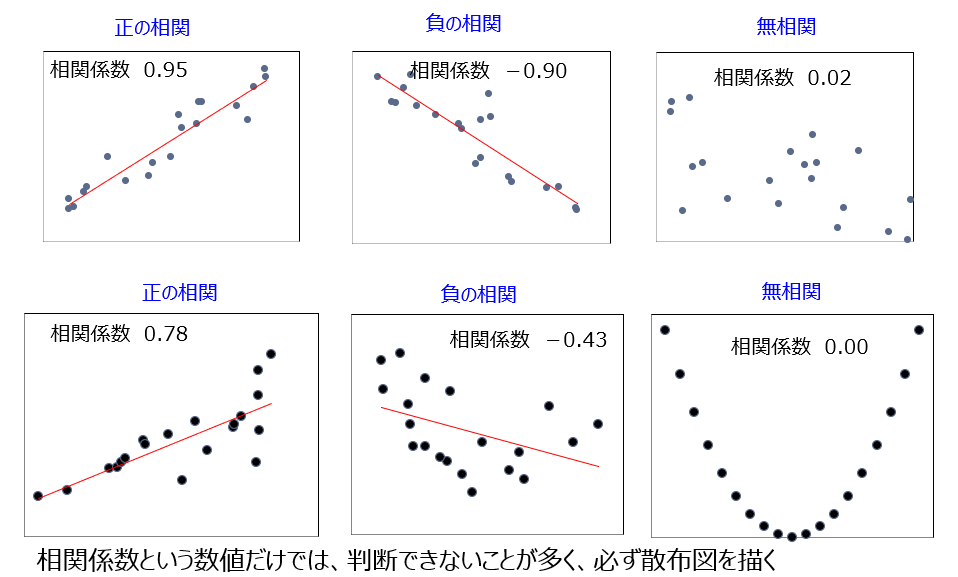
散布図をみると、通行人の値が決まれば日販の値が決まるというわけではありませんが、両者の間に直線的な関連性が認められます。このような関係がみられるとき、「通行人と日販との間には相関関係がある」といい、相関関係の程度を示す数値が単相関係数となります。
単相関係数は、-1から+1までの値をとります。単相関係数が±1に近いときは2つの変数の関係は直線的であって、±1から遠ざかるに従って直線的関係は薄れていき、0に近いときは変数の間にまったく直線的な関係はありません。
単相関係数でわかることは「直線的関係の有無」であって、例えば放物線のような曲線的関係があるかないかなどについては触れていません。例えばD図のような場合、直線的関係がないので相関関係はありません。しかし、全く関係がないともいえません。このような直線的でない2つの変数の関係を見ようとする場合は、単相関係数とは異なる尺度を用いなければなりません。
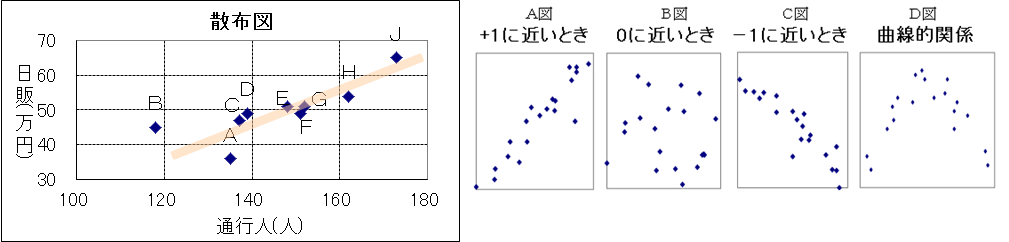
散布点の位置がどのようなとき相関関係が強いか
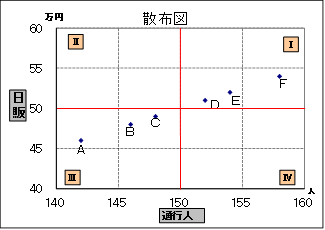
「店舗前通行人と日販」のデータについて、散布点の位置がどのようなとき相関関係が強いかを考えてみましょう。
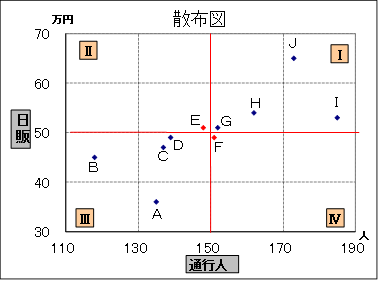
日販と通行人の平均を計算すると、それぞれ50万円、150人になります。散布図に日販の平均を横線で、通行人の平均を縦線で描き加えたものが下の図です。
平均線で分けられた4つの領域を、図に示すようにⅠ~Ⅳとします。
グラフの横軸項目を変数x、縦軸項目を変数yと名称します。
変数xと変数yが無関係であるならば、点は4つの領域ⅠからⅣに均等にばらついて存在します。xとyの間に相関がありxが増加するとyも増加する傾向がある場合は、点は領域ⅠとⅢは特に多く、ⅡとⅣに少なくなります。逆にxが増加するy が減少する傾向がある場合は、ⅡとⅣ多く、ⅠとⅢに少なくなります。
この散布図では、領域ⅠとⅢに点が多く、ⅡとⅣにそれぞれ1つずつしか点が存在しないので、通行人(変数x)と日販(変数y)の間には相関関係が強いと推測することができます。
相関係数の強さを表す「積和」
日販と通行人のデータについて、どの程度の相関があるかを数値で表す方法を考えてみましょう。
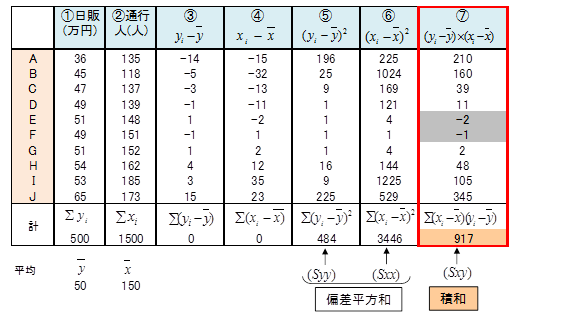
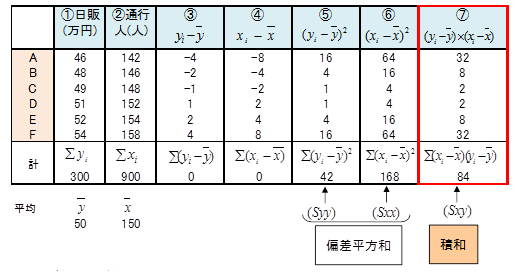
日販と通行人のデータ表について測定値から平均値を引いた値(偏差という)を求めて下表の③④に記入します。
③を平方し⑤に記入、④を平方し⑥に記入します。
⑤の合計を日販 の偏差平方和といい、 Syy で表します。
同様に⑥の合計を通行人の偏差平方和といい、Sxx で表します。
次に、③と④とを掛算し⑦に記入します。⑦の合計を積和といい、Sxy で表します。
⑦列のデータを見るとEとFの値は負(マイナス)で、積和の値を小さくする要因になっています。このEとFを散布図でみると、領域ⅡとⅣの場所にあります。いま仮に、EとFが領域ⅠとⅢの範囲にあれば、そのときの偏差の積も正(プラス)の値になり、積和( Sxy )はさらに大きくなります。同時に、点の分布もさらに右上がりの直線的な傾向を示すようになります。このことから、積和の値が大きければ相関関係が強くなることがわかります。
単相関係数の公式
極端な例として、下図のように通行人と日販の関係が1つの直線の上に乗っている場合の積和を計算してみましょう。
この例は、相関関係がいちばん強いときの関係にあたります。ということは、この例から導き出される相関係数が1.00になるように考えていけばよいわけです。
おもしろいことに、相関関係がいちばん強いときの状態で、積和( Sxy )を「x の偏差平方和( Sxx )とy の偏差平方和( Syy )の積の平方根」で割ると、1.00になります。上記の表からこのことを確かめてみましょう。
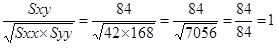
このことからわかるように、単相関係数は、「積和」を「x の偏差平方和とy の偏差平方和の積の平方根」で割ることによって求めることができます。
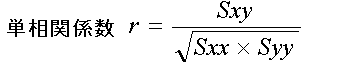
日販と通行人の単相関係数
日販と通行人の単相関係数を求めると、0.710となります。
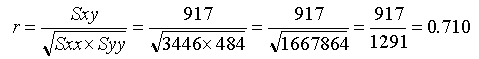
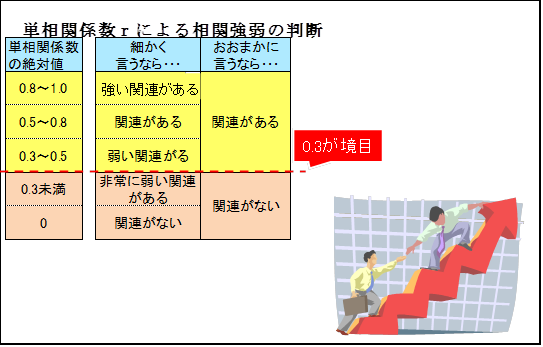
単相関係数はいくつ以上あればよいか
相関係数の値が±1近づくと相関関係が強くなり、反対に0に近づくと弱くなります。相関係数が0の場合のみ相関関係がありません。ちょっと信じられないかもしれませんが、相関係数がわずか0.1でも相関は弱いながらあるのです。したがって大概の場合、2変数の間には強弱の違いはありますが、相関関係がみられます。このことから、大事なのは強い相関があるかどうかです。ところが、いくつ以上あれば相関が強いといった、統計学的基準はありません。この基準は、分析者が経験的な判断から決めることになります。先生のノウハウとして、下表のように決めています。
ある会社では毎月、売上額と広告費と単相関係数を算出しています。6ヶ月ほど前まで相関係数は0.3~0.8の間で推移していましたが、それ以降は0.3を1度も上回ったことがありません。相関係数が基準点の0.3を上回らないのは広告費の売上に対する影響度が小さくなったと判断し、広告費の削減、あるいは広告内容の見直しを検討します。
基準点0.3はマーケティング施策等の意思決定をするときに用いています。この値も統計学的基準でなく先生のノウハウ値です。
色々な散布図の相関係数