傾向スコアマッチング・IPW(プロペンシティスコア)とは
共分散分析と同じように共変量 (交絡因子とも言う)の影響を取り除いて、母平均の差の検定を行う解析手法です。共変量の個数は共分散分析が1つであるのに対し、当解析手法は複数個適用できます。
ロジスティック回帰分析より算出される傾向スコア(確率)を適用して共変量の影響を除去します。
「傾向スコアマッチング・IPW」と「共分散分析」の違い
二つの会社(2群)の平均年収の差を把握したいというテーマがあります。
A社とB社の平均年収の差は、「本当にその会社の給与水準(平均年収)が高いのか」、「その会社の従業員は年齢が高い人が多くいて、年齢に引っ張られて平均年収が高くなっているのか」、真実はわかりません。このテーマを解決したい場合、共分散分析を適用します。共分散分析は「年収に影響を与えていると考えられる年齢の影響を除いたA社とB社の比較ができる」解析手法です。
共分散分析で取り扱える共変量(交絡因子ともう言う)は一つです。
このテーマの調べたい変数は年収、共変量は年齢ですが、仮にこのテーマの共変量に性別が追加された場合、共分散分析では年齢、性別の影響を除去して二つの会社の平均年収の差を把握することはできません。
共変量の個数が複数あるとき、共変量の影響を除去して調べたい変数の2群の平均を比較することができる解析方法は傾向スコアマッチング・IPW(プロペンシティスコア)となります。
また、適用できるデータは、共分散分析が数量データしか適用できないのに対して、傾向スコアマッチング・IPW(プロペンシティスコア)は、数量データに加え、性別などのカテゴリーデータも適用可です。
多数の共変量の影響を除去して、2群の平均を比較する解析手法
健康診断の検査値γ-GTP(ガンマジーティーピー)と飲酒量、喫煙有無とは相関関係があることが知られています。γ-GTPが高い群と低い群でギャンブル嗜好程度の平均を比較したら、高群の方が低群に比べ平均が高くなりました。この現象をそのまま信じてよいでしょうか。
この現象はギャンブル嗜好程度の高い人ほど飲酒、喫煙の量が多いことが起因しています。ギャンブル好きだからγ-GTPが高いのではなく、ギャンブル好きは喫煙し、飲酒量が多いからγ-GTPが高いと推察できます。
したがってγ-GTP高群、低群のギャンブル嗜好程度の平均を調べる際、ギャンブル嗜好程度に影響する共変量(飲酒量、喫煙有無)の影響を除去してから平均を比較しなければなりません。このことを解決してくれる解析手法に傾向スコアマッチングとIPW(プロペンシティスコア)があります。
<具体例>
健康診断の検査値の一つにγ-GTP(ガンマジーティーピー)があります。γ-GTPは肝臓や胆管の細胞がどれくらい壊れたかを示す指標で、検査値が成人男性の場合100(基準は50)を超えると、肝硬変、肝がん、脂肪肝、胆道疾患の可能性があるといわれています。
γ-GTPが高くなる理由は色々と考えられます。例えば、飲酒量、喫煙有無です。もしかしたらギャンブル嗜好程度が影響しているかもしれません。
そこで、100人の成人男性について、γ-GTP、飲酒量(一カ月に飲酒する日数)、喫煙有無、ギャンブル嗜好(7件法)を調査しました。
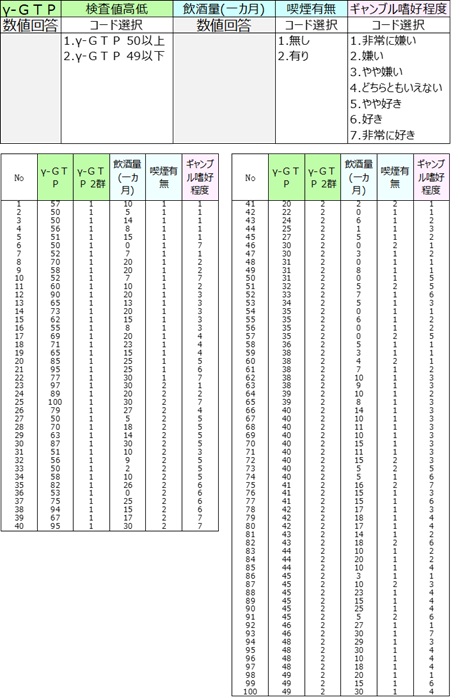
γ-GTPとの相関係数を算出しました。
| 変数名 | γ-GTP |
|---|---|
| 飲酒量(一カ月) | 0.6658 |
| 喫煙有無 | 0.3076 |
| ギャンブル嗜好程度 | 0.3580 |
ギャンブル嗜好程度とγ-GTPとの相関は0.3580と飲酒量に続く値を示しました。
飲酒や喫煙がγ-GTPに影響しているのは理解できますが、ギャンブルがγ-GTPに影響していることを疑わしく思われます。
そこで4変数相互の相関係数を算出し相関図を描いてみました。
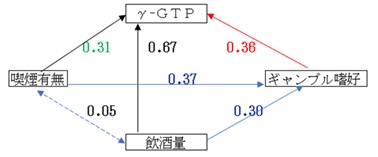
「喫煙有無とギャンブル嗜好」の相関は0.37、「飲酒量とギャンブル嗜好」の相関は0.30で、どちらも相関関係が見られ、喫煙する人ほど、飲酒量が多い人ほどギャンブル嗜好程度が高いといえます。
ギャンブル好きだからγ-GTPが高いのではなく、ギャンブル好きは喫煙し、飲酒量が多いからγ-GTPが高いと推察できます。「γ-GTPとギャンブル嗜好」の相関0.36は見かけの相関です。「γ-GTPとギャンブル嗜好」の真の関係は喫煙有無や飲酒量の影響を除去したものでなければなりません。このような真の関係を把握する方法に、傾向スコアマッチング・IPWがあります。
傾向スコアマッチング・IPWは2群変数、調べたい変数、共変量のデータを解析する手法です。
γ-GTPは数量データなのでγ-GTPが高い/低いの2群にします。
ここではギャンブル嗜好のγ-GTPへの真の影響度を知りたいのでギャンブル嗜好が調べたい変数です。
飲酒量、喫煙有無の影響を除去して解析するので、飲酒量、喫煙有無が共変量となります。

傾向スコアマッチングの場合、共変量が同じような傾向を持つ人をペアにしたデータで、2群の平均を比較する解析手法です。



IPW(逆数重みづけ法とも言う)の場合、個体数を減らさずにすべての個体のデータで求めた共変量調整済み平均を使って、2群の平均を比較する解析手法です。
傾向スコアマッチングの事例
具体例のデータについて、γ-GTP高群、低群別の平均を算出しました。
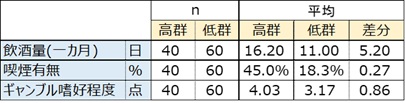

平均値から、γ-GTPの高群は飲酒量多者や喫煙者が多く、低群は飲酒量少者や非喫煙者が多いことが分かります。このような状況でギャンブル嗜好程度の平均について高群と低群を比較すると、ギャンブル嗜好と飲酒量との相関、ギャンブル嗜好と喫煙有無との相関が高いことから、ギャンブル嗜好程度は高群の方が低群より高くなるのは当然です。
γ-GTP高群と低群でギャンブル嗜好程度の平均を比較する際、両群の飲酒量や喫煙有無が同等であれば真の比較ができます。すなわち、高群と低群で飲酒量や喫煙有無が似ているサンプルだけを取り出して比較すればよいのです。
具体的には両群から共変量(飲酒量、喫煙有無)の傾向が似ているサンプルを見つけてペアにすることです。
同じような傾向を持つ人をペアにする方法を傾向スコアマッチングといいます。
具体例の100人のデータでなく、説明しやすい14人のデータを使って説明します。
- 共変量である飲酒量、喫煙有無を用いて、各サンプルがγ-GTP高群となる確率を求めます。
- 両群から確率が似ている(同じ)サンプルを見つけてペアにします。
- 高群6人、低群8人においてペアは3組です。選ばれた両群の3人は、「飲酒量、喫煙有無」の状況(傾向)が似ている人です。
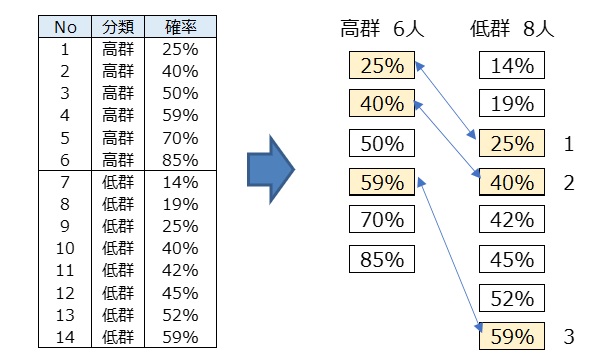

確率を傾向スコアといいます。
同じような傾向を持つ人をペアにする方法を傾向スコアマッチングといいます。
傾向スコアは、目的変数を高群=1,低群=0、説明変数を飲酒量、喫煙有無としてロジスティック回帰を行うことで求められます。ロジスティック回帰で導かれる各サンプルの確率を傾向スコアとします。



傾向スコアマッチングを実際にやってみましょう
① 具体例(100人データ)について、ロジスティック回帰分析を行います。
ロジスティック回帰分析は、目的変数が2群のカテゴリーデータ、説明変数が数量データとする多変量解析の手法です。カテゴリーデータはダミー変換して1点、0点とします。
目的変数:γ-GTP高群、低群
説明変数(共変量):飲酒量、喫煙有無
調整済みオッズ比、Wald-square、p値の出力結果は使用しません。
② 傾向スコア(確率)を使用します。
③ 傾向スコアが類似している人をペアにしました。
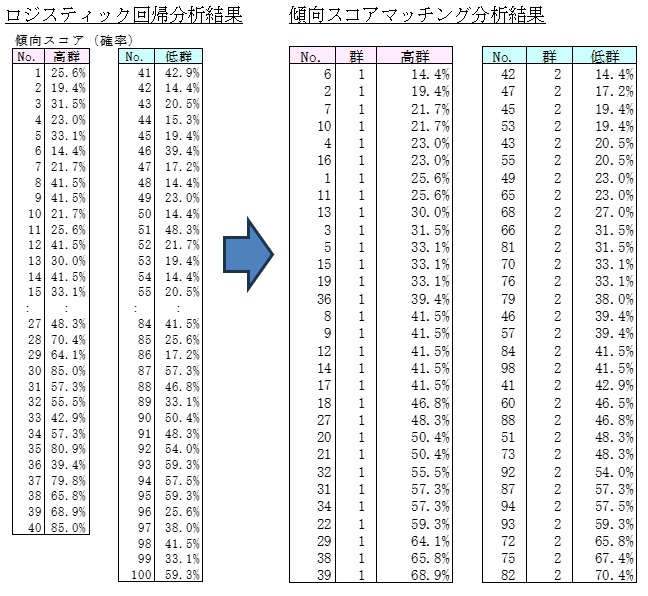

※ マッチングの方法には最近傍法、フルマッチング(完全に一致)があります。上記は最近傍法によるものです。
※ 一致させる許容範囲Caliper 係数(キャリパー)は3%としました。
(例)高群No2は19.4%、低群No47は17.2%で一致していないが、許容範囲3%以内のためマッチング
【留意点】
キャリパーの値を小さくするとマッチングできる人数が少なくなります。
マッチングできた人数を見て、キャリパーの数値を任意に変更します。
④ 「マッチング前」と「マッチング後」の解析結果を比較します。
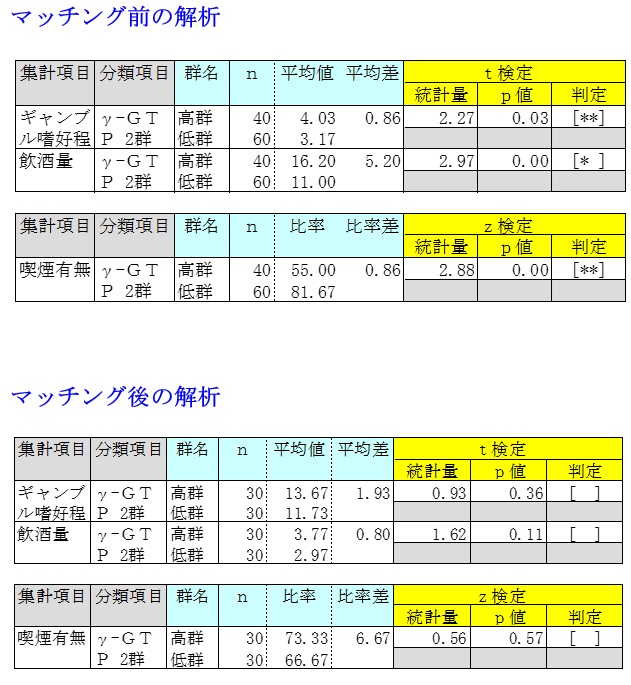

- γ-GTP高群と低群で調べたい変数「ギャンブル嗜好程度」の母平均の有意差を調べるt検定をしました。 → 有意差が見られました。
- γ-GTP高群と低群で共変量「飲酒量」の母平均の有意差を調べるt検定をしました。→ 有意差が見られました。
- γ-GTP高群と低群で共変量「喫煙有無」の母平均の有意差を調べるz検定をしました。→ 有意差が見られました。
- γ-GTP高群と低群で調べたい変数「ギャンブル嗜好程度」の母平均の有意差を調べるt検定をしました。→ 有意差が見られません。
- γ-GTP高群と低群で共変量「飲酒量」の母平均の有意差を調べるt検定をしました。→ 有意差が見られません。
- γ-GTP高群と低群で共変量「喫煙有無」の母平均の有意差を調べるz検定をしました。→ 有意差が見られません。
結論
Q.
γ-GTPが高い群と低い群でギャンブル嗜好程度の平均を比較したら、高群の方が低群に比べ平均が高く、有意差が見られました。この現象をそのまま信じてよいでしょうか。
A.
傾向スコアマッチングの結果より、「γ-GTPの高低にギャンブル嗜好は影響していない」といえます。
IPWの事例
γ-GTP高群と低群の個体数は40人と60人でした。傾向スコアマッチングを行うと個体数は高群30人、低群30人と減少しました。個体数が小さくなると正しい有意差判定が行えません。個体数を減らさずに2群を比較することのできる解析方法があります。それがIPW(プロペンシティスコア)です。逆数重みづけ法ともいわれます。
傾向スコアをロジスティック回帰によって求めるところまでは先に解説した傾向スコアマッチングと同じです。
傾向スコアは2群の判別の影響度(γ-GTP高群あるいは低群となる確率)を測る尺度です。傾向スコア(確率)は次表に示すように高群は低群より高い値となります。
両群の傾向スコアの差を小さくするために次式の逆数Weightを算出します。
① Weight
高群の個体 1÷傾向スコア
【例】個体No1 ➡ (1÷0.256)/2=1.951
低群の個体 1÷(1-傾向スコア)
【例】個体No41➡ (1÷(1-0.429))/2=0.876
② Weightの群別合計
高群 50.6 低群 48.6
各々の合計が群別合計(高群40人、低群60人)に一致するように、各個体のWeightを調整します。
この値を調整Weightといいます。
③ 調整Weightの計算方法
次式によって係数を算出します。
高群 50.6 → 40人 → 40÷50.6=0.790
低群 48.6 → 60人 → 60÷48.6=1.235
調整WeightはWeightに係数を掛けて求めます。
【例】個体No1
Weight 1.951×高群係数0.790=1.542
【例】個体No41
Weight 0.876×低群係数1.235=1.082
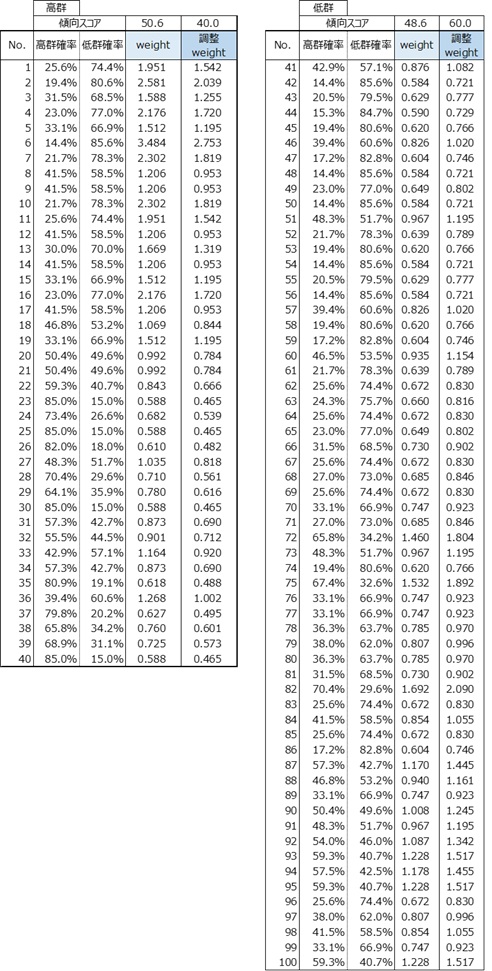

④ ウエイト集計
個々のサンプルの回答データに調整ウエイトを掛けた値を合計し、群人数で割ることによって、群別の平均や比率を算出します。
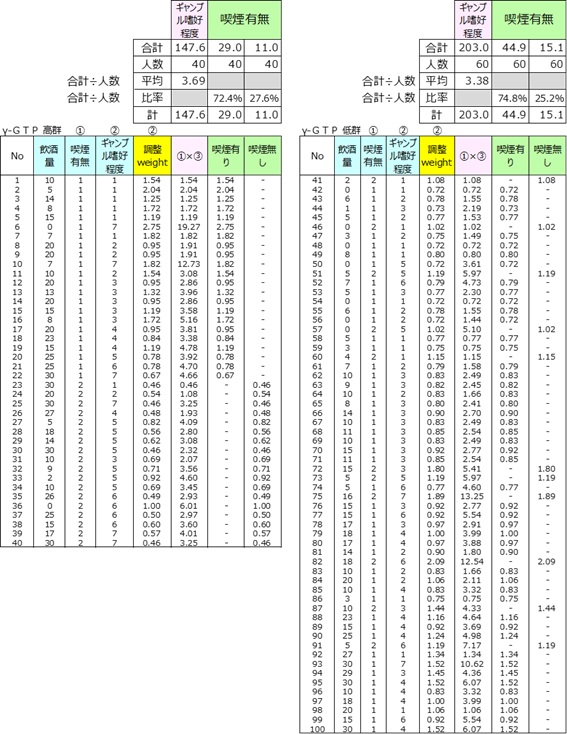

⑤ 2群の共変量調整済み平均を比較
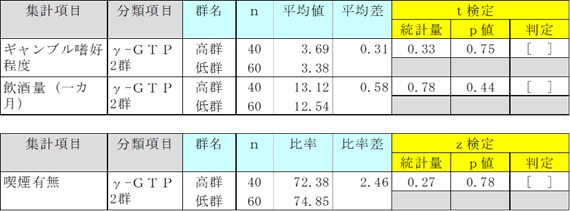

共変量である飲酒量、喫煙有無について、γ-GTP高群と低群では有意差がありませんでした。
2群の共変量は同じとなり、この2群でのギャンブル嗜好程度の比較は飲酒量、喫煙有無の影響を除去したもので、真の有意差検定ができます。
γ-GTP高群と低群のギャンブル嗜好程度平均の比較をt検定で調べました。
p値=0.75>0.05より、ギャンブル嗜好程度平均は高群、低群で有意な差が見られませんでした。
結論
IPWの結果より「γ-GTPの高低にギャンブル嗜好は影響していない」といえます。

