経時データ分散分析
はじめに
経時データとはn個の個体(被験者)の各々について、p個の時点で繰り返し測定されているデータのことである。(例:臨床試験データ,成長データ,教育・社会データ,経済データなど)
群別の有意差を検証する場合、群データの1列含め、総称して経時データという。
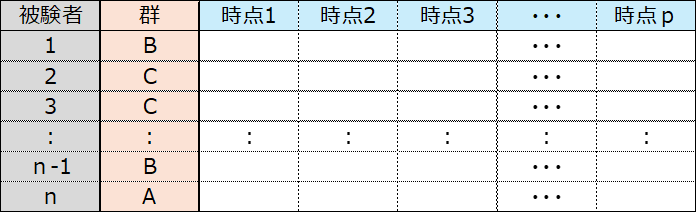
注. 上記表形式の経時データをバランス型経時データ(対応のある経時データ)という。
バランス型経時データは、欠損値(不明データ)があってはいけない。欠損値がある場合、その被験者を外して解析する必要がある。もしくは欠損値を推定して解析する。
経時データの分析方法として多数あるが、次の4つの解析手法を解説する。
1. 群無し_経時変化の検証
2. 群有り_全体の経時変化・群間有意差の検証/群ごとの経時変化の検証
3. 時点ごとの群間有意差の検証
4. 時点無し(一列)群間有意差の検証
1.群無し_経時変化の検証
この解析手法が適用できる具体例を示す。
ある降圧剤投与後の血圧の変化に関して、次のようなデータが与えられているとする。
このデータは降圧剤を10mg投与し、投与前、1時間後、3時間後の測定値である。
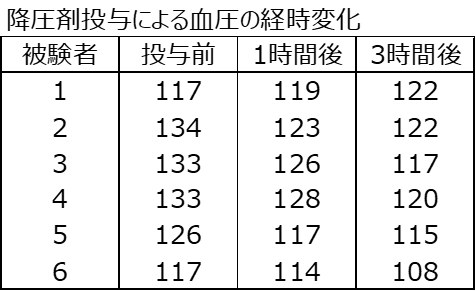
検証結果の平均・標準偏差、平均値折れ線グラフ、分散分析表、多重比較法、効果量を下記に示す。
平均・標準偏差
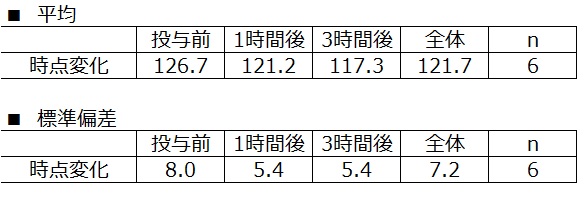
平均値折れ線グラフ
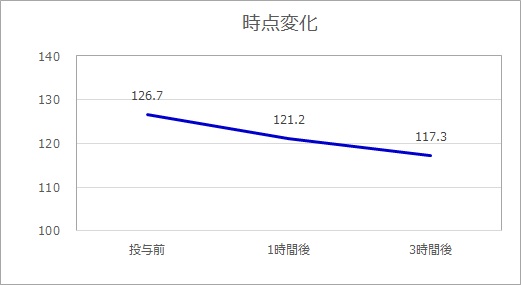
分散分析法
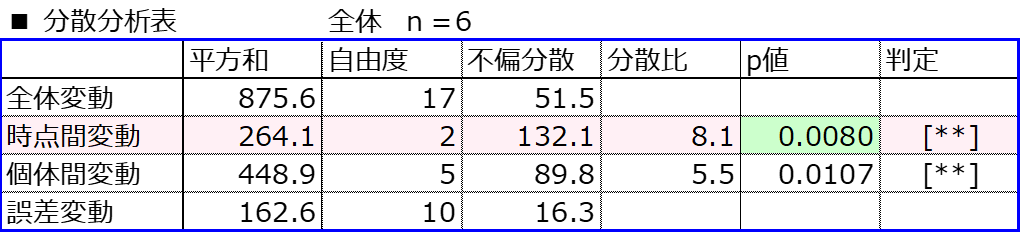
上記の分散分析法は、3つ以上の時点間の平均値の差が統計的に有意かどうかを検定するための統計的方法である。
分散分析法は仮説を立て、分散分析表のp値から仮説の採択有無を判断する。
仮説には帰無仮説と対立仮説がある。
帰無仮説(H0):すべての時点での血圧の母平均は等しい。
各時点の血圧の経時変化は水平である。
対立仮説(H1):少なくとも一つの時点での血圧は他の時点の母平均と異なる。
各時点の血圧の経時変化は水平でない。(増加もしくは減少傾向にある)
分散分析表の時点間変動のp値に着目する。(今回は個体間変動のp値は無視する。)
p値によって、帰無仮説の棄却、対立仮説の採択を判断する。
時点間変動のp値を見ると、p値<0.05なので、帰無仮説を棄却し、対立仮説を採択する。
対立仮説を採択できたので、「各時点の血圧の経時変化は水平でない」が言える。
降圧剤10mg投与によって、各時点の血圧に有意な差があるといえ、降圧剤10mg投与は効果があったといえる。
注.p値>0.05であれば、降圧剤10mg投与は効果があったといえないと判断する。
多重比較法
分散分析法は全体的な平均値の相違を調べる方法であり、どの時点間に有意差があるかは把握できない。
多重比較法は、どこの時点間に有意差があるかを検証する方法である。
多重比較法には二つの方法がある。
① 基準となる時点(対照群)と他時点との比較
ダネット法
② 全時点間相互の比較
チューキー法・ボンフェローニ法
多重比較法は仮説を立て、p値より仮説の採択有無を判断する。
仮説には帰無仮説と対立仮説がある。
帰無仮説(H0):検討する2時点間での血圧の母平均は等しい。
対立仮説(H1):3つのケースがある。
ケース1:検討する2時点間での血圧の母平均は異なる。両側検定という。
ケース2:基準となる時点(対照群)より比較時点の方が大きい片側検定(増加)という。
ケース3:基準となる時点(対照群)より比較時点の方が小さい 片側検定(減少)という。
多重比較法のp値によって、帰無仮説の棄却、対立仮説の採択を判断する。
多重比較法のp値<0.05であれば、帰無仮説を棄却し、対立仮説を採択する。
① 基準となる時点(対照群)と他時点との比較の結果を示す。

片側検定の場合、ダネット検定を適用するのが良い。
投与前に比べ、1時間後、3時間後どちらも有意差があるといえる。
② 全時点間相互の比較の結果を示す。

両側検定の場合、チューキー検定を適用するのが良い。
時点が3個の場合、3×(3-1)÷2=3で3通りの比較結果が出力される。
上記表の結果は、投与前に比べ、3時間後で有意差が見られた。
効果量
効果量は、単に統計的な差があるという情報だけではなく、その差が実際にどれほど実用的な意味を持つのかを示す重要な指標である。研究の結果を評価する際には、統計的有意性と効果量の両方を考慮するのがよい。
効果量はサンプルサイズによって変化することはない。一方で、p値はサンプルサイズを多くすれば、どんどん小さくなっていく性質がある。
したがって、有意差が出たとしても、それは本当に差があるという対立仮説が正しかったからなのか、それともサンプルサイズを無駄に多くして無理やりにp値を小さくし有意差を出したものなのかは分からないので、最近の論文では同時に効果量を記載するように求められることがある。
効果量の算出式は色々あるが、下記の計算式を適用した。
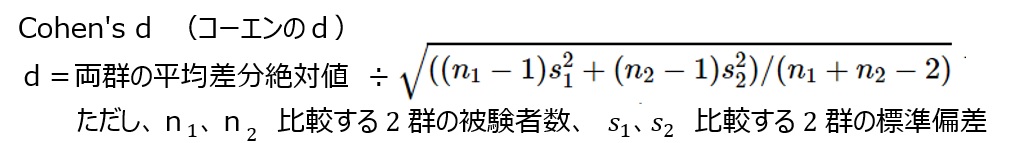
効果量は0から1の間の値で、0.5を超えると、降圧剤投与の効果があると判断できる。
p値の判定について
[ ** ] →p値≦0.01 [ * ] →0.01<p値≦0.05 [ ] →p値>0.05 が付けば有意差があるといえる。
ただし、ボンフェローニ検定は下記で判定する。
k=時点数or群数 m=k×(k-1)/2
[ ** ]→p値≦0.01÷m [ * ]→0.01÷m<p値≦0.05÷m [ ] →p値>0.05÷m
2. 群有り_全体の経時変化・群間有意差の検証/群ごとの経時変化の検証
具体例を示す。
A薬剤の新薬の効果を検証するために、A薬剤の新薬、既存薬、プラセボ(偽薬)を投与した患者に対して、投与直前,30分後,60分後,90分後の4時点における検査を行った。
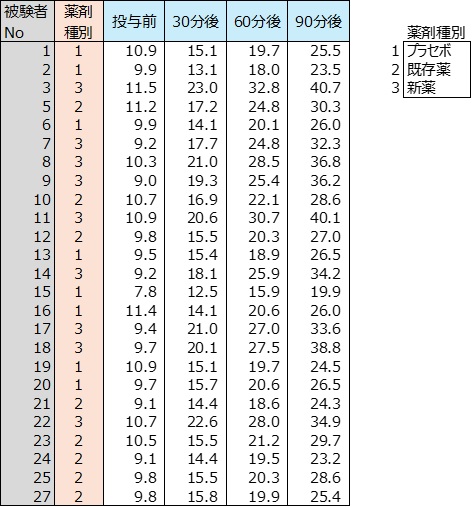
検証結果の群別平均・標準偏差、平均値折れ線グラフ、分散分析法、多重比較法、効果量を下記に示す。
群別平均・標準偏差
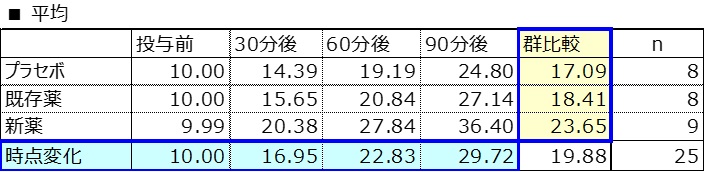
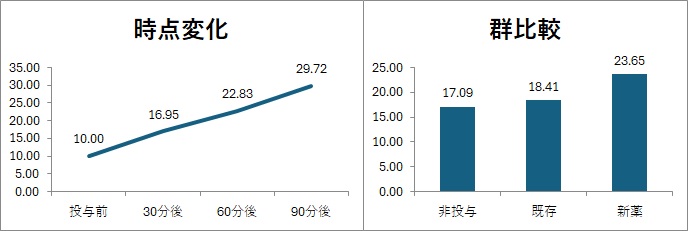
平均値折れ線グラフ
分散分析法
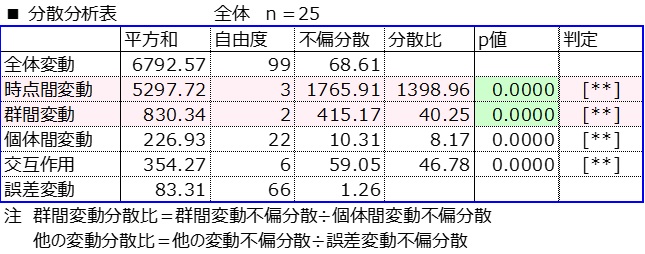
この分散分析は、「群別平均・標準偏差」の平均の時点変化(水色)について調べ、経時変化が統計的に見て有意か、また群比較の平均差(黄色)で群間変動について調べ、母平均値の差が統計的に有意かどうかを検定するための統計的方法である。
① 時点間変動の検証
分散分析表の時点間変動のp値から仮説の採択有無を判断する。
時点間変動の仮説
帰無仮説(H0):すべての時点での測定値の母平均は等しい。
各時点の測定値の経時変化は水平である。
対立仮説(H1):少なくとも一つの時点での測定値は他の時点の測定値と異なる。
測定値の経時変化は水平でない。(増加あるいは減少傾向にある)
時点間変動のp値を見ると、p値<0.05なので、帰無仮説を棄却し、対立仮説を採択する。
対立仮説を採択できたので、「各時点の測定値の経時変化は水平でない」がいえる。
各時点の測定値の傾向に有意な変化があるといえる。A薬剤の投与は新薬、既存薬、プラセボにかかわらず、A薬剤投与は効果があるといえる。
注:p値>0.05であれば、A薬剤投与は効果があるといえないと判断する。
② 群間変動の検証
分散分析表の群変動のp値から仮説の採択有無を判断する。
群間変動の仮説
帰無仮説(H0):すべての群の測定値の母平均は等しい。
対立仮説(H1):少なくとも一つの群の測定値は他の群の測定値と異なる。
群間変動のp値を見ると、p値<0.05なので、帰無仮説を棄却し、対立仮説を採択する。
対立仮説を採択できたので、「少なくとも一つの群の測定値は他の群の測定値と異なる」がいえる。
A薬剤の投与は新薬、既存薬、プラセボで異なるといえる。
注:p値>0.05であれば、A薬剤の投与は新薬、既存薬、プラセボで異なるといえない。
多重比較法
分散分析法は全体的な平均値の相違を調べる方法であり、どの時点間あるいは群間に有意差があるかは把握できない。
多重比較法は、どこの時点間あるいは群間に有意差があるかを検証する方法である。
多重比較法には二つの方法がある。
① 基準となる時点(対照群)と他時点との比較 : ダネット法
② 全時点間相互の比較 :チューキー法、ボンフェローニ法
時点間の多重比較法
多重比較法は仮説を立て、p値より仮説の採択有無を判断する。
仮説には帰無仮説と対立仮説がある。
帰無仮説(H0):検討する2時点間での測定値の母平均は等しい。
対立仮説(H1):3つのケースがある。
ケース1:検討する2時点間での測定値の母平均は異なる 両側検定という。
ケース2:基準となる時点(対照群)より比較時点の方が大きい片側検定(増加)という。
ケース3:基準となる時点(対照群)より比較時点の方が小さい片側検定(減少)という。
多重比較法のp値によって、帰無仮説の棄却、対立仮説の採択を判断する。
多重比較法のp値<0.05であれば、帰無仮説を棄却し、対立仮説を採択する。

片側検定の場合、ダネット検定を適用するのが良い。
投与前に比べ、30分後、60分後、90分後いずれも有意差があるといえる。
注.:両側検定を選んだ場合、チューキー検定を適用するのが良い。
群間の多重比較法
多重比較法は仮説を立て、p値より仮説の採択有無を判断する。
仮説には帰無仮説と対立仮説がある。
帰無仮説(H0):検討する2群間での測定値の母平均は等しい。
対立仮説(H1):検討する2群間での測定値の母平均は異なる。
両側検定という。 注:片側検定はない、
多重比較法のp値によって、帰無仮説の棄却、対立仮説の採択を判断する。
多重比較法のp値<0.05であれば、帰無仮説を棄却し、対立仮説を採択する。

群間比較の場合ダネット検定はない。両側検定のみである。
チューキーp値<0.05より、新薬はプラセボ及び既存薬に比べ有意差が認められ、新薬投与の効果はあったといえる。
群ごとの経時変化の検証の平均折れ線グラフ、群別の検定結果を示す。
平均値折れ線グラフ
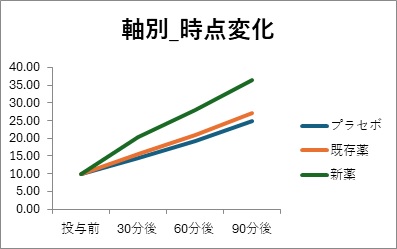
群1:プラセボ
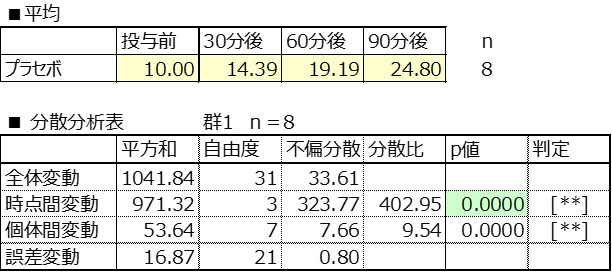

群2:既存薬
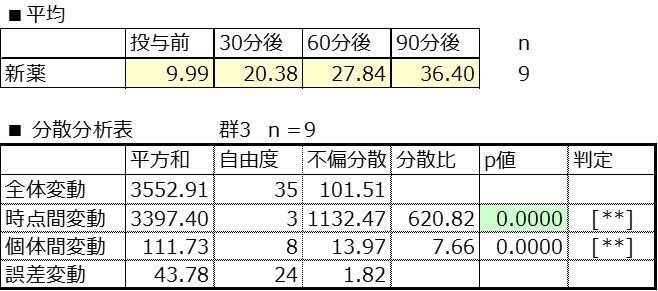

群3:新薬
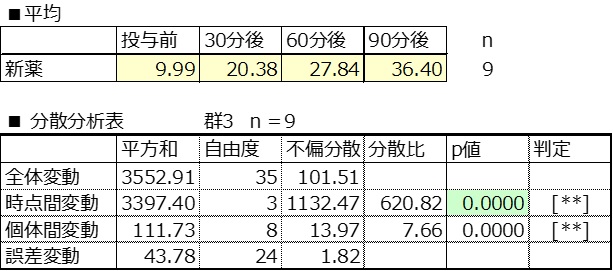

新薬に着目する。
時点間変動p値<0.05より、新薬投与の測定値の経時変化は有意な傾向を示している。
多重比較p値より、投与前に比べ、30分後、60分後、90分後の想定値は高まり、いずれも有意差があるといえる。

