3 .時点ごとの群間有意差の検証
この解析手法が適用できる具体例を示す。
A薬剤の新薬の効果を検証するために、A薬剤の新薬、既存薬、プラセボ(偽薬)を投与した患者に対して、投与直前,30分後,60分後,90分後の4時点における検査を行った。
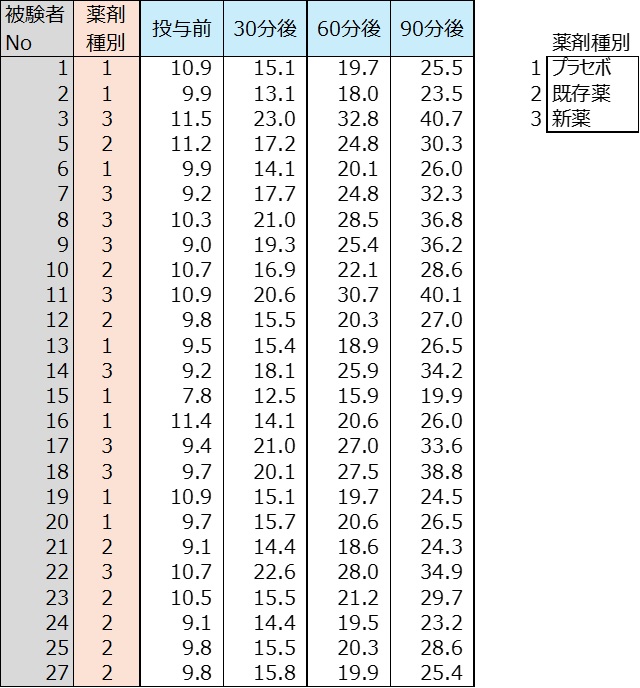
多重比較要約 チューキー(両側)と時点ごとの4つの平均値棒グラフ・差分折れ線グラフ、分散分析法、多重比較法、効果量を下記に示す。
多重比較要約 チューキー(両側)

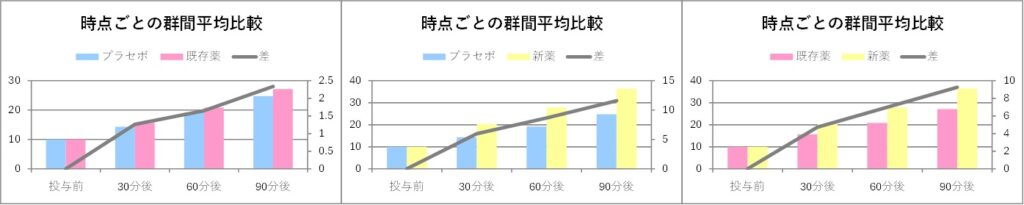
平均値棒グラフ・差分折れ線グラフ
投与前
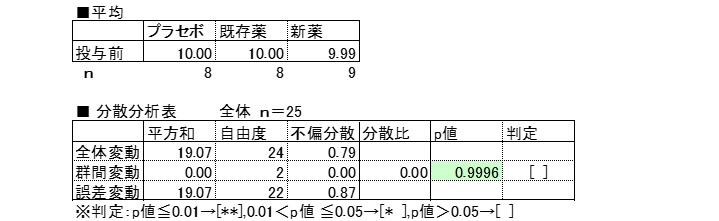

分散分析表の群間変動のp値から仮説の採択有無を判断する。
群間変動の仮説
帰無仮説(H0):投与前はすべての群の測定値の母平均は等しい。
対立仮説(H1):投与前は少なくとも一つの群の測定値は他の群の測定値と異なる。
群間変動のp値を見ると、p値>0.05なので、帰無仮説を棄却できないため、対立仮説を採択できない。
投与前の群間平均は有意な差があるとはいえない。
30分後
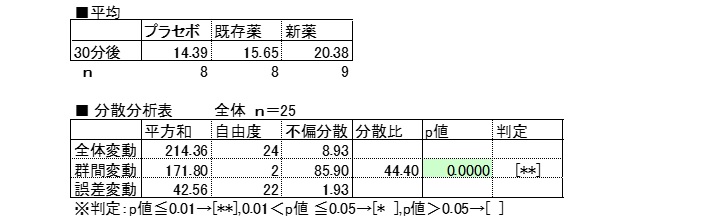

分散分析表の群間変動のp値から仮説の採択有無を判断する。
群間変動の仮説
帰無仮説(H0):投与30分後はすべての群の測定値の母平均は等しい。
対立仮説(H1):投与30分後は少なくとも一つの群の測定値は他の群の測定値と異なる。
分散分析表の群間変動p値<0.05より、帰無仮説を棄却し、対立仮説を採択する。
投与30分後の群間平均は有意な差があるとはいえる。
では、どの群とどの群で有意な差があるか群間の多重比較法を確認する。
多重比較法は仮説を立て、p値より仮説の採択有無を判断する。
仮説には帰無仮説と対立仮説がある。
帰無仮説(H0):検討する2群間での測定値の母平均は等しい。
対立仮説(H1):検討する2群間での測定値の母平均は異なる。
両側検定という。 注:片側検定はない、
多重比較法のp値によって、帰無仮説の棄却、対立仮説の採択を判断する。
多重比較法のp値<0.05であれば、帰無仮説を棄却し、対立仮説を採択する。
多重比較検定チューキーp値<0.05より、新薬はプラセボ及び既存薬に比べ有意差が認められ、新薬投与の効果はあったといえる。
60分後
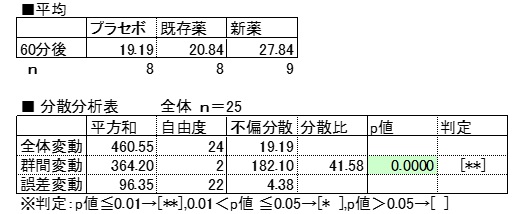

分散分析表の群間変動p値<0.05より、投与60分後の群間平均は有意な差があるとはいえる。
多重比較検定チューキーp値<0.05より、新薬はプラセボ及び既存薬に比べ有意差が認められ、新薬投与の効果はあったといえる。
90分後
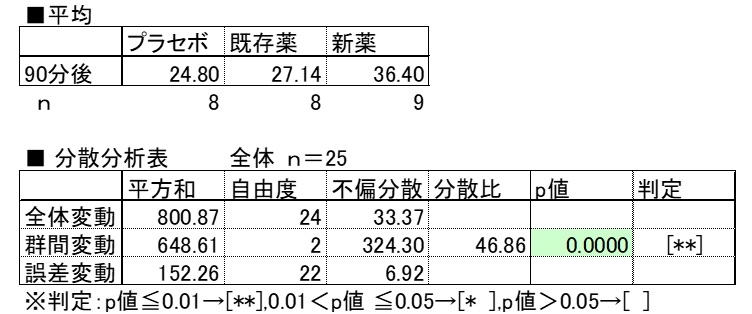

分散分析表の群間変動p値<0.05より、投与90分後の群間平均は有意な差があるとはいえる。
多重比較検定チューキーp値<0.05より、新薬はプラセボ及び既存薬に比べ有意差が認められ、新薬投与の効果はあったといえる。
4. 時点無し(一列)群間有意差の検証
この解析手法が適用できる具体例を示す。
ほほ同じレベルの生徒を対象にトレーニング方法を色々変えて一ヵ月間訓練した。訓練終了後てテストをしたときの得点である。どのトレーニング方法が良かったかをトレーニング無しとの比較において明らかにしたい。
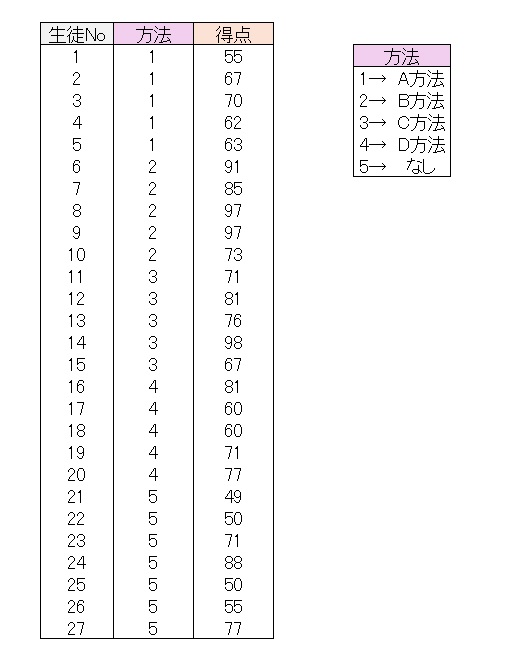
検証結果の群平均・標準偏差、平均値棒グラフ、分散分析法、多重比較法、効果量を下記に示す。
群平均・標準偏差
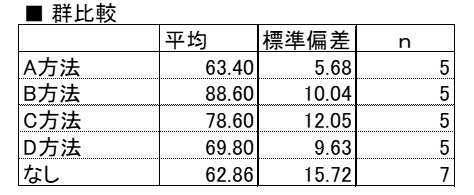
平均値棒グラフ
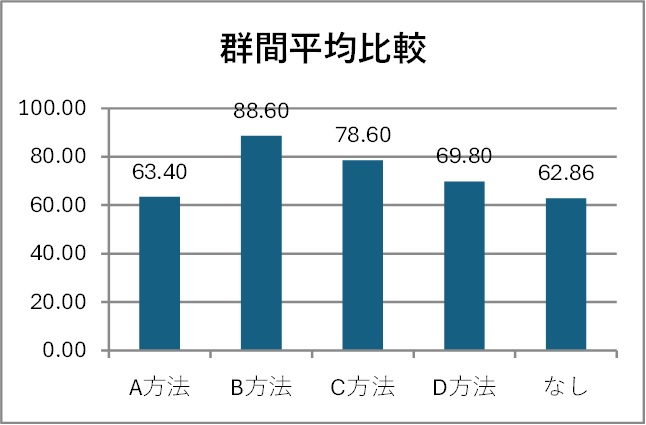
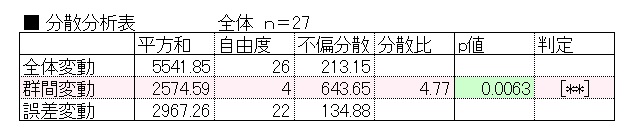
分散分析法
多重比較・効果量

散分析表の群間変動のp値から仮説の採択有無を判断する。
群間変動の仮説
帰無仮説(H0):すべての群の測定値の母平均は等しい。
対立仮説(H1):少なくとも一つの群の測定値は他の群の測定値と異なる。
分散分析表の群間変動p値<0.05より、帰無仮説を棄却し、対立仮説を採択する。
群間平均は有意な差があるとはいえる。
分散分析表の群間変動p値<0.05より、トレーニング方法の効果はあるとはいえる。
では、どのトレーニング方法で有意な差があるか群間の多重比較法を確認する。
多重比較法は仮説を立て、p値より仮説の採択有無を判断する。
仮説には帰無仮説と対立仮説がある。
帰無仮説(H0):検討する2群間での測定値の母平均は等しい。
対立仮説(H1):3つのケースがある。
ケース1:検討する2時点間での測定値の母平均は異なる 両側検定という。
ケース2:基準となる時点(対照群)より比較時点の方が大きい片側検定(増加)という。
ケース3:基準となる時点(対照群)より比較時点の方が小さい片側検定(減少)という。
今回はケース2の対立仮説を立てる。
多重比較法のp値によって、帰無仮説の棄却、対立仮説の採択を判断する。
多重比較法のp値<0.05であれば、帰無仮説を棄却し、対立仮説を採択する。
多重比較検定ダネットp値<0.05より、B方法のトレーニングの効果はあったといえる。

