共分散分析(ANCOVA) ≪ 1/4 ≫
はじめに
分散分析はAnalysis of varianceを略してANOVA(アノバ)という。
共分散分析はAnalysis of covarianceを略してANCOVA(アンコバ)という。
共分散分析は分散分析と同じように母平均の差の検定(群間比較)を行う解析手法で、帰無仮説、対立仮説は次となる。
帰無仮説 H0:群間の主効果が同じ(母平均に差がない)
対立仮説 H1:群間の主効果に差がある(母平均に差がある)
共分散分析が分散分析と異なる点は共変量の影響を取り除いて母平均の差の検定を行うことである。
分散分析についてのおさらい
共分散分析を解説する前に分散分析についておさらいをする。
分散分析には3つの解析手法がある。
・一元配置分散分析(別名:一元配置法)
・二元配置分散分析(別名:二元配置法)
・多元配置分散分析(別名:多元配置法)
共分散分析は一元配置分散分析に類似した解析手法なので、ここでは一元配置分散分析についておさらいをする。
一元配置分散分析で適用できるデータ例を示す。
1列目に個体名、2列目に群、3列目に数量項目のデータ表がある。(A表)
A表を編集して、B表を作成する。
B表は、1列目を群1(20代)、2列目を群2(30代)、3列目を群3(40代)の数量データとする。
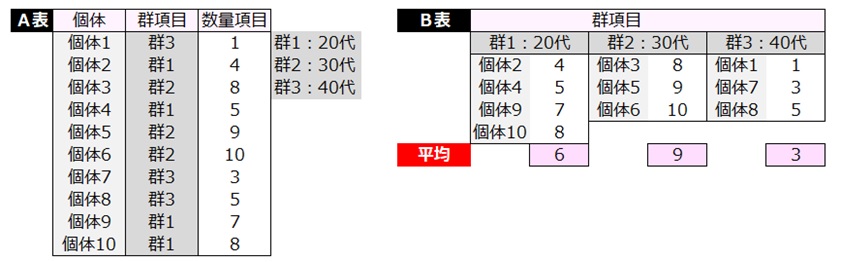
一元配置分散分析はB表の各群の平均値を検討する手法である。
データには「対応のないデータ」と「対応のあるデータ」がある。
<対応のないデータ>
20代、30代、40代など同一人物でない者同士を比較する場合
<対応のあるデータ>
前日、1日後、2日後など同一人物で経過を追って比較する場合
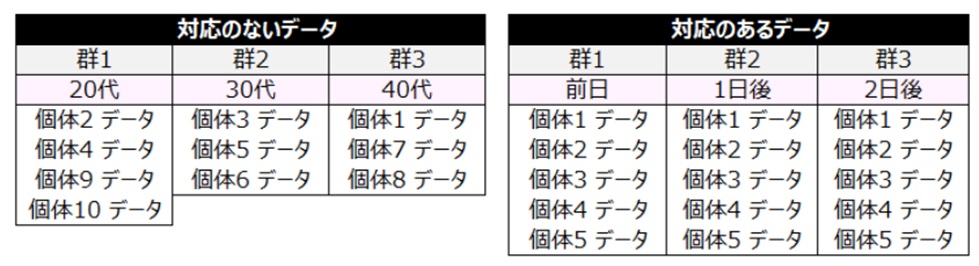
留意点1 対応のあるデータにおいて群が時間的経過を示す場合、対応のあるデータの分散分析を
経時データ分散分析という。
留意点2 共分散分析は対応のないデータについて解析するものである。
留意点3 以降に示す分散分析の名称は対応のないデータの一元配置分散分析のことである。
分散分析は全体的な平均値の相違を調べる方法で、どの群間に有意差があるかまでは把握できない。
分散分析によって全体的な相違が認められた場合、どこの群間に有意差があるかは検定手法によって検証する。
群数が3群以上の場合の検定手法は多重比較検定(ボンフェローニ、チューキー、ホルム、ダネット等)、群数が2群の場合はt検定である。
分散分析は3群以上のデータについて解析する手法と言われているが2群データについても分散分析は行える。2群データの分散分析を行った場合、分散分析のp値はt検定のp値と同じになる。ゆえに、2群データについては分散分析を行う必要がない。
B表の20代と30代のデータで分散分析とt検定を行った。両者のp値が一致していることを確認されたい。
留意点:サンプルサイズは小さいが母平均は正規分布であるとしてU検定でなくt検定を適用

次に解説する共分散分析は、共変量の影響を取り除いて群間相互の母平均の差を調べることを目的としているので、3群以上のデータはもちろんのこと、2群データでも分析が行える。
留意点:共分散分析における共変量調整済みの群間相互の母平均の差の検定は2群も3群以上も重回帰分析の標準誤差を適用したt検定で行う。
2群データの共分散分析を解説
具体例
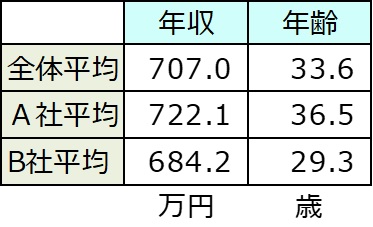
ここで具体例を示す。A社とB社を取り上げて、20歳から39歳の社員の平均年収はどちらが高いかを調べることにした。A社から15人、B社から10人をランダムに選び年収調査を行った。
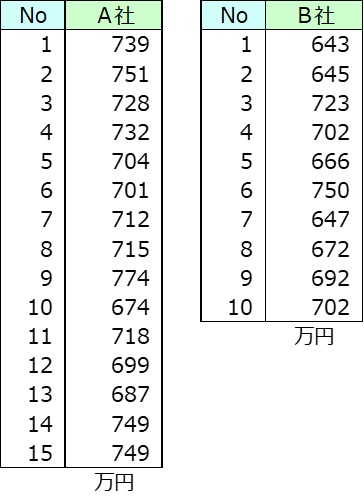
年収の平均を調べた。
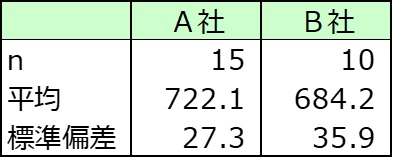
A社は722万円、B社は684万円でA社がB社を上回った。
会社全体(母集団)についても違いがあるかをt検定で調べた。
p値=0.0146<0.05より、20歳から39歳社員の年収はA社の方がB社より高いといえる。
注.サンプルサイズは小さいが母集団における年収は正規分布に従っていることが分かっているものとしてノンパラメトリック検定のU検定でなくt検定を適用した。
この結果をみて入社するとした場合、「業務内容が同じとしてどちらの会社を選択するか」と問われれば、平均年収の高いA社を選ぶ人が多いであろう。
だが観察力の鋭い人はもうちょっと詳細な情報がないとA社に行きたいかは分からないと答えるであろう。この人が思う情報には色々あると思うがその内の一つに社員の年齢がある。
A社はB社に比べ年齢の高い人が多くおり、年齢に引っ張られて平均年収が高くなっているからである。
一般的に年齢が高くなれば、年収も上がっていく傾向がある。
つまり、平均年収が高い要因として、2つの可能性がある。
① 本当にその会社の平均年収が高い
② その会社の従業員の年齢が高いためその会社の平均給与が高い
A社の平均年収が高い要因が、①の「本当にその会社の平均年収が高い」であれば、A社に行く。
しかし、A社の平均年収が高い要因が、②の「その会社の従業員の年齢が高いためその会社の平均年収が高い」であれば、A社に入社する選択は別の要因を検討してから決める。
つまり言い換えると下記のようになる。
A社とB社の平均年収の差は、本当にA社とB社の会社の違い(給与水準の違い)によるものなのか、その会社の従業員の年齢の違い(年齢という交絡因子の違い)によるものなのかを明らかにしないと、真実がわからない。
なので、「本当にA社とB社の給与水準の違い」なのか「年齢という交絡因子」によるものなのかを解析してみようということになる。
この問題を解決してくれるのが共分散分析である。
共分散分析は「年収に影響を与えていると考えられる年齢の影響を除いたA社とB社の比較ができる」解析手法である。
共分散分析では交絡因子を共変量という。
共分散分析は、説明変数の中に、共変量(平均値に影響を与える変数、この例では年齢)があった場合には、その共変量の影響を取り除いて、「群間比較」(平均値の比較)を行うことができる解析手法である。
<2群データ>共分散分析のデータ
共分散分析のデータ共分散分析に用いる解析データは次の3つである。
① 【群データ】 カテゴリーデータ:この例ではA会社、B会社
② 【目的変数】 数量データ:この例では年収
③ 【共変量】 数量データ:この例では年齢
先に示したデータに年齢を加えたデータを示す。
群数2の共分散データ
<2群データ>目的変数と共変量との相関関係及び回帰式
共分散分析を行う前に、共変量と目的変数との相関関係を調べておく必要がある。
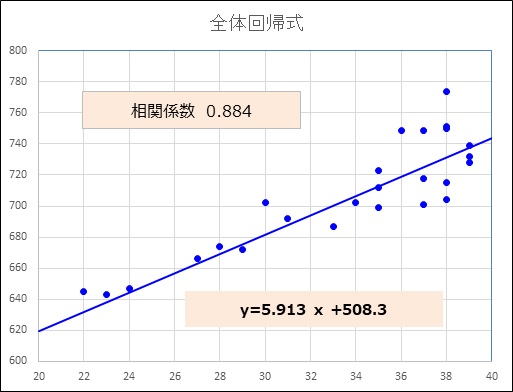
この例では年齢と年収の相関係数を調べると0.884である。
相関係数が高い値を示したので年収は年齢の影響を受けているといえる。そこで年齢の影響を除去してA社とB社の平均年収を比較することになる。
仮に年齢と年収の相関が低ければ、年齢の影響を除去することなくA社とB社の平均年収を比較することになる。
言い換えれば共分散分析をすることなく、分散分析でA社とB社の平均年収に違いがあるかを調べればよいということである。
共分散分析をする前に行うこと
① 縦軸に目的変数(年収)、横軸に共変量(年齢)を取り散布図を作成する。
② 相関係数を算出する。
③ 目的変数と共変量は無相関であるかを検定する。
④ 散布図に回帰直線を当てはめる。
⑤ 回帰式の係数は0であるかを検定する。
③と⑤は同じことなのでどちらかをする。
① 散布図、②相関係数、④全体回帰式の結果を示す。
⑤の回帰式の係数は0であるかの検定結果を示す。 ③の結果は?

p値<0.05より、「回帰係数は0ではない」といえるので、共分散分析を行える。
回帰式の係数は0(無相関)の判定が示された場合、共分散分析は行わない。
母平均の差はt検定のみをすればよい。
<2群データ>調整済み平均
共分散分析では年齢(共変量)の影響を除去した年収(目的変数)の平均を算出することを目的としている。
この平均を調整済み平均という。
群別に調整済み平均を算出し、A社とB社で調整済み平均に有意差があるかを検証する。
この例の調整前平均及び調整済み平均の有意差検定の結果を示す。

年収平均を見ると、A社722.1万円、B社684.2万円で差は37.9万円である。
共変量の影響を取り除いた調整平均をみると、A社703.7万円、B社711.8万円でその差は-8.1万円と差は小さくなった。
p値=0.4015>0.05でA社とB社の平均年収は差がないといえる。
注. 調整済み平均の求め方、有意差検定の計算方法は次節で解説する。

