共分散分析(ANCOVA) ≪ 2/4 ≫
<2群データ>調整済み平均の算出の考え方
調整済み平均の求め方を解説する。
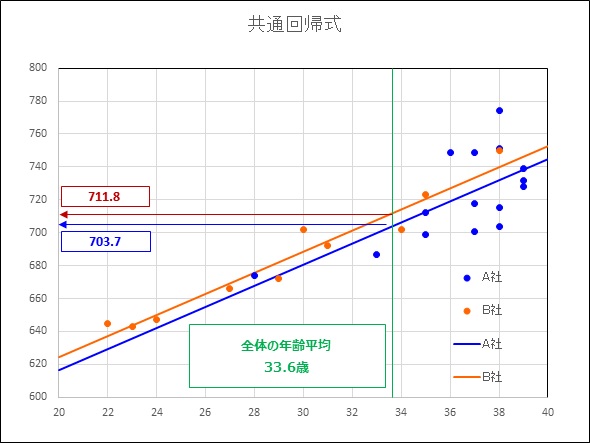
下記図は、縦軸を年収(目的変数)、横軸を年齢(共変量)とした散布図である。
A社(青色)の散布点に回帰直線を引く。(青線)
B社(茶色)の散布点に回帰直線を引く。(茶線)
年齢の全体平均33.6歳の縦線を引く。(緑線)
緑線と青線の交点から横線を引き縦軸の交点を求める。
緑線と茶線の交点から横線を引き縦軸の交点を求める。
縦軸との交点が調整済み平均である。
調整済み平均は、B社711.8万円、A社703.7万円である。
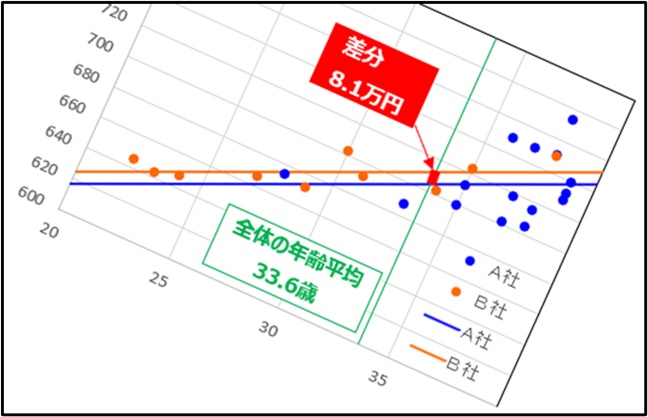
下図は、上図を回帰直線が水平になるまで回転したものである。
水平にした2本の比較は年齢の影響を除去した年収の比較となる。
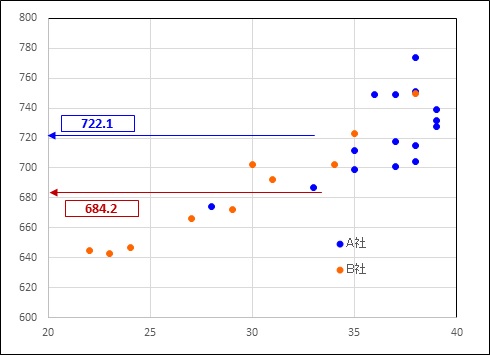
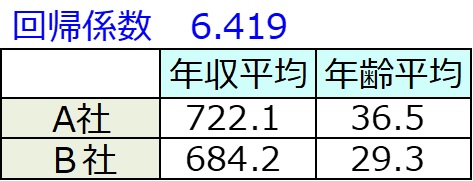
下図は元データのA社とB社の年収平均を示したものである。
A社の年収平均は722.1万円でB社の684.2万円を上回っている。
調整済み平均はA社がB社を下回っている。両者の平均の違いを確認されたい。
【結論】
A社とB社の平均年収を比較するとA社は722.1万円でB社の684.2万円を37.9万円上回っているが、年齢の影響を除去して比較するとA社703.7万円、B社711.8万円でA社とB社の差は-8.1万円である。
年齢の影響を除去するとA社とB社の平均年収差は小さくなった。
<2群データ>個別回帰式
「調整済み平均の算出の考え方」での図は、回帰直線を当てはめたと述べたが、正しくは共通回帰式というものを適用したものである。我々が通常用いる回帰式とは別物である。通常の回帰式を共通回帰式と識別するために 個別回帰式と呼ぶことにする。
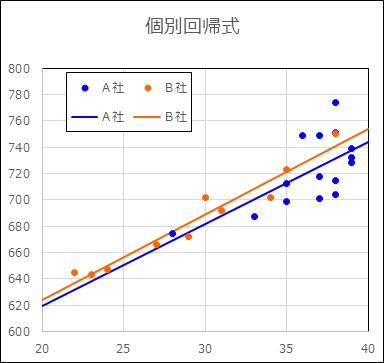
個別回帰式を示す。
A社 y=6.235x+494.8
B社 y=6.503x+493.7
直線の傾きはA社がB社をやや下回るがどちらも右肩上がりの傾向を持つ、傾向がほぼ同じ傾きといってよさそうである。
下記の1、2のように個別回帰式の2本の直線の傾きが異なると、共変量(年齢)の影響を正確に除去できない。理想は3のように傾きが同じ(平行)になっていることである。
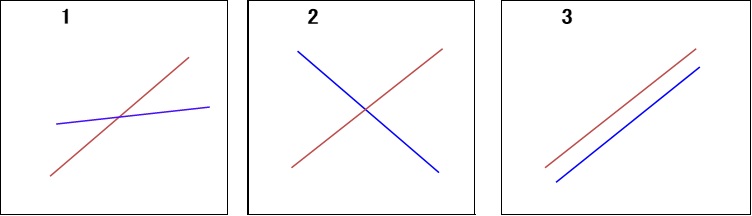
そこで、共分散分析を行う前に2本の直線の傾きが同じ(平行)であるかの検定をしておく必要がある。

帰無仮説H0:2本の直線は平行である
対立仮説H1:2本の直線は平行でない
p値<0.05 → 「2本の直線は平行である」を棄却 → 平行であるといえない
p値≧0.05 → 「2本の直線は平行である」を棄却できない → 平行である
上記はp値>0.05より、2本の直線は「平行である」といえ、共分散分析は行える。
<2群データ>共通回帰式
母集団における個別回帰式の2本の直線は平行といえるので、散布点に最もあてははまりのよい平行である回帰式を当てはめる。これが共通回帰式である。
共通回帰式はA社とB社の2つであるが、2つの回帰式の係数は同じ値、定数項は異なる。
共通回帰式の係数の求め方
・偏差データを算出する。
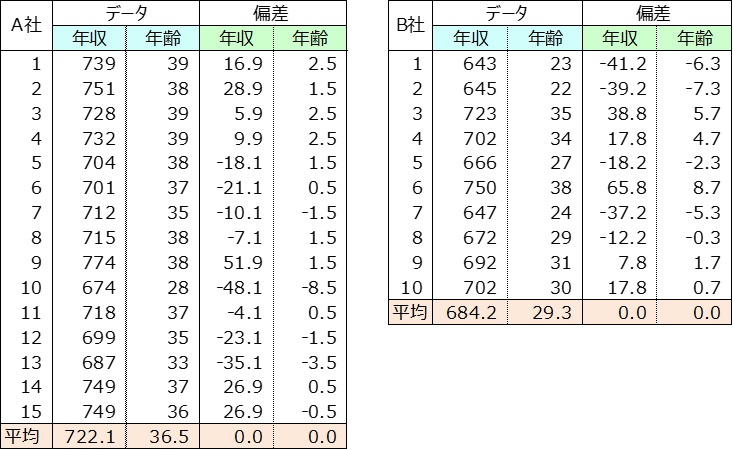
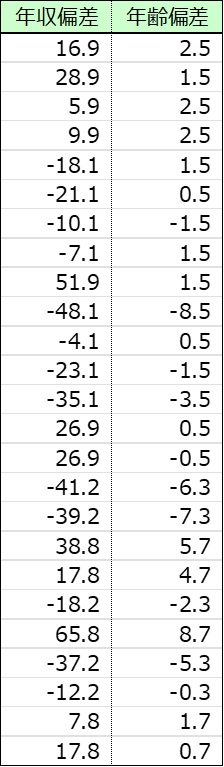
・A社偏差データ15人とB社偏差データ10人を縦に並べ、25人の偏差データを作成する。
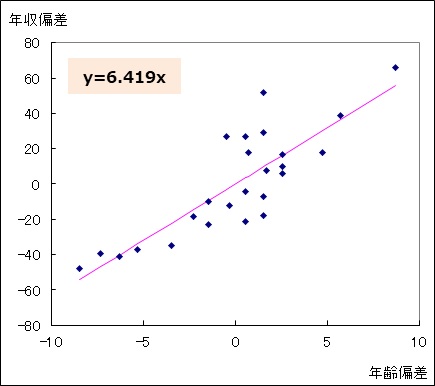
・25人の偏差データの散布図と全体回帰式を求める。全体回帰式はy=6.419xである。
・共通回帰式A社の回帰係数は全体回帰式の係数6.419とする。
・共通回帰式B社の回帰係数は全体回帰式の係数6.419とする。
共通回帰式の定数項の求め方
定数項は次によって算出する。
定数項は次によって算出する。
A社定数項=年収平均-回帰係数×年齢平均=722.1-6.419×36.5=488.0
B社定数項=年収平均-回帰係数×年齢平均=684.2-6.419×29.3=496.1
求められた共通回帰式
A社 y=6.419x+488.0
B社 y=6.419x+496.1
<2群データ>調整済み平均の算出式
共通回帰式に全体の年齢平均を代入する。
調整済み平均=共通回帰式の回帰係数×共変量(年齢)の全体平均+定数項
A社調整済み平均=6.419×33.6+488.0=703.7
B社調整済み平均=6.419×33.6+496.1=711.8
<2群データ>別の事例
ここまでの事例は、2社の平均差は大きいが調整済み平均の差は小さいというものである。
下記の事例は、2社の平均差は小さいが調整済み平均の差は大きいというものである。
データ
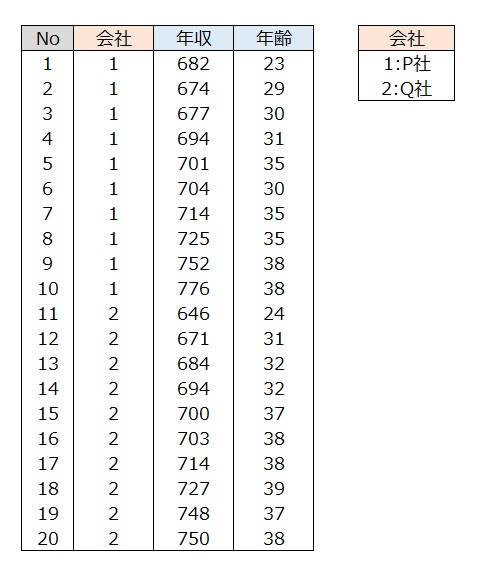
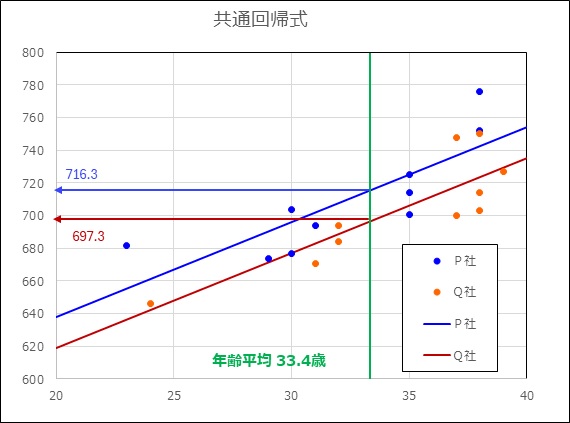

年収平均を見ると、P社709.9万円、Q社703.7万円で差は6.2万円である。
共変量の影響を取り除いた調整平均をみると、P社716.3万円、Q社697.3万円でその差は19万円と差は大きくなった。p値=0.0.429<0.05でP社とQ社の平均年収は差があるといえる。(P社はQ社より平均年収は高いといえる)

