共分散分析(ANCOVA) ≪ 3/4 ≫
3群データの共分散分析を解説
3群データで調整平均、母平均の差の検定の計算方法を示す。
1 データ
2 平均
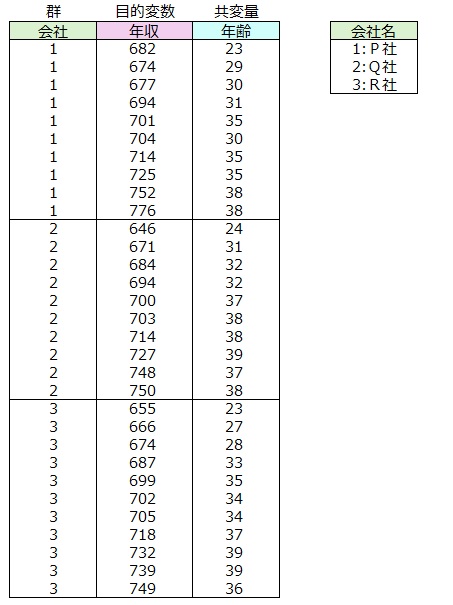
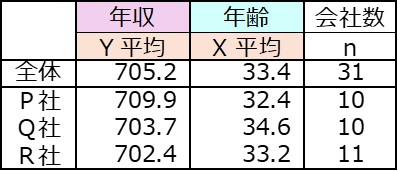
<3群データ>共分散分析の手順
①_1 全データにおける目的変数(年収)と共変量(年齢)の散布図を作成
①_2 全データにおける目的変数(年収)と共変量(年齢)の相関係数を算出
①_3 全データにおける目的変数(年収)と共変量(年齢)の全体回帰式を算出
② 目的変数と共変量の関係性を調べ、共分散分析をすべきかを把握
→ 回帰係数0の検定(回帰係数有意性検定)
③ 3個の個別回帰式を算出
④ 個別回帰式3つの直線が平行であるかを調べ、共分散分析をすべきかを把握
→ 平行性の検定
⑤ 3個の共通回帰式を算出
⑥ 共通回帰式に全データ年齢平均を代入し、共変量調整済み平均を算出
⑦ 調整済み平均の有意差検定
<3群データ>全体回帰式
1 全データにおける目的変数(年収)と共変量(年齢)の散布図を作成
2 全データにおける目的変数(年収)と共変量(年齢)の相関係数を算出
年収と年齢の相関係数は0.825である
3 全データにおける目的変数(年収)と共変量(年齢)の全体回帰式を算出
全体回帰式は y=5.37X+526.1である。
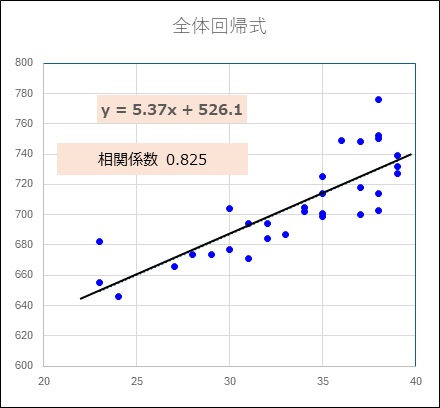
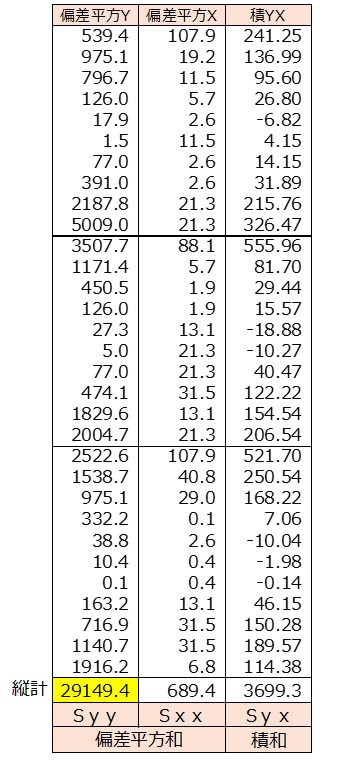
相関係数、全体回帰式の求め方を示す。
偏差平方 y=(個別yデータ-y平均)2
例 No1 (682-705.2)2 =539.4
偏差平方 x=(個別xデータ-x平均)2
例 No1 (23-33.4)2 = 107.9
積 yx=(個別yデータ-y平均)× (個別xデータ-x平均)
=(682-705.2) ×(23-33.4)=241.25
偏差平方和 Syy=29149.4
偏差平方和 Sxx=689.4
積和 Syx=3699.3
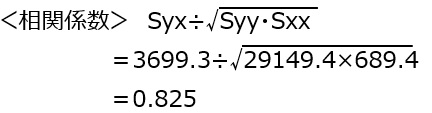
Excel関数 =CORREL(yデータ列,xデータ列)
Enter 0.825
<傾き> Syx ÷Sxx
=3699.3÷689.4=5.37
Excel関数 =SLOPE(yデータ列,xデータ列)
Enter5.37
<切片(定数項)> y平均-傾き× X平均
=705.2-5.37×33.4=526.1
Excel関数 =INTERCEPT(yデータ列,xデータ列)
Enter526.1
注. 以降、切片と定数項の用語が使われるが同じ意味である。
<3群データ>回帰係数0の検定(回帰係数有意性検定)
共分散分析を行う前に、共変量と目的変数との相関関係を調べておく必要がある。
両者、この例では年齢との年収の相関係数を調べると0.825である。
相関係数が高い値を示したので年収は年齢の影響を受けているといえる。
そこで年齢の影響を除去してP社とQ社とR社の平均年収を比較することになる。
仮に年齢と年収の相関が低ければ、年齢の影響を除去することなく会社相互の平均年収を比較することになる。
言い換えれば共分散分析をすることなく、分散分析で3社間の平均年収に違いがあるかを調べればよいということである。
そこで母集団における、年齢と相関は0でない相関があるか(回帰係数は0でないか)を検定することになる。
検定結果を示す。

p値<0.05より、有意水準0.05で「回帰係数は0ではない」といえる。
年収は年齢の影響を受けているので、調整済み平均で3社間を比較しなければならない。
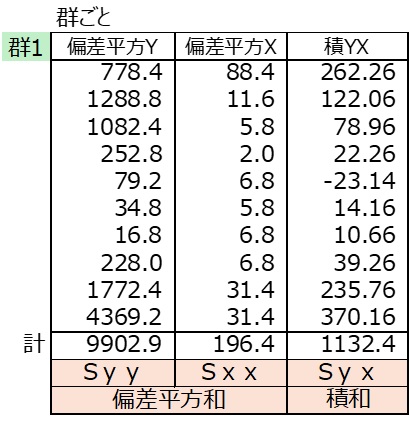
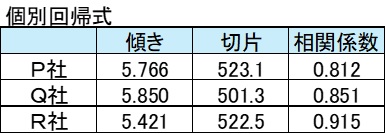
<3群データ>個別回帰式
全回帰式で行ったことを群ごとに行う。
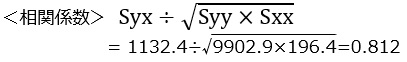
Excel関数 =correl(yデータ列,xデータ列)
Enter0.812
<傾き> Syx/Sxx
=1132.4÷196.4=5.766
Excel関数 =slope(yデータ列,xデータ列)
Enter 5.766
<定数項> Y平均-傾き×X平均
=709.9-5.766×32.4=523.1
Excel関数 =intercept(yデータ列,xデータ列)
Enter523.1
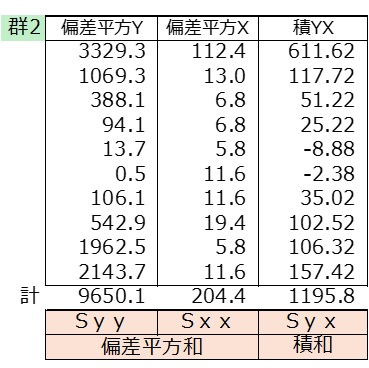
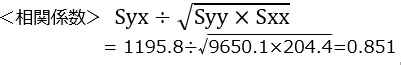
Excel関数 =correl(yデータ列,xデータ列)
Enter0.8
<傾き> Syx÷Sxx
1195.8÷204.4=5.850
Excel関数 =slope(yデータ列,xデータ列)
Enter 5.850
<定数項> Y平均-傾き×X平均
=703.7-5.850×34.6=501.3
Excel関数 =intercept(yデータ列,xデータ列)
Enter501.3
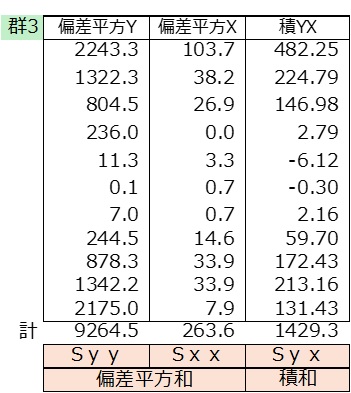
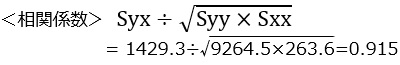
Excel関数 =correl(yデータ列,xデータ列)
Enter 0.915
<傾き> Syx÷Sxx
1429.3÷263.6=5.421
Excel関数 =slope(yデータ列,xデータ列)
Enter5.421
<定数項> Y平均-傾き×X平均
=702.4-5.766×33.2=522.5
Excel関数 =intercept(yデータ列,xデータ列)
Enter 522.5
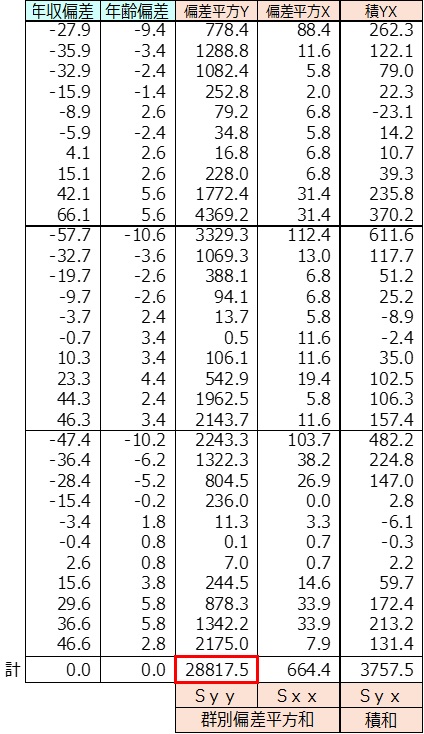
※1 個別回帰式_群合算 Syy 偏差平方和 =9902.9 + 9650.1 + 9264.5 = 28817.5
下記の個別回帰式の直線を描いた散布図を作成した。
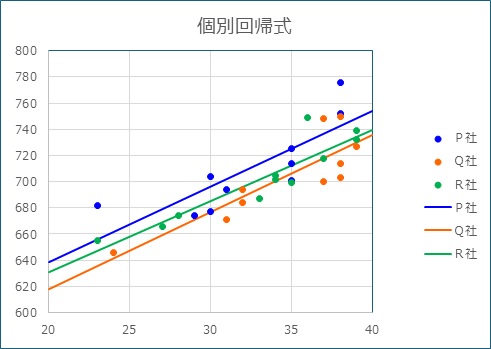
<3群データ>平行性の検定
上記に示した個別回帰式の3本の直線の傾きが同じとみなされた時、共通回帰式の当てはめを行える。
そこで、「個別回帰式の3本の直線の傾きが同じ」→「回帰係数が平行である」かを調べる検定を行う必要がある。
この検定を回帰係数平行性の検定という。
検定結果を示す。

帰無仮説H0:3本の直線は平行である
対立仮説H1:3本の直線は平行でない
p値>0.05より、対立仮説を採択できない。「平行でない」が言えない。
ゆえに拡大解釈をして「回帰係数は平行である」といえる。
3本の回帰係数が平行であると言えたので調整済み平均を算出することができる。
注. 回帰係数平行性の検定の計算方法は「回帰係数有意性検定を解説」にて解説する。
<3群データ>共通回帰式
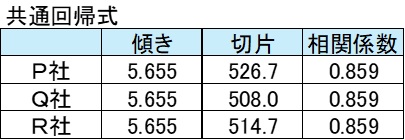
共通回帰式はP社、Q社、R社ごとに3個求める。
ただし、3個の共通回帰式の回帰係数は同じで定数項は異なる。
共通の回帰係数は、下記の25人の年収偏差、年齢偏差を作成し、これらデータから求めた回帰係数とする。
共通回帰式の計算方法を示す。
年収偏差=年収データ-群別年収平均
共通回帰式の計算方法を示す。
年収偏差=年収データ-群別年収平均
例 No1の場合 データ682-年収群1平均709.9=-27.9
年齢偏差=年齢データ-群別年齢平均
例 No11の場合 データ24-年齢群2平均34.6=-10.6
<傾き> Syx÷Sxx
=3757.5÷664.4=5.655
Excel関数 =slope(年収偏差データ、年齢偏差データ)
Enter5.655
P社 定数項=年収平均-回帰係数×P社年齢平均=709.9-5.655×32.4=526.7
Q社 定数項=年収平均-回帰係数×Q社年齢平均=703.7-5.655×34.6=508.0
R社 定数項=年収平均-回帰係数×R社年齢平均=702.4-5.655×33.2=514.7
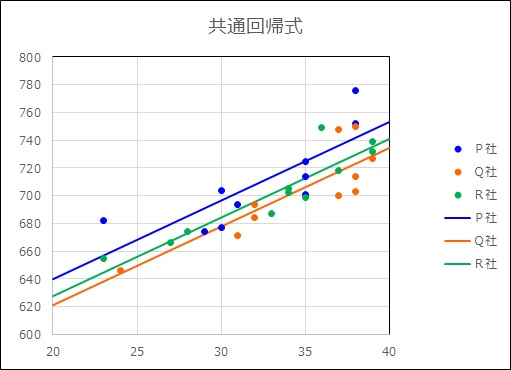
3個の共通回帰式の結果とグラフを示す。
<3群データ>調整済み平均
調整済み平均の求め方を解説する。
調整済み平均は、共通回帰式に年齢の全体平均を代入することによって求められる。
《群1》 P社の共通回帰式 y=5.655x+526.7
《群2》 Q社の共通回帰式 y=5.655x+508.0
《群3》 R社の共通回帰式 y=5.655x+514.7
年齢の全体平均は33.4歳である。
《群1》 P社の調整済み平均 5.655×33.4+526.7=715.5
《群2》 Q社の調整済み平均 5.655×33.4+508.0=696.8
《群3》 R社の調整済み平均 5.655×33.4+514.7=703.5
<3群データ>調整済み平均の有意差検定
調整済み平均の有意差検定の結果を示す。

P社とQ社の年収平均を見ると、P社709.9万円、Q社703.7万円で差は6.2万円である。
共変量の影響を取り除いた調整済み平均をみると、P社715.5万円、Q社696.8万円でその差は18.7万円と差は大きくなった。p値=0.0213<0.05でP社とQ社の平均年収は差があるといえる。(P社はQ社より平均年収は高いといえる)
P社とR社の年収平均を見ると、P社709.9万円、R社702.4万円で差は7.5万円である。
共変量の影響を取り除いた調整済み平均をみると、P社715.5万円、R社703.5万円でその差は12.0万円と差は大きくなった。p値=0.1146>0.05でP社とR社の平均年収は差があるといえない。
Q社とR社の年収平均を見ると、Q社703.7万円、R社702.4万円で差は1.3万円である。
共変量の影響を取り除いた調整済み平均をみると、Q社696.8万円、R社703.5万円でその差は6.7万円と差は大きくなった。p値=0.3727>0.05でQ社とR社の平均年収は差があるといえない。

