共分散分析(ANCOVA)≪ 4/4 ≫
回帰係数有意性の検定を解説

fa → 1に 固定
fe → n-群数-1
Sa → 個別回帰式群合算Syy偏差平方和」-「共通回帰式残差平方和」
注.「個別回帰式群合算Syy偏差平方和」 → <3群データ>個別回帰式※1の値
Se → 「共通回帰式残差平方和」
Va → Sa÷fa
Ve → Se÷fe
F → Va÷Ve
p値 → Excel関数 =FDIST(分散比F,fa,fe)
判定 [**] p値≦0.01 [ *] 0.01<p値≦0.05 [ ] p値>0.05
3群データの回帰係数有意性の検定結果は下記の通りである。

上記表の計算方法を示す。
fa → 1 固定
fe → 31-3-1=27
Sa → 28817.5-7568.56=21248.99
Se → 7568.56
Va → 21248.99÷1=21248.99
Ve → 7568.56÷27=280.32
F → 21218.99÷280.32=75.80
p値 → Excel関数 =FDIST (75.80,1,27) Enter 0.0000
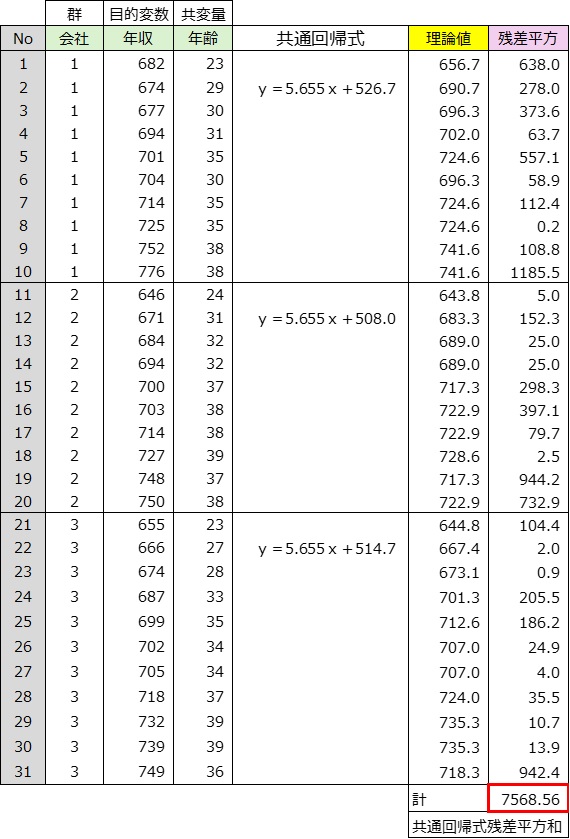
共通回帰式残差平方和の求め方
共通回帰式に年齢を代入し理論値を算出する。
例 No1の理論値 y=5..655×23歳+526.7=656.7
No1の残差平方 (No1年収実績値-No1理論値)2=638.0
31人の残差平方を合計する。この値が共通回帰式残差平方和である。
回帰係数平行性の検定を解説

fa → 群数—1
fe→ n-2×群数
Sa→「共通回帰式残差平方和」-「個別回帰式残差平方和」
注.:「共通回帰式残差平方和」 → 「回帰係数有意性の検定を解説」の
「共通回帰式残差平方和の求め方」表内赤枠 参照
「個別回帰式残差平方和」 →「回帰係数平行性の検定」の
「個別回帰式残差平方和の求め方 」表内赤枠 参照
Se→「個別回帰式残差平方和」 → 「回帰係数平行性の検定」の
「個別回帰式残差平方和の求め方 」表内赤枠 参照
Va→ Sa÷fa
Ve→ Se÷fe
F→ Va÷Ve
p値→ Excel関数=FDIST(分散比F,fa,fe)
判定 [**] p値≦0.01 [ *] 0.01<p値≦0.05 [ ] p値>0.05
3群データの回帰係数平行性の検定結果は下記の通りである。

fa→ 3-1=2
fe→ 31-2×3=25
Sa → 7568.6-7543.96=24.60
Se → 7543.96
Va →24.60÷2=12.30
Ve→ 7543.96÷25=301.76
F → 12.30÷301.76=0.0408
p値→Excel関数で =FDIST (0.0408,2,25) Enter 0.9601
個別回帰式残差平方和の求め方
個別回帰式に年齢のデータを代入し理論値を算出する。
残差平方は(年収データ-理論値)の2乗である。
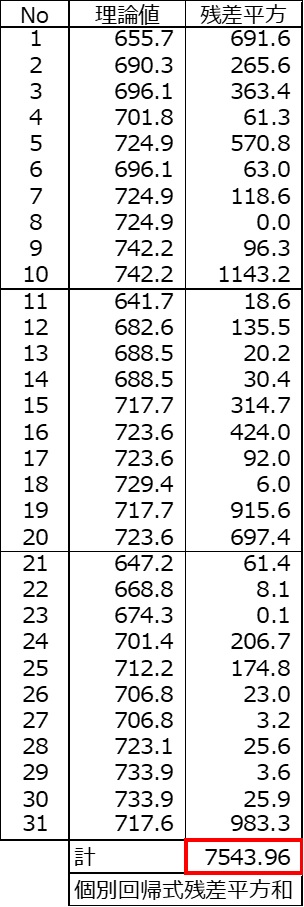
<計算例>
No2 理論値
群1 P社の個別回帰式 y=5.766x+523.1
y=5.766×29歳+523.1=690.3
残差平方=(年収データ-理論値)2
=(674-690.3)2=265.6
No12 理論値
群2 Q社の個別回帰式 y=5.850x+501.3
y=5.850×31歳+501.3=682.6
残差平方=(年収データ-理論値)2
=(671-682.6)2=135.5
No22 理論値
群3 R社の個別回帰式 y=5.421x+522.5
y=5.421×27歳+522.5=668.8
残差平方=(年収データ-理論値)2
=(666-668.8)2=8.1
調整済み平均の有意差検定を解説
<3群データ>調整済み平均の有意差検定の表を再度下記に示す。

調整済み平均の有意差検定の統計量の求め方を解説する。
統計量は次に示す方法でデータを作成し、このデータに重回帰分析を行うことによって求められる。
重回帰分析は(群数-1)ケース行う。この例は3群なので重回帰分析は2ケース行う。
したがって、データも2ケース作成する。
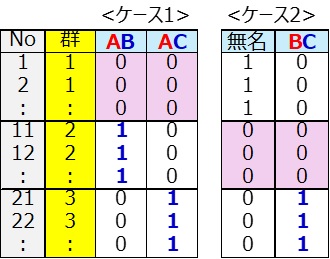
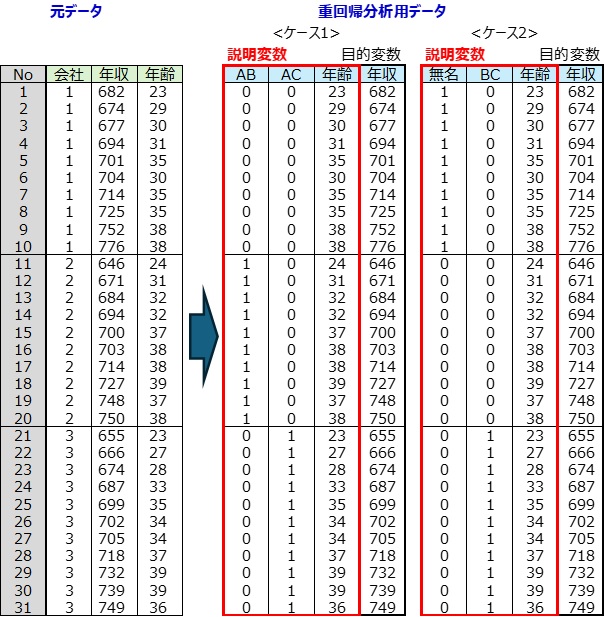
<ケース1>のデータ
目的変数 年収データ
説明変数 群データ(会社)を1,0データに変換した2項目と年齢データとする。
1,0データの項目名はAB、ACとする。
<ケース2>のデータ
目的変数 年収データ
説明変数 群データ(会社)を1,0データに変換した2項目と年齢データとする。
1,0データの項目名は、無名、BCとする。
<ケース1>
・ 項目名をAB、ACとする。(英字がある項目名の先頭すべてA)
・ AB、ACは項目名先頭にAがあるので、群1(A)の塊は全て0。
(ピンク色)
・ AB列 → ABは項目名後ろにBがあるので、群2(B)の塊は1。(紺色)
・ AC列 → ACは項目名後ろにCがあるので、群3(C)の塊は1。(紺色)
・その他のセルはすべて0とする。
<ケース2>
・ 項目名を無名、BCとする。(英字のある項目名の先頭はB)
・ BCは項目名先頭にBがあるので、群2(B)の塊は全て0。(ピンク色)
BCの項目名後ろにCがあるので、群3(C)の塊は1。(紺色)
・その他のセルはすべて0とする。
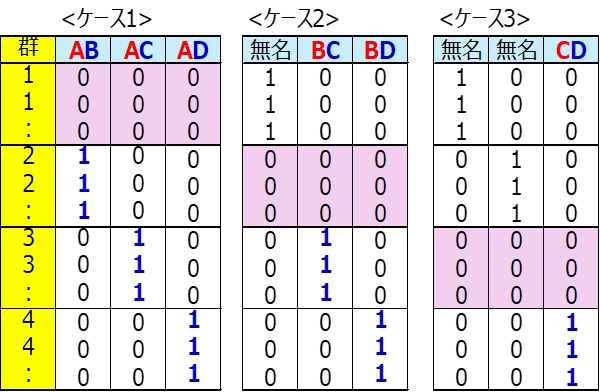
この例は3群だが4群(A、B、C、D)の場合の1,0データの作成方法を示しておく。
群数4なので重回帰分析用データは3ケース(群数-1)作成。
・群1をA、群2をB、群3をC、群4をDとする。
<ケース1>
・項目名をAB、AC、ADとする。(英字がある項目名の先頭すべてA)
・AB、AC、ADは項目名先頭にAがあるので、群1(A)の塊は全て0。(ピンク色)。
・ABは項目名後ろにBがあるので、群2(B)の塊は1。(紺色)
・ACは項目名後ろにCがあるので、群3(C)の塊は1。(紺色)
・ADは項目名後ろにCがあるので、群4(D)の塊は1。(紺色)
・その他のセルはすべて0とする。
<ケース2>
・項目名を無名、BC、BDとする。(英字がある項目名の先頭すべてB)
・BC、BDは項目名先頭にBがあるので、群2(B)の塊は全て0。(ピンク色)。
・BCは項目名後ろにCがあるので、群3(C)の塊は1。(紺色)
・BDは項目名後ろにDがあるので、群4(D)の塊は1。(紺色)
・その他のセルはすべて0とする。
<ケース3>
・項目名を無名、無名、CDとする。(英字がある項目名の先頭はC)
・CDは項目名先頭にCがあるので、群3(C)の塊は全て0。(ピンク色)。
・CDは項目名後ろにDがあるので、群4(D)の塊は1。(紺色)
先の3群データの重回帰分析用データを示す。
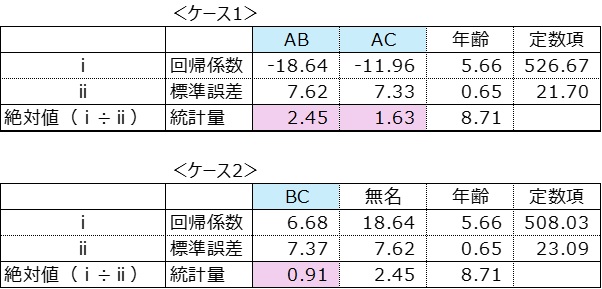
重回帰分析の結果を示す。
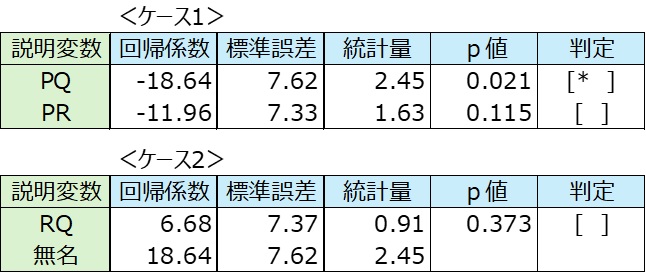
p値
統計量はt分布に従う。
p値はExcel関数で求められる。
自由度=個体数-群数-1=31-3-1=27
Excel関数 =TDIST(統計量、自由度)
ABのp値 =TDIST(2.45,27) Enter 0.0213
ACのp値 =TDIST(1.63,27) Enter 0.1146
BCのp値 =TDIST(0.91,27) Enter 0.3727
切片が異なるか否かの検定 (水準間の差の検定)を解説
調整済み平均の有意差検定を行う前に実施すべき検定が「切片が異なるか否かの検定」である。
下記は「別の事例」ページで示した図である。
切片が異なるか否かの検定の結果を示す。

p値>0.05より、3群の調整済み平均は同等であるといえる。
p値≦0.05となった場合、3群の調整済み平均は同等でないといえる。
この場合、先に示した3群間相互の調整済み平均の有意差検定を実施する。
留意点1 「切片が異なるか否かの検定」では、3群の調整済み平均は同等であるといえる。
先の「調整済み平均の有意差検定」ではPとQで有意差が見られた。
留意点2 このように、両者の検定で結論が異なることがあり、「切片が異なるか否かの検定 (水準間の差の検定)」
をせず、ダイレクトに「調整済み平均の有意差検定」を見るのが良いとされている。
「切片が異なるか否かの検定」を適用する場面はほとんどないが、この検定の計算方法を示しておく。
下記は、「<2群データ>調整済み平均の算出の考え方」で示した図である。
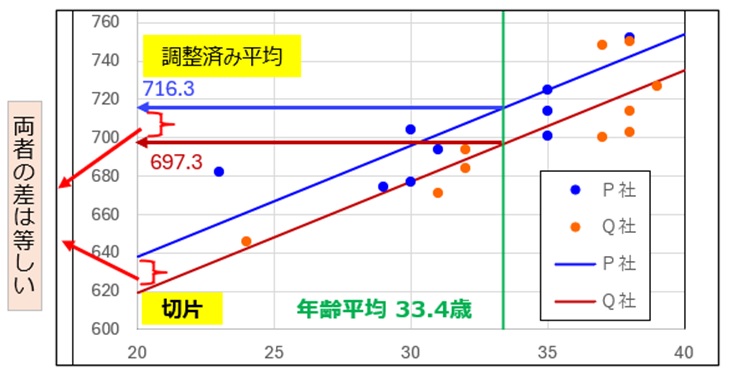
調整済み平均の差分は、共通回帰式と縦軸切片との交点から作られる差分と同じである。
したがって、切片の差が異なれば、調整済み平均の差も異なるがいえる。

fa → 群数-1
fe → n – (1+ 群数)
Sa → 「全体回帰式偏差平方和」-「共通回帰式残差平方和」
注.:「全体回帰式偏差平方和」 → 下表「全体回帰式残差平方和の求め方」赤枠参照
「共通回帰式残差平方和」→「回帰係数有意性の検定を解説」の
「共通回帰式残差平方和の求め方」表内赤枠 参照
Se → [共通回帰式残差平方和」
注:「回帰係数有意性の検定を解説」の「共通回帰式残差平方和の求め方」表内赤枠 参照)
Va→ Sa÷fa
Ve→ Se÷fe
F→ Va÷Ve
p値→ Excel関数=FDIST(分散比F,fa,fe)
判定 [**] p値≦0.01 [ *] 0.01<p値≦0.05 [ ] p値>0.05
3群データにおける切片が異なるか否かの検定の結果を再度示す。

fa → 3-1=2
fe → 31-(1+3)=27
Sa → 9297.9-7568.6=1729.33
Se → 7568.6
Va → 1729.3÷2=864.67
Ve → 7568.6÷27=280.32
F → 864.67÷280.32=3.08
p値 → Excel関数 =FDIST (3.08,2,27) Enter 0.0622
全体回帰式残差平方和の求め方
全体回帰式に年齢のデータを代入し理論値を算出する。
残差平方は(年収データ-理論値)の2乗である。
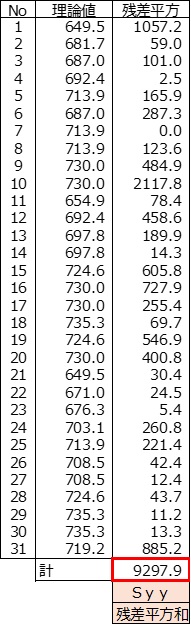
<計算例>
No2 理論値
全体回帰式 y=5.366x+526.06
y=5.366×29歳+526.06=681.7
No2 残差平方
残差平方=(年収データ-理論値)2
=(674-681.7)2=59.0

