統計探偵物語　第1話

偏差値について学ぶ

依頼人　

　第1話は、雪乃が統計探偵事務所に入社してもまないころ、所長からいろいろ教えてもらいながら、初めてした仕事のお話である。

依頼主：　「こんにちは。平日の朝6時から8時まで放送しているテレビワイド番組「モーニングトップ」をご存知でしょうか。私は番組の企画を担当している鈴木です。」

依頼内容

鈴木：　「 この番組はプロ野球チーム『宇宙ジャガーズ』を応援しています。
そこで、このチ－ムで毎月バッターとして最も活躍した選手に賞金を出すことにしました。
打率、ホームラン数、打点の３つで総合成績を出し、最も成績の良い選手を選びたいと思います。
どのようにすれば総合成績を出せるか教えてください。」

所長：　「 一ヵ月間に１0試合以上プレーした選手の打率、ホームラン数、打点の成績を教えてください。」
鈴木：　「これでよいですか。」

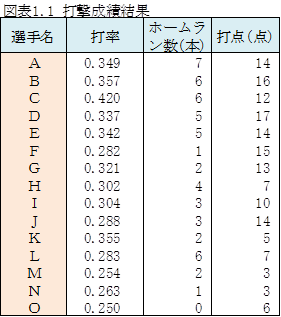
所長：　「はい。このデータに基づき、『 最も活躍した野球選手は誰か 』を決める方法を提案させていただきます。統分雪乃が提案書を作成します。3日間お時間をください。」
雪乃：　（ヒャー私に、できるのかしら。）

鈴木：　「料金はいかほどで」
所長：　「提案書の内容にご満足いただけたら10万円をお支払ください。
鈴木：　（こんな若い女子にできるのかなと思いつつ）「よろしくお願いします。提案書が完成したらご連絡ください。」

単位が異なるデータ「打率」「ホームラン数」「打点」の比較

雪乃：　「所長が教えてくれないと、私なにもできません。」
所長：　「何をあまったれたこと言っているんだ。やるのは君だ！」

雪乃：　「は、はい。私はあまり野球には詳しくないのですが、3つの打撃部門のデータは単位が違いますよね。」
所長：　「そうだよ。打率は打数に対する安打（ヒット）の割合で、テレビや新聞では何割何分何厘と言われている。ここでは小数点で表記されているね。ホームラン数は「本」、打点は「点」で雪乃の言う通り、データの単位が異なるね。」

雪乃：　「ということは、3つの成績を合計して、値が最も大きい選手を選ぶというわけにはいきません。」
所長：　「雪乃がデータ単位の異なる項目を合計する方法を考えるんだ。」

雪乃：　「打率、ホームラン数、打点それぞれについて、順位を調べました。
打率では、1位がＣの0.420、2位がＢの0.357、･･･です。
ホームラン数では、1位がＡの7本、2位がＢ，Ｃ，Ｌの6本、次に続くのがＤ、Ｅの5本ですが、1位と2位に4人いるので5位としました。
打点では、1位がＤの17点、2位がＢの16点、･･･です。そして、各選手について順位の合計を求めてみました。」

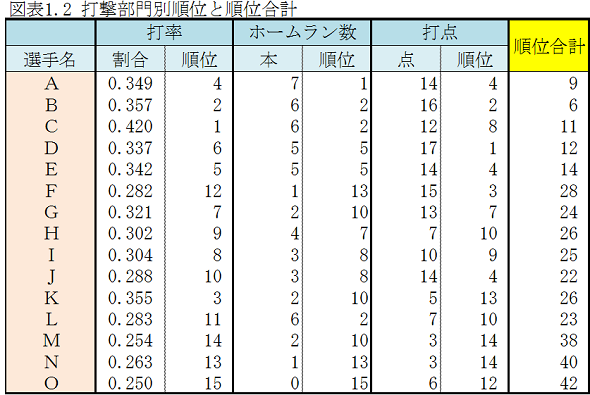
所長：　「結論は？」
雪乃：　「順位合計の値が最も小さい選手はＢ選手、次にＡ選手、Ｃ選手が続きます。だから総合成績１位はＢ選手じゃないですか？」

所長：　「順位の合計を求めたことはすばらしい。だが、順位合計には少し問題があるんだ。」
雪乃：　「どんな問題があるのですか？」

所長：　「そのことを解答する前に、雪乃に質問だ。各打撃部門で成績の最も良い1位の選手を調べると、打率は0.42のＣ選手、ホームラン数は7本のＡ選手、打点は17点のＤ選手だね。」
雪乃：　「はい、その通りです。」

所長：　「それぞれ1位の打率0.42、ホームラン数7本、打点17点を比較したとき、雪乃はどれが１番よい成績だと思う？
どれも1位だけど、ひとつ選んでみてよ。」
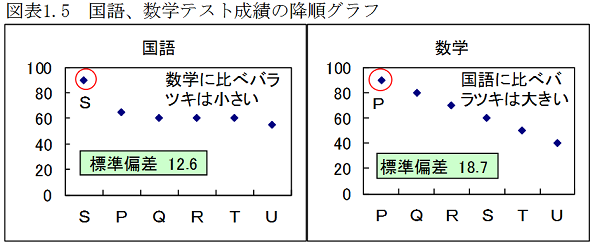
雪乃：　「よく分からないけれど、データを降順に並べ替えたグラフを作ると、2位以下を大きく引き離しているＣの打率0.42が一番良いように思えます。」

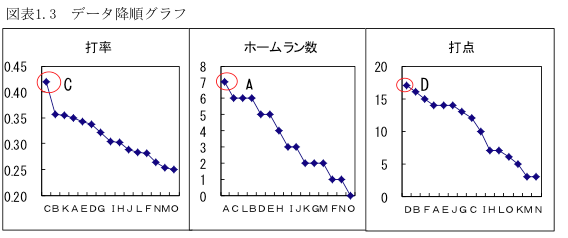
所長：　「データの降順グラフを描いて調べるとはいいセンスをしているね。」
雪乃：　（ウフフ、嬉しいつぶやき）

別データによる検証：国語90点の生徒S・数学90点の生徒Pとでは、どちらに価値がある？

所長：　「ここでさらに、雪乃に質問だ。野球とは別のデータ、例えば国語と数学のテストの成績が次だったとする。国語で90点の生徒Ｓと数学で90点の生徒Ｐとでは、どちらの方に価値があるかという問題だ。」

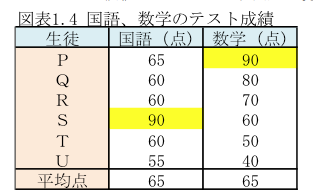
雪乃：　「平均点は、国語と数学どちらも65点で同じですね。だから平均点との差はどちらも25点なので、国語の90点と数学の90点の価値は同じではないですか？」

所長：　「バカモン。さっき、グラフで2位以下との差を比較して判断しただろう。」
雪乃：　「そうですね。先ほどと同じ考え方でいくと、国語は2位の65点との差が25点、数学は2位の80点との差が10点なので、国語の90点の方が数学の90点より価値があるといえます。」

所長：　「そのとおりだ。正解だけど、実際は2位との差だけで判断するのではない。データのバラツキを考慮して正解を導くんだよ。」
雪乃：　「データのバラツキって何ですか？」

所長：　「アチャチャー。データのバラツキを表す標準偏差を知らないのかい。」
雪乃：　「はい、知りません。」

所長：　「シンジラレナーイ」
雪乃：　（所長のいやみの言葉は無視して）「教えてください。」
所長：　「いやだね。インターネットで標準偏差を検索して勉強しろ。」

データのバラツキを表す標準偏差

雪乃は標準偏差をインターネットで調べ、Excelで簡単に計算できることを知った。

雪乃：　「標準偏差の計算って簡単でした。国語の標準偏差は12.6点、数学は18.7点です。だから、データのバラツキは国語の方が数学より小さいです。」
所長：　「計算の仕方だけでなく、標準偏差の意味も分かっているな。」

雪乃：　「はい。国語は1位が90点と高いけど他の生徒は55点から65点とバラツキの幅が小さく、6人全体のバラツキは小さいです。数学は1位が90点、次に80点、70点と高得点が続きますが、40点と低い得点の人もいて6人全体のバラツキは大きいです。このバラツキの大小を表したのが標準偏差です。」

所長：　「そうだね。国語はバラツキが小さい、すなわち大半の人が55点から65点の中で、90点を取るのは難しい。数学はバラツキが大きい、すなわち、40点と低い点数もいるけど70点や80点と高い点数もいるので数学では90点を取りやすいといえるんだ。」

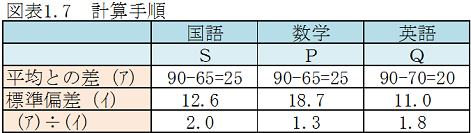
所長：　「このことは、雪乃が求めた標準偏差を用いて、次の計算をするとより明確となるよ。
(A)は7.1、(B)は4.8で、(A)は(B)より大きく、国語の方が価値があるといえる。」

(A)国語90点÷国語の標準偏差＝90÷12.6＝7.1
(B)数学90点÷数学の標準偏差＝90÷18.7＝4.8

雪乃：　「私が、国語の90点が他に比べて突出して高いと思ったのは、言い換えればバラツキの小さいデータの中で90点とったという判断だったのですね。だから標準偏差の値が小さい国語の方が価値があったということですね。」

所長：　「すごいじゃないか。よくわかったね。」
雪乃：　（ヤット理解できたのだけどすました顔で）「簡単でした。」

平均値・標準偏差がわかれば、データを偏差値にすることにより、集団での位置を把握できる

所長：　（この子は思ったより使えるかも、さらに難しい質問をしてみるか）「数学と国語は平均点が同じだが、例えば平均点が異なる英語を加えてみよう。国語90点、数学90点、英語90点ではどれが一番価値があると思う？」

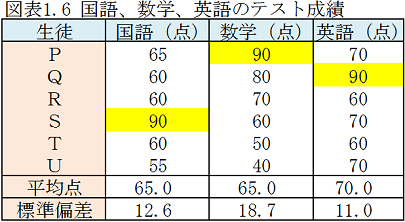
雪乃：「エーと、平均点に比べ何点高いかを調べます。求められた値を標準偏差で割ればよいと思います。計算すると国語のＳの90点の値は2.2で、一番良いと思います。」

所長：　（ここで褒めたいところだが、褒めると調子にのるので）「このくらいのことが理解できて当然だ。」
雪乃：　（いつも所長のきつい目が柔らかくなっている　合格点をもらえたみたい）

所長：　「雪乃が求めた値を統計学では基準値というんだ。」
雪乃：　「テスト成績を基準値で表す方法、よくわかりました。基準値は1位の90点だけでなく、2位以下の得点についても求められますよね。」

所長：　「当然だ。全ての生徒について求めてごらん。」
雪乃：　「基準値を計算しました。」

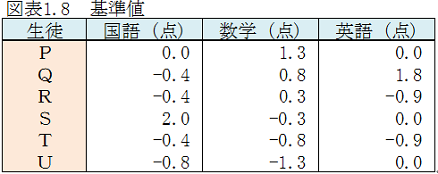
雪乃：　「国語の成績が0.0点とか数学が1.3点とか言われてもピンときません。」
所長：　「そうだね。テスト成績などは基準値でなく偏差値を用いるんだ。偏差値は基準値を10倍して50を足すんだ。」
雪乃：　「例えば、数学のＰさんの1.3の偏差値は10×1.3+50＝63でよいですか。」

所長：　「その通り。」
雪乃：　「あの有名な偏差値。私を苦しめたあの憎き偏差値って、このようにして求めるんですか。」

所長：　「そうだ。偏差値って有名用語だけど、求め方を知っている人はあまりいないね。」
雪乃：　「学生時代、偏差値を知っていれば、偏差値を高めることができたのに残念です。」

所長：　「それはあまり関係ないよ。」
雪乃：　（まーね）
所長：　「全ての生徒の偏差値を求めてごらん。」
雪乃：　「求めました。」

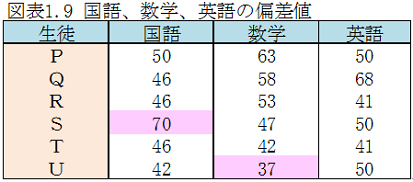
所長：　「偏差値は全ての値を比較できる。一番良いのは国語Ｓの70、一番悪いのは数学Ｕの37である。
雪乃：　「はい、すばらしいです」

所長：　「偏差値の平均点を求めてごらん。」
雪乃：　「偏差値の平均値を求めたら、どの科目も50になりました。」

所長：　「だから全ての偏差値を比較できるんだ。雪乃の偏差値はどのくらいだった。」
雪乃：　「55ぐらいでした。」

所長：　「すごいじゃないか。50を超えているのは、平均より上、1万人の受験生がいれば大雑把にいって5000番以内に入っていることだよ。」
雪乃：　（ウフフ,私ってすごいのね）

調査結果

所長：　「それでは鈴木さんから頼まれた仕事をしておいてね。」
雪乃：　「求めました。偏差値を求めるだけでなく、偏差値の合計を求め、合計が最も大きい選手を調べました。」

所長：　「ホー、それで。」
雪乃：　「Ｃ選手に賞金をだすのが良いと思います。」

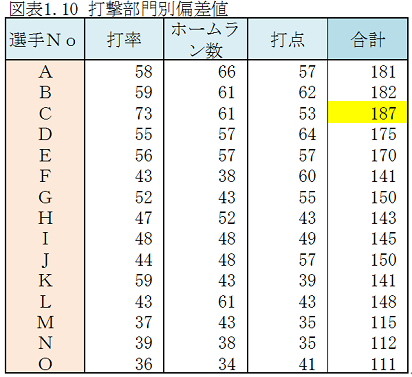
所長：　「よくできたね。雪乃が最初に求めた順位の合計と比較してごらん。」

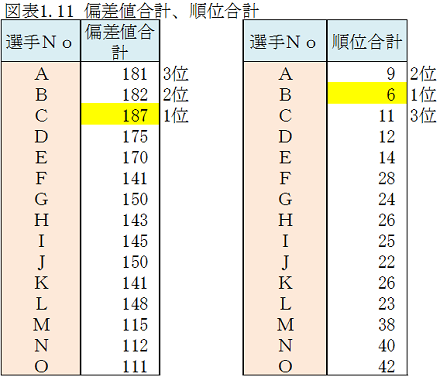
雪乃：　「順位合計では1位がＢ選手でした。」

所長：　「優秀選手を決めるのにどちらの方法が良いかという統計学的基準はないんだ。だからどちらを使ってもよいのだが、鈴木さん始め、選手、テレビ視聴者が納得する方法が最良といえる。ぼくは皆が納得するのは順位合計でなく偏差値合計だと思う。」

雪乃：　「用いる方法によって賞金をもらえる選手が変わってしまうので、分析する人の責任は重大ですね。」

所長：　「そうだよ。雪乃は、鈴木さんに偏差値合計で優秀選手を決めたことをきちんと説明し、納得させなければいけないよ。それができて仕事が完了なんだ。」
雪乃：　「私にできるかしら。頑張ります。」

依頼人への報告

後日談、雪乃が得意顔で企画担当者鈴木さんに説明

雪乃：　野球選手が多数いる中で個々の選手の打撃成績がどのような位置にあるか」、すなわち、「集団の中で個々のデータがどのような位置にあるか」を把握したいとき、全てのデータを眺めながら一つ一つ位置関係を決めていくのは大仕事です。
けれども平均値や標準偏差が分かっていれば、データを偏差値にすることによって集団での位置が把握できます。

偏差値の公式は、【10×（データ－平均値）÷標準偏差＋50】です。

『偏差値で野球選手を評価』というキャッチフレーズで放映します！と、喜んで帰っていった。

第1話　終わり