
直線回帰分析について学ぶ
依頼内容
第4話は、雪乃が少しではあるが統計解析に自信を持った時、常夏市環境課の担当者から受けた依頼がテーマである。
依頼主:「こんにちは。常夏市環境課の佐藤です。」
雪乃: 「統分雪乃です。よろしくお願いします。」
佐藤: 「早速ですが、お願いしたいテーマをお話しします。」


我が常夏市の8月の平均気温は、過去30年で3度の上昇がみられ、他の都市に比べて大きな上昇です。
気温上昇の原因には、地球温暖化の影響もありますが、ヒートアイランド現象を含む都市温暖化の傾向が、顕著に現れています。何も対策をたてずにいると、この傾向が増加し30度ラインを超えてしまうことを、市議会に提示したいと思います。お願いしたいことは、常夏市の10年後の平均気温がどうなるかを推計していただくことです。
 雪乃
雪乃「常夏市の気温データをいただけますか。」



「こちらのデータでよろしいですか。」
(図表1参照)
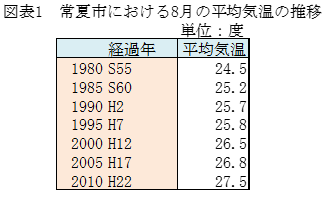




「はい、このデータから2015年と2020年の8月の平均を推計させていただきます。結果がでましたらご連絡させていただきます。」
この案件については、雪乃は1人で分析しようと思ったが、結局は所長の力を借りながら分析することになった。
関数式のあてはめ



「縦軸(Y軸)を平均気温、横軸(X軸)を経過年にとり、折れ線グラフを描きました。そして折れ線グラフの真ん中を通る直線を引きました。」
(図表2参照)
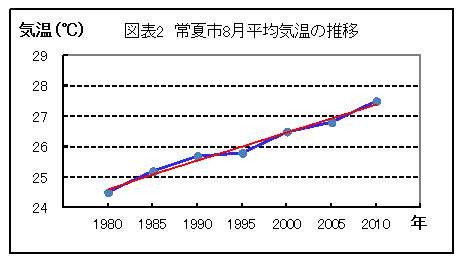




「そしてどうしたの?」



「この直線の傾向通りに平均気温が推移するとすれば、2015年、2020年の平均気温はこの直線上にあるということで、次のようにして2015年、2020年の平均気温を求めました。」(図表3参照)
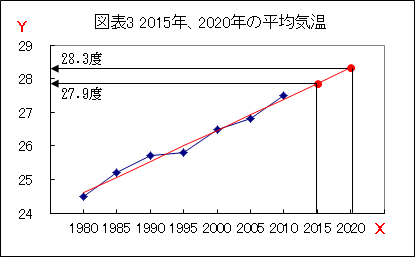




「予測値を求める考え方はよいけど、直線の引き方に疑問を感じるね。」



「やっぱり、真ん中を通る直線を適当に引いたのはまずいですね。」



「そうだ。図表4のように直線は引こうと思えば何本でも無数に引けるよね。どの直線が良いか理論的に説明できないとお客様は納得しないよ。
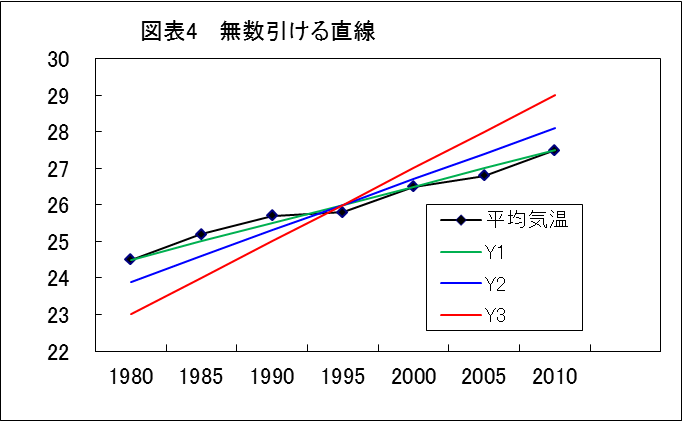




「どのような考え方で直線を引くのか教えてください。」



「図表5に示すように、点から直線「Y3」までの差を計算し、その2乗を求めるんだ。」
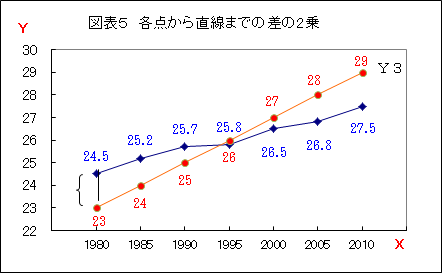




「分かりました。(カチカチカチ・・)
全ての点について、直線「Y3」との差の2乗を求めました。」(図表6参照)





「差の2乗の合計はいくつかな。」



「8.16です。」



「この値を残差平方和というんだ。」



「残差平方和を計算するとき、なぜ差の2乗をするんですか。」



「差の合計だと、いかなる場合も0になるので、残差平方和は差の2乗の合計なんだ。」



「なるほど、よく分かりました。」



「他の直線Y1、Y2についても残差平方和を求めてください。」



「求めました。」
(図表7,8参照)
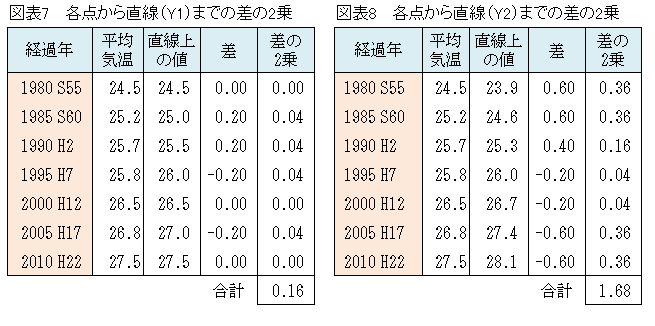




「残差平方和が最小となる直線はどれかな。」
(図表9参照)





「Y1です。」



「【図表4 無数引ける直線】と【図表9 各直線の残差平方和】と突き合わせて見てください。平均気温の各点が直線に近いのはY1だ。このY1の残差平方和が最も小さいよね。」



「はい、その通りです。」



「残差平方和が最小となる直線が最適な直線といえるんだ。」



「分かりました。」



「このような考え方で直線を導く方法を、最小二乗法というのだ。」



「考え方はわかりましたが、いくつもの直線について残差平方和を求めるのは大変な作業になります。もっと簡単な方法で直線を求める方法はないのでしょうか。」



「あるよ」



(もぉう~それなら最初から教えてくれればいいのにと思いつつ)
「教えてください。」



「図表1においては、経過年が決まれば平均気温がピッタリ決まるという関係が見られない。だから経過年と平均気温の関係を、関係式で表すことはできないんだ。」



「よく分からないけど、私の大好きな『あんまん』と購入金額の関係は、1個で100円、2個で200円、3個で300円、・・・、のような関係がないということですよね。」





「『あんまん』ときたか。そうだよ、『あんまん』の個数が決まれば購入金額がピタリと決まる。だから、購入金額=100円×『あんまん』個数という関係式で表せる。経過年と平均気温はこのような関係式で表せないということだ。」



「わかりましたけど、だから何なの。」



(”だから何なの”に、くじけそうになる所長・・・)
「『あんまん』と購入金額のような関係はないものの、年が経過するにつれ平均気温が高まる、という傾向が図から見ることができる。だから、経過年と平均気温はまったくの無関係であるともいえないんだ。」



「そうですね。」



「このような2つの事柄(変数)、例えばXとYについて、Xの値が決まればYの値が決まるというわけでないが、両者の間になんらかの関係が見られるとき、適当な直線を決めてあげれば、Xの値に対してYの平均的な値を推定することができる。
このように直線をあてはめることを「関数式のあてはめ」といい、その方法は回帰分析という解析手法で行なうことができるんだ。」



「わざと説明を難しくしているみたいですけど、理解はできました。」



「回帰分析は色々な分野で適用されるが、直線のあてはめで回帰分析を用いる場合、直線回帰分析という。」



「直線の式はY=aX+bでしたよね。」



「そうだよ。Y3の直線の式は?」



「エーット。」



「うろ覚えではいかんぞ。」



「あちゃぁ~」



「実はこの問題は易しそうで難しいんだ。
経過年は2010やH22で表されている。
これらは経過年の名称で数値データではない。
経過年は数値データに置き換えるんだ。
一般的には1から始まる整数1,2,3,4,・・・を適用する。
この整数を時間変数と呼ぶことにしよう。(図表10参照)
この表のグラフを描いてください。」
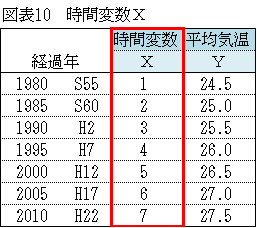




「描きました。」
(図表11参照)
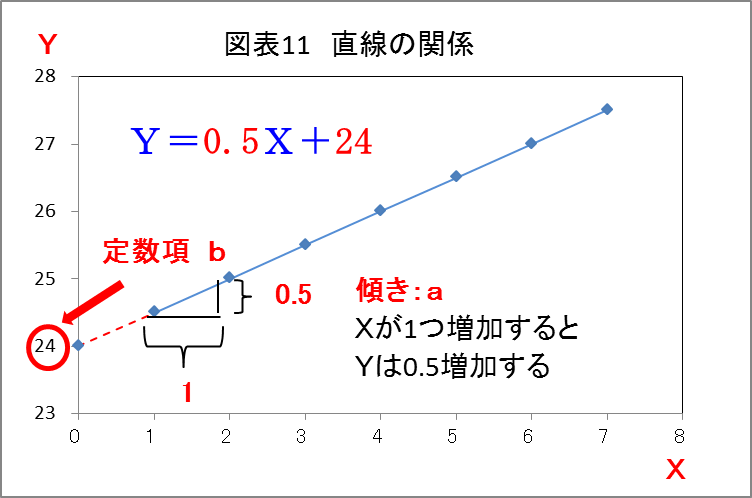




「Xが0のとき、Yの値はいくつかな。」



「直線が縦軸と交わるところの値ですね。24です。」



「その値がY=aX+bのbの値だ。」



「aは直線の傾きと覚えていましたので、0.5ですよね。



「OK」
「それでは、残差平方和が最小となる直線Y=aX+bのaとbの求め方を教えよう。
いつだったか、雪乃君の学生時代の友人美咲さんから相談された件で、単相関係数を適用したよね。」
第2話 「練習するほど腕立て伏せの回数は増えるといえるかを教えて」を参照



「はい、単相関係数を使いました。」



「平均気温と時間変数Xの単相関係数を算出してください。」



「単相関係数の計算手順にしたがい「図表12」を作成しました。」
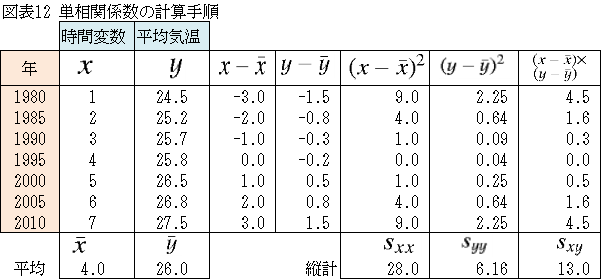




「単相関係数の公式に基づき計算すると、単相関係数は0.9899となりました。」
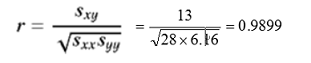
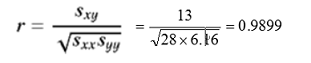



「ご苦労さん。単相関係数を求めてもらったけど、残念ながら、今回は使わないよ。」



「そんなー」



「計算手順表の作成は無意味でないよ。aは次の公式で求められるよ。」
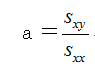
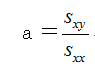



「ということは13÷28で、aは0.4643ですね。」



「bの求め方を説明しよう。bは次の式で求められる。」
b=平均気温の平均 - a × 時間変数Xの平均



「計算手順表から平均気温の平均は26、時間変数Xの平均は4だから、
b=26-0.4643×4=24.14 です。」



「OK、それではこの関係式にX=1,2,3,4,5,6,7を代入し、Yの値を求めてください。」



「計算しました。」
(図表13参照)





「求めたYの値と平均気温のグラフを描いてください。」



「描きました。」
(図表14参照)
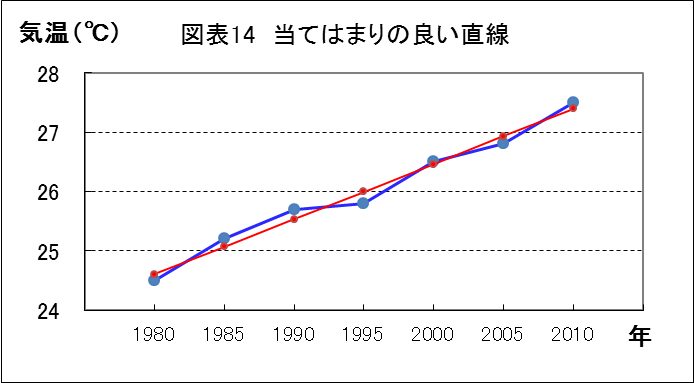




「グラフの直線が最も当てはまりの良い直線ということだよ。」



「直線の残差平方和を求めてみます。」



「0.12です。先ほどはY1の残差平方和が0.16でしたが、さらに小さくなりました。」
(図表15参照)
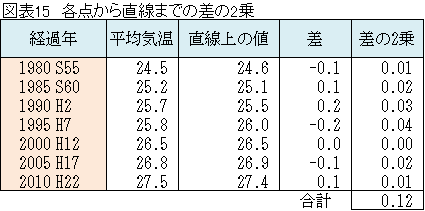




「図表12を適用し、a、bの算出公式から導かれた直線が、最も当てはまりのよい直線になることは数学的に証明されているんだ。
ここでは省略しよう。」



「了解です。」



「求められた直線に2015年、2020年の時間変数Xの値を代入すれば、2015年、2020年の平均気温が予測できるよ。」



「2015年、2020年の時間変数は8と9でよいですか。」





「OK」



「2015年は27.9度、2020年は28.3度です。」
(図表16参照)
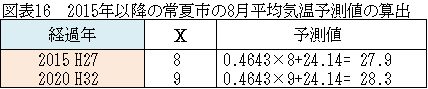




「ばっちりじゃないか。この結果をきちんと常夏市環境課の佐藤さんに説明できるかテストしよう。」



「そんなー。」
他市の平均気温のデータでも直線回帰分析を行ってみる



「他市の平均気温のデータがある。(図表17参照)
この市の平均気温は上下変動して推移している。
このデータに直線回帰分析を行い、直線式、残差平方和を求め、平均気温の推移に直線を引く。そして2015年、2020年の平均気温を予測するというテストだ。」





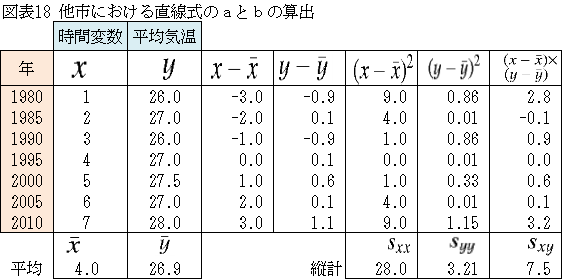
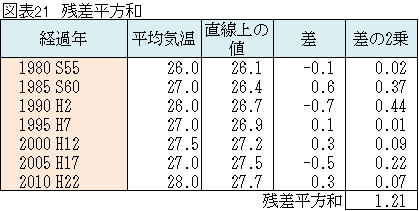
「できました。」(図表18~22参照)

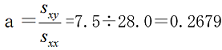
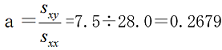
b=平均気温の平均 - a × 時間変数Xの平均
=26.9-0.2679×4.0 =25.86
直線式 Y=0.2679X+25.86


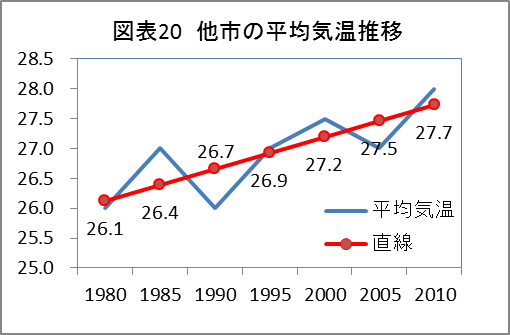







「よくできた、合格だ。」



「嬉しいです。」



「残差平方和は1.21(図表21参照)で、常夏市の残差平方和0.12に比べ大きいが、その理由は?」



「他市の平均気温は上下に大きく変動して推移しているから、直線の当てはまりが悪いのだと思います。」



「そこでだ。残差平方和のSyy(平均気温の偏差平方和)に占める割合を計算するんだ。」



「常夏市について求めてみます。Syyは6.16、残差平方和は0.12だから、0.12÷6.16=0.02です。」



「他市は?」



「Syyは3.21、残差平方和1.21だから、1.21÷3.21=0.38です。」



「この値が小さいほど当てはまりが良いことは分かるよね。」



「はい」



「この値を定数1から引いた値が有名な決定係数なんだ。」



「ということは、常夏市の決定係数は1-0.02=0.98、
他市の決定係数は1-0.38=0.62です。」



「OK」



「決定係数は大きいほど当てはまりが良いということですね。」



「そうだ。決定係数が大きければ2015年、2020年の平均気温予測値は信頼できる数値と考える。」



「決定係数が低いということを私なりに考えてみました。平均気温の推移に直線を当てはめてみたものの、上下変動が大きく推移しているので、『将来の平均気温は求められた直線上にあるといいきるのは危険』である。」



「なかなかいいじゃないか。素晴らしい。」



「決定係数はいくつ以上あれば良いという基準はありますか。」



「統計学的基準はないが、私の経験として0.5以下だと導かれた直線の式は予測には適用できないと思う。」



「常夏市の直線式の決定係数は0.98なので、予測値の精度は高いということですね。」



「その通り。」



「Excelで直線式を求める機能はありますか。」



「あるよ。」



「教えてください。」



「2つの方法があるので、まずは1つ目を教えよう。」
Excelで直線式を求める機能
- 任意のセル(ここではB14)に【=SLOPE】を入力し、()の中でYデータとXデータのセルを範囲指定する。
- 同様に、任意のセル(ここではE14)に【=INTERCEPT】を入力し、()の中でYデータとXデータのセルを範囲指定する。
- Enterキーを押すと結果が出力される。
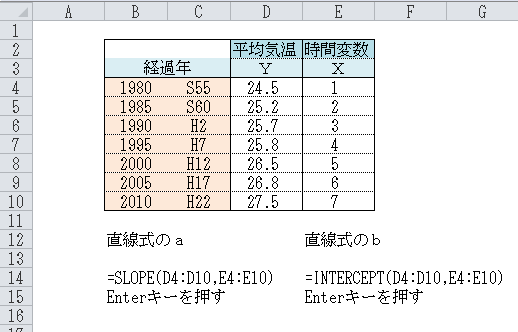

Enterキーを押した出力結果
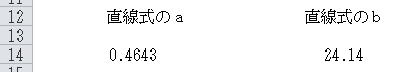
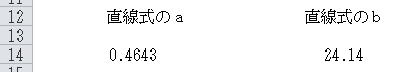
- メニューバー「データ」をクリックする。
- 「データ分析」を選択する。
- 下記の画面で「回帰分析」を選択する。

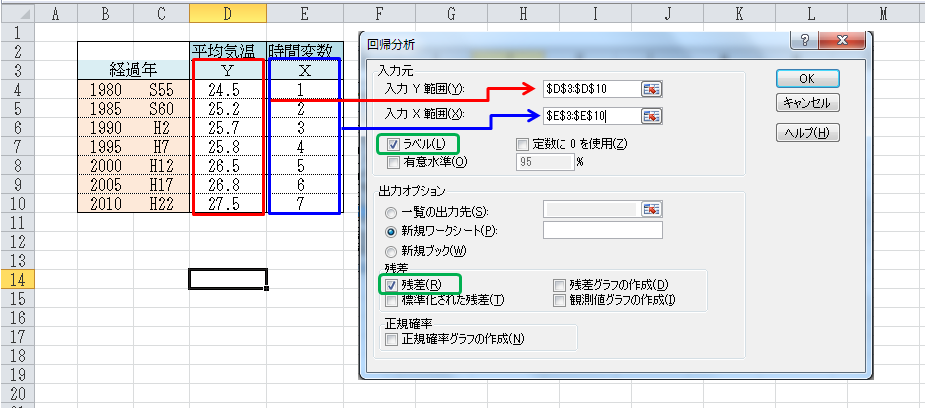
- 下記画面で、YとXのデータを範囲指定する。
- 入力範囲は項目名とデータを指定
- ラベルボタンをチェック
- 残差ボタンをチェック
- OKボタンを押す。

出力結果
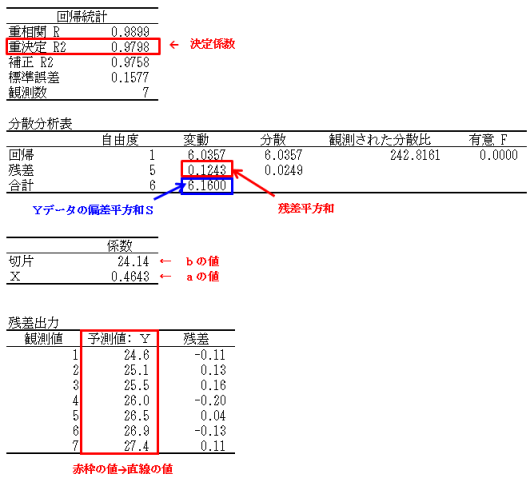




「Excelの回帰分析はよく使うのでしっかりとマスターしておくように。」



「今回は丁寧に教えていただきありがとうございました。」



「はい、がんばります!」
調査報告
数日後、雪乃は今回の結果を報告書にまとめ、常夏市環境課の佐藤さんに報告した。
報告書の内容及び報告の仕方も好評で、お褒めの言葉をいただいた。
第4話 終わり
制作: 菅 民郎
理学博士
株式会社アイスタット代表
ビジジネス・ブレークスルー大学大学院 名誉教授




