信頼区間、有意差検定、P値について学ぶ
依頼内容
第5話は、大学時代のゼミ仲間の田中君と卒業後偶然出会い、調査会社からのアンケート調査結果について相談された件がテーマである。
先週の日曜日、雪乃は大学時代のゼミ仲間の田中君と、卒業後2年ぶりに偶然出会いお茶した。
雪乃が統計探偵事務所に勤めデータ分析の仕事をしていることを伝えると、田中君から「相談料は払えないけど教えて欲しいことがあるんだ。」といわれた。
田中君は月刊誌を出版している会社に勤めている。その月刊誌で主婦のへそくり金額の実態について掲載することになった。調査会社に調査から分析まで全面委託し、田中君が結果を要約し記事を書いた。記事にまとめたものの、統計学のことが分からず調査結果について雪乃に相談したいとのことだった。
田中君から後日、次の資料が送られてきた。
- Wordファイル「調査概要」「結果図」
- Excelファイル「アンケート調査回答データ」
※Excelファイルは、以下の「Excel回答データ.zip」をクリックするとダウンロードできます。
(ファイルはzip形式に圧縮されています。ファイルを開くには、解凍ソフトが必要になります。)


田中君の疑問
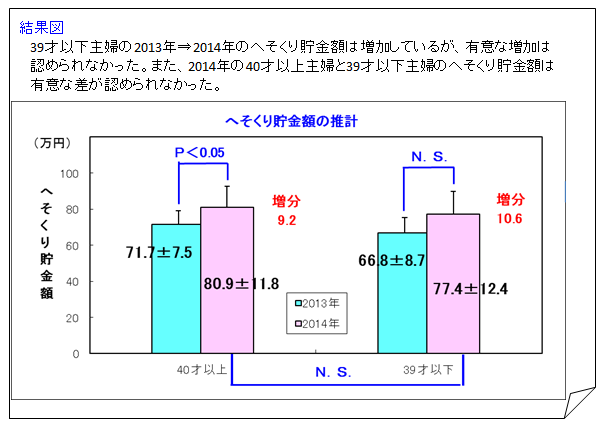
2013年⇒2014年のへそくり貯金額の増加について、「39才以下主婦」の方が増分が大きいのに、有意差は「39才以下主婦」で「ない」、「40才以上主婦」で「ある」という結果になっているのはなぜか。
雪乃の対応
田中君の疑問を解決する前に、雪乃は「P<0.05」、「N.S.」、「±」は見たことはあるが、説明できる知識にいたっていなかった。そこで、所長にお願いし、レッスンしてもらうことになった。
レッスン内容
この図を理解するためには、次の①~⑩のレッスンが必要といわれた。
① 信頼区間とは何だろう
② 「±」とは何だろう
③ 信頼区間は幅が狭いほど推定の精度は良い
④ ヒゲとは何だろう
⑤ 「信頼区間」は○±△を図式化した以上の意味をもつ!
⑥ 標本誤差は主婦数とデータのバラツキから求められる
⑦ 母集団の平均値の違いを測るツール、それがP値
⑧ 「対応のある」、「対応のない」とは何だろう
⑨ 「対応のない」場合の有意差判定
⑩ 「対応のある」場合の有意差判定
① 信頼区間とは何だろう
所長:「2014年のアンケート調査において、40才以上主婦でへそくり貯金をしている人の人数と金額の平均値を教えて?」
雪乃:「人数は49人、金額の平均値は80.9万円です。」
所長:「ところで東京都に居住する40才以上主婦でへそくり貯金をしている人は何人ぐらいいると思う?」
雪乃:「分かりませんけど、数十万人はいると思います。」
所長:「アンケート調査の対象となった49人のデータで、数十万人はいると思われる40才以上主婦のへそくり貯金額平均値は80.9万円といってよいですか?」
雪乃:「いえません。」
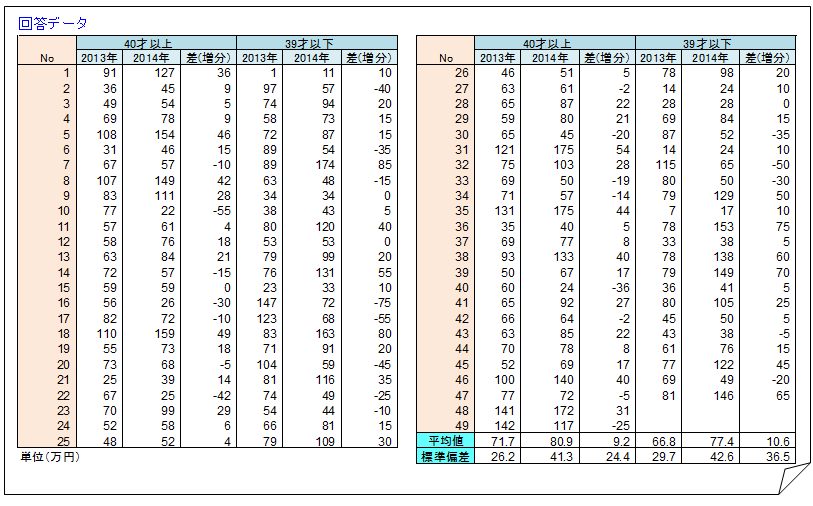
所長:「そうだよね。だから、平均値はほぼこの範囲に収まるという幅を設定するんだ。
具体的にいうと、40才以上主婦のへそくり貯金額の平均値69万円~93万円の範囲にあるというんだ。」
雪乃:「範囲の値はどこから求めたのですか?」
所長:「その幅の求め方が今回のテーマになるので、これから説明するよ。」
所長:「ところで、母集団、標本という単語を知っているかな。」
雪乃:「それくらいは知っています。この例でいえば、母集団は東京都に居住する40才以上主婦でへそくり貯金をしている全ての人。標本はアンケート調査の対象となった49人です。」
所長:「OK。重要なので整理しておこう。」

所長:「母集団全てのデータを集めることは難しく、統計は一部分のデータで全体の傾向を見なければならない。
そこで統計学の考え方では、母集団からランダムに何人かを抽出して平均値を出すんだ。抽出作業を何回か行っても、平均値はほぼこの範囲に収まるという幅を設定する。」
雪乃:「つまり先ほど教えてもらった69万円~93万円の中に何回行っても平均が収まるということですね。」
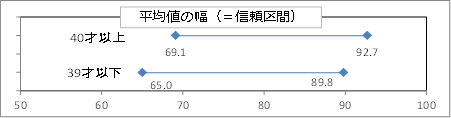
所長:「『何回行っても』というのは正確ではない。一般に統計学の世界では100回行ったら5回くらいはその範囲に収まらなくても信頼性は十分という決まりがある。統計学では『69万円~93万円』を信頼区間(CI,Confidence Interval)という。」
雪乃:「理解できました。」
所長:「この例題の信頼区間を正確に計算すると次になるよ。」
② 「±」とは何だろう
所長:「69.1万円~92.7万円はどうやってだすか考えてみましょう。
49人のデータで、40才以上主婦のへそくり貯金額の平均値を求めると80.9万円です。
ここで平均値に「いくつ」加えると92.7万円になるかな?」
雪乃:「92.7万円から平均値を引けばよいので、11.8万円です。92.7万円-80.9万円=11.8万円」
所長:「平均値から「いくつ」引けば69.1万円になる?
雪乃:「11.8万円です。」
所長:「統計学ではこの値を標本誤差(SE,Sampling Error)という。
標本誤差は統計学の公式によって求められるよ。後で公式を紹介するね。信頼区間は次の式によって求められる。
( 平均値-標本誤差) (平均値+標本誤差) この式をまとめて表記してみて。」
雪乃:「平均値± 標本誤差」
所長:「OK。40才主婦のへそくり貯金額について、この式で表記してください。」
雪乃:「80.9±11.8(万円)です。これが上記の図に示されているんですね。」
所長:「その通り。【平均値±標本誤差】が表記されていれば信頼区間が把握できることは理解できたかな。」
雪乃:「はい。」
所長:「理解したかテストしてみよう。2014年の39才以下主婦の信頼区間を求めてみなさい。」
雪乃:「上記の図をみると、2014年の39才以下主婦は77.4±12.4(万円)だから「77.4-12.4=65.0」「77.4+12.4=89.8」2014年の39才以下主婦のへそくり貯金額は65.0万円から89.8万円の間にあるといえます。」
所長:「OK」
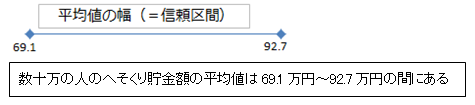
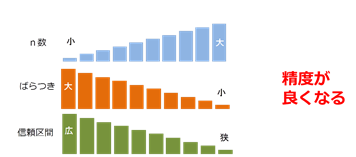
③ 信頼区間は幅が狭いほど推定の精度は良い
所長:「標本誤差(SE)が小さければ信頼区間はどうなると思う?」
雪乃:「区間の幅が狭くなります。」
所長:「区間の幅が狭いほど平均推定の精度が良いといえるんだ。」
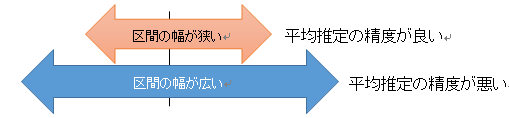
所長:「Aの信頼区間は69万円から91万円、Bは31万円から131万円だったとする。
どちらの方が平均値の推定は精度が良いかな。」
雪乃:「Aです。」
所長:「そうだね。Bの結果だと幅が広すぎて、へそくり貯金の推計は使いものにならないと思うよ。」
④ ヒゲとは何だろう
所長:「右の図を見てください。棒グラフの上部からT字型の棒が出ているよね。
これを『ヒゲ(error bar)』と言うんだ。ヒゲは何を表しているかな?」
雪乃:「40才以上主婦の2014年のへそくり貯金額の80.9±11.8万円でいえば、11.8万円の値がヒゲです。」
所長:「その通り。標本誤差11.8万円をグラフの上に乗せて描いたときの線をヒゲという。また、この標本誤差の半分を標準誤差(SE,Standard Error)といい、標準誤差をヒゲとする描き方もある。今回のグラフは標本誤差を使っているよ。」
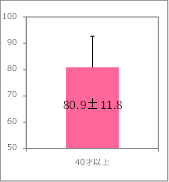
雪乃:「ヒゲは平均値グラフの上だけでなく下にも描くと、推定される平均値の幅がわかりやすくなると思うのですが、どうして描いていないのですか?」
所長:「それは棒グラフの中に納まって見にくいからだ。ただ、グラフによってはヒゲの下の部分も描いている場合もある。」
⑤「信頼区間」は○±△を図式化した以上の意味をもつ!
所長:「信頼区間は単に○±△を図式化したという以上の意味を持ちます。」
雪乃:「どのようなことですか?」
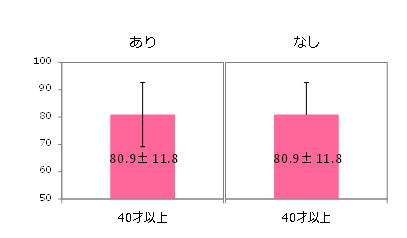
所長:「2014年における40才以上主婦と39才以下主婦のへそくり貯金額の信頼区間を並べてみてください。」
雪乃:「40才以上主婦 69.1万円~92.7万円」「39才以下主婦 65.0万円~89.8万円」
所長:「これらを並べた図にしてください。」
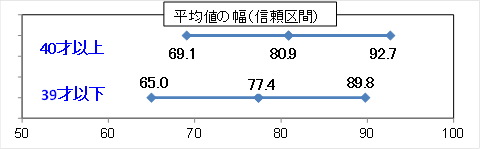
所長:「40才以上の平均値が最も低くなるのはいくつ?」
雪乃:「69.1万円です。」
所長:「39才以下の平均値が最も高くなるのはいくつ?」
雪乃:「89.8万円です。」
所長:「この結果からどのようなことが言える?」
雪乃:「そうですね、アンケート調査の結果は40才以上が80.9万円で39才の77.4万円より高くなっているのに、母集団における平均値は『40才以上が39才以下を下回る』ということがあるということですね。」
所長:「そうだ。グラフを見ると、40才以上と39才以下で平均値の幅が重なっているところがあるだろう。このような場合、『母集団における40才以上と39才以下の平均値に違いがある』とは言えないんだ。次の場合、母集団の平均値に違いがあるといえますか?」
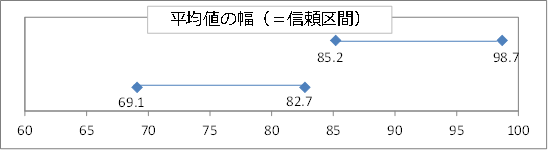
雪乃:「平均値の幅が重なっていないので、違いがあると言えます。」
所長:「その通り。」
雪乃:「図(上記)から母集団の平均値に違いがあることはわかりましたが、この結論は100%正しいといえるのですか?」
所長:「統計学は神様じゃないさ。外れることもあるよ。統計学から導かれる結論は当たる確率は95%、誤る確率は5%以下で信頼区間は求められている。」
⑥ 標本誤差は主婦数とデータのバラツキから求められる
所長:「データのバラツキを求める基本統計量は何?」
雪乃:「馬鹿にしないください。そのくらい知っています。標準偏差です。」
所長:「雪乃の友人から入手したデータ表をみせてください。このデータ表の末尾に標準偏差は記載されているね。
標本誤差は調査したデータの数(n)とデータのバラツキ(標準偏差 SD, Standard Deviation)から決まります。
nが大きいほど、バラツキが小さいほど標本誤差は小さくなります。」
雪乃:「とういことは、n数が大きくデータのバラツキが小さいほど、信頼区間の幅は狭くなり、精度が良くなるということですか?」
所長:「その通り。」
所長:「具体的には標本誤差の計算式は下のようになります。」

所長:「この式は覚える必要がないけど、この式の意味は理解しておくこと。」
雪乃:「分子に標準偏差、分母にn数か。ということは、データのばらつき度合いが小さく、n数が大きいと、標本誤差は小さくなりますね。標本誤差が小さいということは、信頼区間の幅は狭くなり、精度が良いということですね!」
所長:「その通り、下記表で標本誤差が最も小さいのは?」
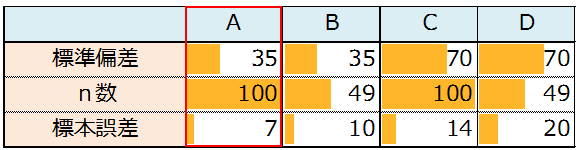
雪乃:「Aです。」
⑦ 母集団の平均値の違いを測るツール、それがp値
所長:「実は、母集団の平均値に違いがある、もしくは違いがあるとはいえない、というのは『p値(Probability Value)』というものを用いてもわかる。というよりは、最近はP値で違いを表現することが主流です。p値は標準偏差などと同様に手計算すると手間がかかるけど、今はパソコンのソフトウエアで瞬時に出力できるんだ。」
雪乃:「せっかく平均値の幅(=信頼区間)や、母集団の平均値に違いがあるかどうかを勉強したのに、無駄だったんですか?」
所長:「少しも無駄ではないよ。p値は、2つの信頼区間の重なり具合によって決まる値なので、信頼区間とp値は同じものだよ。」
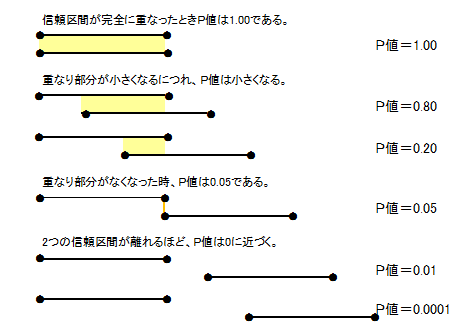
雪乃:「よく分かりました。」
所長:「p値が0.05より小さければ、信頼区間が重なっていないので、母集団の平均値に違いがあると判断する。
統計学では、p値<0.05の場合「有意差がある」という。p値が0.05より大きければ、信頼区間が重なっているので、母集団の平均値に違いがあるといえない(有意差がない)と判断する。」
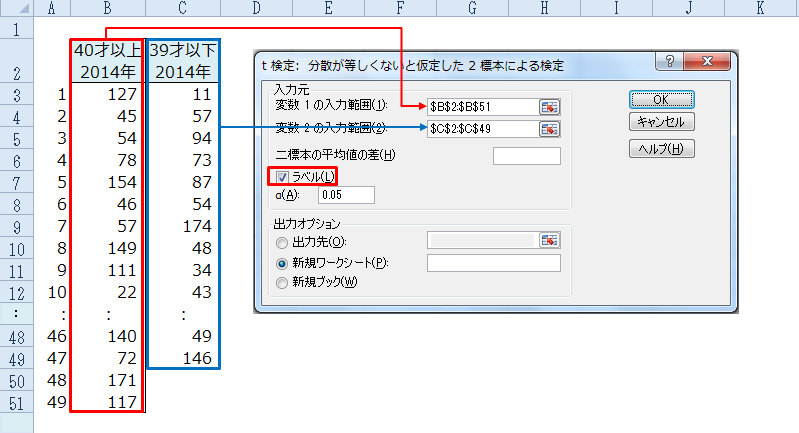
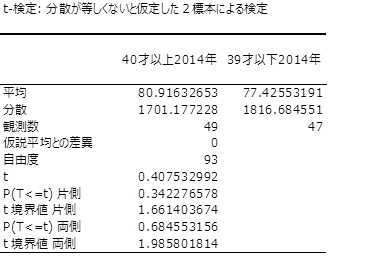
雪乃:「2014年における40才以上と39才以下の信頼区間のp値を教えてください。」
所長はExcelを起動させあっという間にp値を算出した。
所長:「p値は0.68です。これより40才以上と39才以下では有意差がないと判断する。」
雪乃:「p値が理解できてうれしいです。」
所長:「そんなに喜ばれたんだから、もう一つ付け加えよう。
p値はよく、体をかがめてバーをくぐるリンボーダンスに例えられる。かがんだ高さがp値で、バーの高さが0.05なんだ。
ということで、リンボーダンスのダンサー(求められたp値)がバー(0.05)を下回ればセーフで、母集団の平均値に違いがある(有意差がある)、と判断するのだ。」
雪乃:「リンボーダンス知らないので、かえってわからないです。」
所長:「そうなの、それは残念。」

雪乃:「質問です。有意差は「p<0.05」でなく「p≦0.05」と定義している場合もありますが、どちらの表記が正しいですか?」
所長:「“≦”か“<”にあまりこだわる必要はない。」
雪乃:「p値はどのようにして求めるのですか?」
所長:「計算式が複雑なため手計算ではできません。ソフトウエアを使って求めます。後でExcelの分析ツールでの求め方を紹介しよう。」
雪乃:「p値の0.05や0.016というのは、どういう意味なのでしょう?」
所長:「p値が0.016ということは、母集団の平均値に違いがあるという結論がもしかしたら0.016、すなわち1.6%の確率で誤りになるということ。」
雪乃:「ということは、p値が0.05だと5%の確率で誤りになるということですね。言い換えれば当たる確率は95%…、前回教えていただいた統計学の当たる確率95%と同じ数字ですね。」
所長:「その通り!Pは「Probability」(=確率)の頭文字です。」
⑧ 『対応のある』、『対応のない』とは何だろう
所長:「『対応のある』とか『対応のない』とかを知っているかな?」
雪乃:「聞いたことはあるけど意味は分かりません。」
所長:「『『対応のある』というのは、今回のケースでいえば、40才以上主婦49人のへそくり貯金額の2013年と2014年の比較のことだ。要は、同じ人についての比較すること。」
雪乃:「では、『対応のない』というのは何でしょう?」
所長:「『対応のない』というのは、今回のケースでは、40才以上主婦の2014年へそくり貯金額と39才以下主婦の2014年へそくり貯金額を比較すること。異なる主婦群について比較することだよ。次を見るとよく分かるよ。」
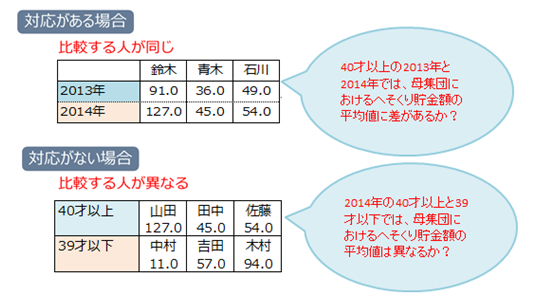
雪乃:「先にある調査概要の調査目的①を解決するには『対応がある場合』、②を解決するには『対応がない場合』を適用するということですね。」
所長:「その通り。『対応のある場合』と『対応のない場合』では、計算の仕方が違うよ。今からその違いを説明しよう。」
雪乃:「何か難しそう。易しく教えてくださいね。」
⑨ 対応のない場合の有意差判定
所長:「『対応のない場合』から説明しよう。
集団の平均値に着目して、母集団を調べることになる。今回のケースでいえば、40才以上主婦の2014年と39才以下主婦の2014年の平均値の違いを調べて、母集団の平均値の違いを評価することだ。」
雪乃:「先ほど、2014年において40才以上主婦と39才以下主婦の平均値は、それぞれの平均値の幅(=信頼区間)を算出して比較すると教えてもらいましたけど、その方法ではいけないのですか。」
所長:「その方法だよ。今までは『対応のない場合』を学んでいたんだ。
だから『対応のない場合』の説明はこれでおしまいにするが、今まで学んだことをまとめたまえ。」

⑩ 対応のある場合の有意差判定
所長:「今から『対応のある場合』の説明をするよ。」
雪乃:「よろしくお願いします。」
所長:「『対応のある場合』は、その集団の平均値に着目しないんだ。
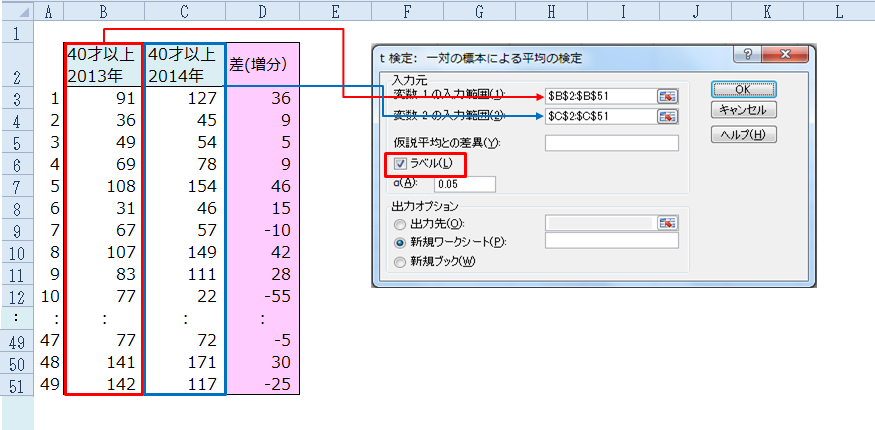
今回のケースでいえば、40才以上(もしくは39才以下)の2013年の平均値と、2014年の平均値を比較してはいけないということ。右の表は雪乃の友人が持ってきた40才以上主婦のデータだ。差(増分)は、へそくり貯金額について2014年~2013年を引いた値だよ。」
所長:「『対応のある場合』では個々の人の差に着目するのが特色だ。
主婦No1の差データはいくつかな?」
雪乃:「36.0万円です。」
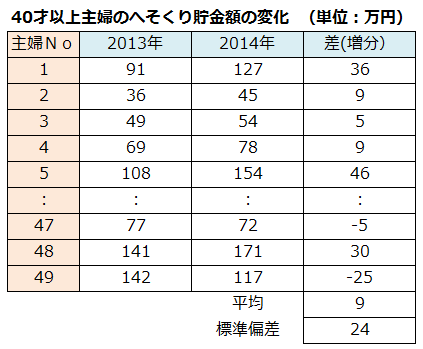
所長:「『差データ』の49人分の平均値を計算してください。」
雪乃:「36.0+9.0+5.0+……(-5.0)+30.5+(-24.4))÷49=9.2万円です。」
所長:「次に、この『差データ』の信頼区間を計算してみよう。信頼区間を求めるには、まずは何を計算するのかな。」
雪乃:「標本誤差です。」
所長:「標本誤差の計算方法を覚えなくてもよいといったけど。ここでもう一度だけ使ってみよう。」
雪乃:「計算してみます。標本誤差の公式を使います。」
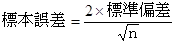
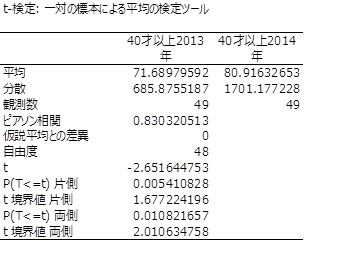
雪乃:「田中君の持参データの末尾に記載されている『差データ』の標準偏差は24.4万円です。
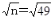
=7 標本誤差は2×24.4÷7=7.0 です。信頼区間は平均±標本誤差 なので、『差データ』の信頼区間は9.2±7.0
これより2.2万円 ~ 16.2万円になります。」
所長:「よくできました。
『対応のある』データの場合、この『差データ』の平均値の幅(信頼区間)が-(マイナス)の値から+(プラス)の値の間にあるのかどうか、この例題のように+(プラス)の値から+(プラス)の値の間にあるのか、すなわち信頼区間の間に0(ゼロ)を挟むかどうかが、重要なのだ。0(ゼロ)を挟むということは+(プラス)も-(マイナス)もあるということだよ。
+(プラス)の場合は2014年が高くなり、-(マイナス)の場合は2013年が高くなる。」
雪乃:「よく分かりません。」
所長:「40才以上主婦の2013年と2014年の『差データ』の平均値の幅は2.2万円 ~ 16.2万円で0(ゼロ)を挟まない。
ということは、別の40才以上主婦でも『差データ』の平均値はこの幅の範囲内となり、すなわち40才以上は39才以下を上回り、へそくり貯金額の増加が認められることになる。すなわち、母集団の2013年と2014年の平均値に違いがある、といえる。」

所長: 「一方で、『差データ』の平均値の幅に0(ゼロ)を挟んでいる場合は、別の主婦を調べたら『差データ』の平均値が+(プラス)になることも、-(マイナス)になることも、0(ゼロ)になることもある。ということは、39才以下主婦の2013年と2014年でへそくり貯金額の増加が認められたり、認められなかったり、変わらなかったりするということであり、2013年と2014年で平均値に違いがあるかわからないということになる。すなわち、『母集団の平均値に違いがある、とは言えない』と判断する。」
雪乃:「やっと分かりました。」
所長:「39才以下主婦の2013年と2014年の『差データ』の平均値の幅(信頼区間)を計算してください。」
雪乃:「公式を使います。」
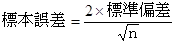
「田中君の持参データの末尾に記載されている『差データ』の平均値は10.6万円、標準偏差は36.5万円です。」
√n=√47=6.86 「標本誤差は2×36.5÷6.86=10.7 です。
信頼区間は平均±標本誤差 なので、『差データ』の信頼区間は10.6±10.7
これより -0.1万円 ~ 21.3万円になります。」
所長:「グラフを描いてみて。」
雪乃:「了解です。」

所長:「39才以下主婦の2013年と2014年では、母集団におけるへそくり貯金額の平均値に違いがありますか?」
雪乃:「ありません。」
所長:「『対応のある』場合でp値を求めてみると次になるんだ。」
雪乃:「分かりました。」
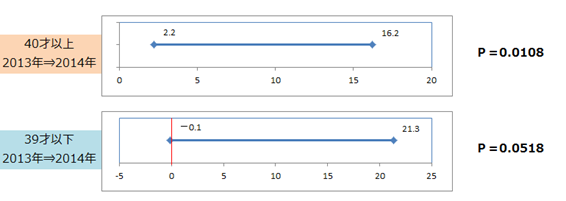
所長:「ちなみに40才以上と39才以下の2013年⇒2014年のp値は次のとおりです。」
調査報告
雪乃の田中君への回答
この回答を持って、後日、田中君と会った雪乃。
「2013年⇒2014年のへそくり貯金額の増加について、39才以下主婦の方が増分が大きいのに、有意差は39才以下主婦で「ない」、40才以上主婦で「ある」という結果になっているのはなぜか。」との疑問に対して、次の回答をしました。
40才以上の差データ、39才以下の差データの平均値を見ると、39才以下の増分が大きいです。しかし、40才以上の49人、39才以下の47人それぞれのデータのバラツキに着目すると、39才以下の方がデータのばらつき(標準偏差)が大きいです。
差データの標準偏差 40才以上→24.4 39才以下→36.5
統計学上の処理を行うと、40才以上のp値は0.0108、39才以下のp値は0.0518でした。
p値は平均値だけでなく、n数やデータのバラツキも考慮して算出されます。
今回のデータでは、n数は両群間に大きな差がないことから、このp値の差はデータのバラツキに起因すると考えられます。また、p値は一般的に0.05を下回れば「有意差あり」、上回れば「有意差なし」と判断しますので、39才以下主婦はわずかですが、統計学上では『有意差なし』となります。
田中:「雪乃さん、すばらしい。ところで、40才以上より、39才以下で標準偏差が大きいということはどういう事なの。」
雪乃:「それはですね。えーと、田中君の持参したデータを見て説明するね。各々最も小さい値と最も大きい値を探してみて。」
田中:「40才以上➡最小値:-55 最大値:54」「39才以下➡最小値:-75 最大値:85」
雪乃:「39才以下主婦の方が2013年→2014年の変動が大きいということ。差データの平均値の推定は変動が大きい方がしにくい。だから有意差がある判定がしにくくなると思ってくれればいいわ。」
田中:「説明もうまいなー。これから時間ある?ご馳走するよ。」
第5話 終わり
制作: 菅 民郎
理学博士
株式会社アイスタット代表
ビジジネス・ブレークスルー大学大学院 名誉教授
参考 Excelの分析ツールを使って有意差を調べる
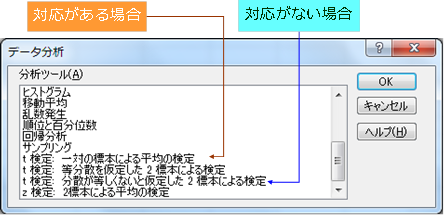
対応がある場合
対応がない場合