3.2 変動変数 ~100m走と縄跳びで個人差の大きいのはどちらか~
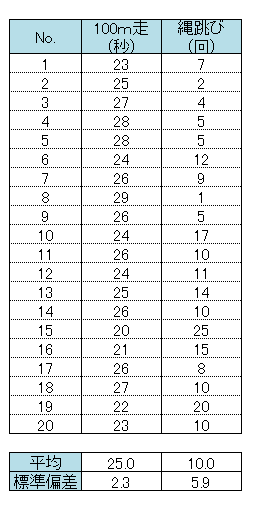
体力測定の記録
ダイスケは小学校6年生の担任をしています。
普段の体育の授業を見ていると、男子生徒は基礎体力の個人差が大きいように思えます。
そこで100m走と二重跳び(縄跳び)のテストを行い、個人差が大きい種目を重点的に指導しようと考えました。
ダイスケは、それぞれの種目の標準偏差を計算して、値が大きい方を個人差が大きい種目と判断すればよいと考えました。
しかし標準偏差の使い方に自信がないので莉子さんに聞いてみることにしました。
(莉子)確か、標準偏差は単位が同じでなければ
比較をしてはいけないはずよ。
(ダイスケ)そうなの!?じゃあ、どうすればいい?
私には比較してはいけないことしかわからないわ。
その先は先生に聞いてみましょう。
単位が違うデータの比較
(先生)よく覚えていたね。
標準偏差は単位が異なる場合は比較をしてはいけないよ。
今回は単位が「秒」と「回」で違います。どうすればいいですか。
単位が違うデータのバラツキを比較するには、標準偏差ではなく
変動係数を用いるんだ。
標準偏差と同じようにバラツキが大きいほど値が大きくなる。
変動係数の求め方を知りたいけど難しいかしら・・・。
標準偏差が分かっていれば難しいことはないよ。
変動係数は標準偏差を平均で割った値だからね。
まずは簡単な例題で説明しよう。
変動係数の例
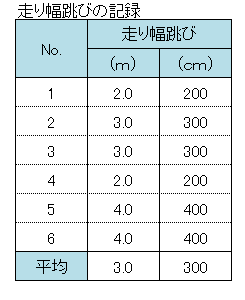
右記のデータは小学6年生6名の走り幅跳びの結果です。
単位を変えただけで、結果は全く同じものです。
まずはバラツキを見るために、標準偏差を求めてみましょう。
標準偏差の計算方法を思い出してください。
- ひとりひとりのデータから平均値を引きます。(=偏差)
- 求めた偏差を2乗します。(=偏差平方)
- すべての偏差平方を合計します。(=偏差平方和)
- 偏差平方和をデータ数で割ります(=分散)
- 分散の平方根(ルート)を求めます。(=標準偏差)
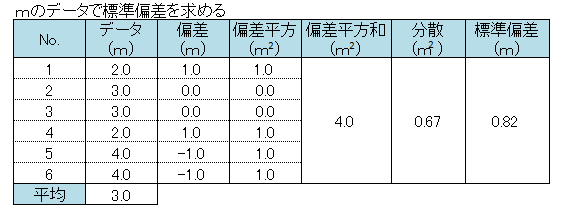
まずは単位が「m(メートル)」のデータについて計算してみましょう。
標準偏差の計算過程は上記のようになります。
求められた標準偏差82を平均300で割ります。
0.82 ÷ 300 = 0.27
この値が変動係数です。
同じように単位が「cm(センチメートル)」のデータについても計算してみましょう。
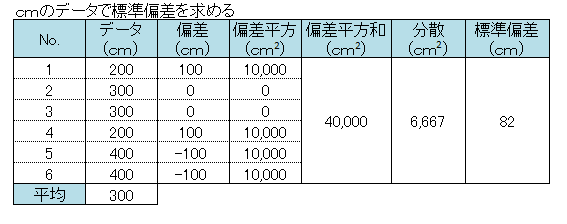
標準偏差は異なりますが、変動係数はどちらも同じ値になりました。
変動係数を用いれば、単位が異なっても比較が可能であることがわかりました。

