3.1 相関係数 ~暑い日のアイスクリームの売れ行きと、店長の機嫌の関係は?~
暑いと人は怒りっぽくなるか
大学生のユキは、夏休みにコンビニでバイトをしています。
暑い日にアイスクリームの売上が増えるのはわかるのですが、店長が怒る回数も増えているような気がします。
暑さと店長の怒る回数に関係はあるのか、単にその日の気まぐれなのか、知りたくなりました。
ユキは高校時代の家庭教師である莉子に相談してみました。
(莉子)ユキちゃん、夏休みのバイトはあと何日ぐらいあるの?
(ユキ)20日ぐらいかしら。
バイトに行った日の最高気温と店長がその日に怒った回数を調べられる?できればアイスクリームの売れた個数も調べておいてね。
データが集まったら、先生のところへ一緒に行ってみようよ。
関連性を調べる
莉子とユキは、データを持って先生のところへ相談に行きました。
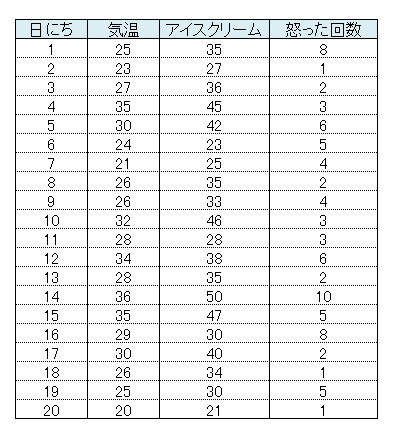
(先生)データをちゃんと持ってくるとは、さすがだね。
データがあれば話が早い。早速、考えてみよう。
ユキちゃん、散布図を描いてみて。
散布図って何ですか?
原因となる項目が横軸、結果になる項目が縦軸になるように書いた点グラフよ。気温とアイスクリーム売上個数のどちらが原因で、どちらが結果か考えてみて。
つまり暑いからアイスクリームが売れるのか
アイスクリームが売れるから暑いのかどちらだと思う?
もちろん、暑いからアイスクリームが売れるんです。
う。つまり原因が気温、結果が売上個数ってことね。
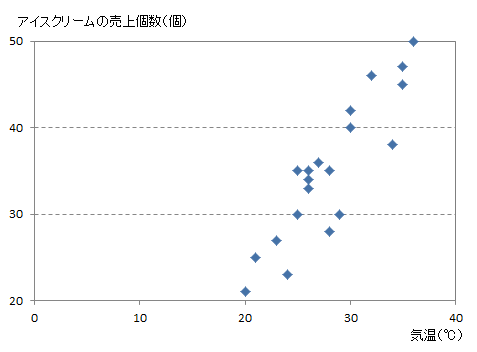
横軸に気温、縦軸にアイスクリーム売上個数をとってグラフを書いてみます。
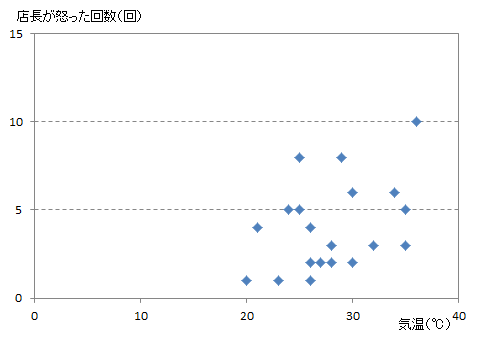
私は気温と店長が怒った回数を描いてみよう
散布図を描くと両者の関係がなんとなく見えてくるんだ。
気温が高いほどアイスクリームがよく売れているようだね。
でも気温が高いからといって店長がよく怒るとは言えなさそうだ。
ところで、アイスクリームのグラフは、点が直線状に並んでいるのがわかるかな?
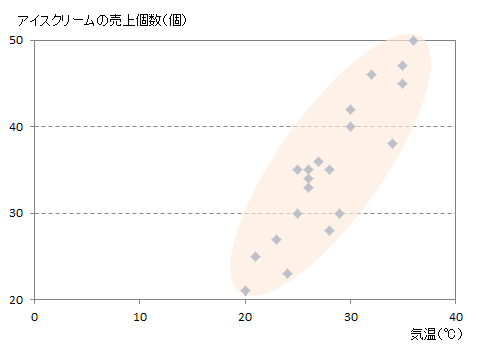
ええ。直線に近い形にまとまっているわ。
直線的傾向があると、両者に関係があると言えるんだ。怒った回数の方は、点がだんご状態で直線的傾向があるとは言えない。
つまり暑いから店長がよく怒ったとは言えないんだ。きっとユキちゃんたちが暑い日に、たまたま怒られるようなことをしたんだね。
そうかもしれないわ。
この関連性を散布図じゃなくて具体的な数値で表すことはできますか。
相関係数を使えば、0から1の間の数値であらわすことができるよ。
関連性が強いほど、散布図で言えば直線的傾向が強いほど、相関係数は1に近い値になるんだ。
相関係数が0.5より大きいときには両者に関連性があると判断することができる。
計算してないからわからないけど、おそらくアイスクリームの売上個数と気温の相関係数は1に近く、店長の怒った回数との相関係数は0.5を下回っていると思うよ。
すごい!どうやって計算すればいいですか。
相関係数を求めるには、まず共分散について知っておく必要があるんだ。なぜなら共分散をそれぞれの標準偏差で割った値が相関係数だからだよ。
まずは共分散、そのあとに相関係数を説明しよう。

