相関係数の求め方
原因となる項目(気温)をX、結果となる項目(売上個数)をYとします。
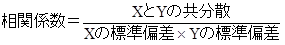
- Xの標準偏差を求めます。
- Yの標準偏差を求めます。
- XとYの共分散を求めます。
- Xの偏差とYの偏差を掛けます。(=偏差の積)
- 偏差の積を合計します。(=偏差の積和)
- データの数で割ります。(=共分散)
- 公式に標準偏差と共分散をあてはめて相関係数を求めます。
アイスクリームの売上と店長の機嫌の相
20日分のデータの分析結果は下記のようになりました。

アイスクリームの売上個数と気温との相関係数は0.89、店長の怒った回数との相関係数は0.41で、先生の予測通りになりました。
ありがとうございました。
ちょっと待って。相関係数についてもう少し説明が必要だ。
相関係数は、正確には-1から1の間の値をとる。
-1または1(つまり|1|)に近いほど相関関係は強く、0に近いほど弱くなる。
※|X|のXの絶対値。数値の大きさを表すので必ずプラスの値となります。-1も1も絶対値は1です。
相関係数にはマイナスもあるんですか。
気温が上がるほどアイスクリームの売上も上がったよね。このような時、両者に正の相関があると言うんだ。相関係数はプラスになる。これとは逆に気温が上がるほど売上が下がる場合がある。
例えばおでんや焼芋などが該当するだろう。このような時、両者には負の相関があると言うんだ。相関係数はマイナスになる。グラフのイメージとしてはこんな感じだ。
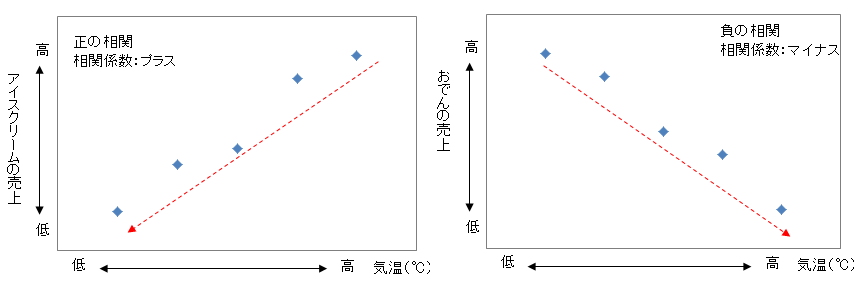
- 正の相関:Xの値が大きくなるにつれてYの値も大きくなる、右上がりの直線的な関係。
- 無相関:XとYの間に直線的な関係は見られない。
- 負の相関:Xの値が大きくなるにつれてYの値は小さくなる、右上がりの直線的な関係。
相関係数がいくつだったら強い関係があると言っていいですか?
残念ながら相関係数がいくつ以上であれば強い、いくつ以下であれば弱い、と言った明確な基準はないんだよ。分析する人が経験から決まるしかないよね。
初めに言ったように、僕は0.5を基準に相関がある、ないを判断している。参考までに、僕の基準を教えよう。
相関係数を r とすると、

Excelによる相関係数の計算
共分散、相関係数はExcel関数を使えば簡単に求めることができます。
意味を理解できたら、あとはExcelを使って計算しましょう。
共分散: =COVAR(Xのデータ範囲、Yのデータ範囲)
相関係数:=CORREL(Xのデータ範囲、Yのデータ範囲)
共分散: =COVAR(Xのデータ範囲)
ワンポイント
相関係数とは
相関係数はXとYに直線的な関係があるかどうかをみるための指標であって、曲線や円などの傾向を見るものではありません。
右のグラフを見てみましょう。左図は山型、右図は円型で、XとYに何らの関係があることが予想されます。
しかし直線的な関係ではないため相関係数はどちらも0に近い値になっています。

相関の程度
相関係数が0でない限り、弱いながらも相関はあると言えますが、その程度が強いかどうかを調べることに意味があります。
無相関の検定
ユキがバイトしているコンビニでは、アイスクリームの売上と気温の相関係数は0.89で強い相関があることがわかりました。しかしすべての店舗について同じことが言えるかどうかはわかりません。
すべての店舗について調べるのは大変ですが、一部の店舗について調べることで、すべての店舗について強い相関(0.7以上)あるかどうかを知ることができます。
これを相関検定といいます。 また、強い相関とは言わないまでも、ゼロでない相関があるかどうかを調べる方法を無相関の検定といいます。

