2.1 平均値と中央値 ~わんこそば大会の勝者は?~
平均の落とし穴
大学生のひとみはゼミの旅行で盛岡に行きました。
盛岡と言えばわんこ蕎麦。早速みんなでチャレンジすることにしました。
すると教授から女子対男子の対抗戦の提案があり、勝った方に商品を出してくれることになりました。
ハンディがないので一見不公平のようですが、女子には頼りになる まる子 がいるので大丈夫。
結果は予想通り。
まる子が163杯食べたおかげで女子の勝ちです。
ところが男子からブーイングが・・・。
まる子を除けば男子全員が、女子に勝っているというのです。

確かに・・・。男子は一番少ない人でも34杯。女子はまる子以外、全員34杯以下です。
(ひとみ)でも仕方ないわ。平均でみれば女子の方が多いんだから。
ひとみは愛嬌を振りまいて何とか男子を説得しましたが、後味が悪く、帰ったら莉子先輩に判断が正しかったかどうかを相談に行くことにしました。
(莉子)そうねぇ。平均が高いから女子の勝ちでいいと思うわ。
でも男子からしてみたら納得がいかないこともわからないでもないわ。
先生に聞きに行きましょう。
平均値と中央値の仕組み
(先生)すごい子がいるね。
163杯も食べられたら大会で優勝できそうだね。
それより女子の勝ちって決めたことは間違ってないですよね。
その前に、平均値について改めて考えてみよう。
たくさんあるデータを1つの数字で表現した値を代表値と言うんだ。
平均値は代表値のひとつだよ。
でもたった1つの値ですべてを表現するのはときに無理が生じる。
今回のように飛びぬけて大きな値(または小さい値)があるときもそうだ。このような値がある場合、平均値ではなく中央値を使うといいよ。
中央値も平均値と同じく代表値のひとつで、名前の通りちょうど真ん中にくる値だ。
まる子は確かに飛びぬけているわね。
そう。他の19人とは違うね。
中央値の計算方法を教えてください。
中央値は計算ではないけど、求め方を簡単な例で説明しよう。
平均値と中央値の例
次のデータは、小学生5人のお年玉の金額です。
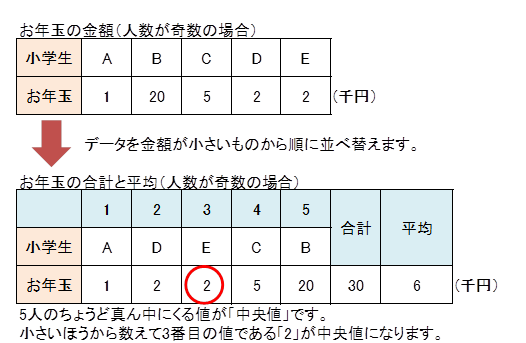
平均値は6千円。中央値は2千円。ずいぶん違うわ。
中央値を使うと、外れ値(他の多くの値と極端に離れている値)の影響を受けないんだ。
なるほど。でも人数が偶数だったら真ん中を決められないわ。
6人だったら3番目と4番目の人の平均をとればいい。
次の例で説明しよう。
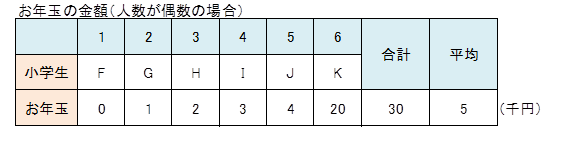
3番目が「2」、4番目が「3」だから2と3の平均が中央値だ。

