2.2 度数分布とヒストグラム ~新入り英太郎の作る金太郎飴はバラバラか~
バラバラの飴
莉子がよく行くお菓子屋さんでは、金太郎飴の実演販売をしています。
お徳用袋の100個入り300gが売れ筋ですが、お客さんから「新入りの英太郎が作ると店長が作るときよりも飴が小さいぞ」とクレームがきました。
お徳用袋は英太郎が作ってもちゃんと100個入り300gに仕上がっています。
店長は困ってお得意さんの莉子に相談しました。
(店長)ちゃんと300g入りなのにクレームが来たんだよ。お客さんを納得させる説明をしたいんだけど・・・。
飴のバラツキ
莉子は早速、先生のところへ相談に行きました。
(莉子)容量も平均も同じなのに小さい飴が多いってことはあるんですか?
(先生)まず袋を開いてひとつひとつの重さをチェックしてごらん。
莉子は地道に飴の重さを量って先生に報告に行きました。
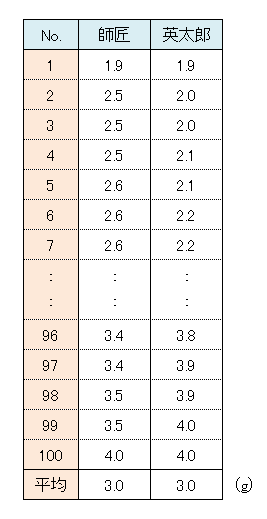
飴100個の重さを量って昇順に並べてみました。
重さはどちらもいちばん小さいもので1.9g、大きいもので4.0gと一緒でした。
やっぱりお客さんの思い過ごしでしょうか。
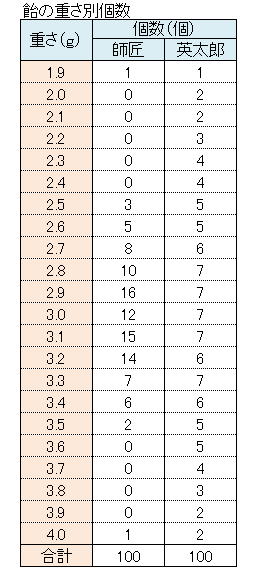
データを見ていてもわからないから、重さごとに飴の数を数えてごらん。2.0gの飴が何個、3.0g飴が何個・・・というようにね。
そうやってまとめた表をもとにグラフを書いてみると何かが見えてくるかもしれないよ。
重さごとに飴の数を数えて一覧表にしました。これからどんなグラフを書けばいいのかしら。イメージがわかないわ。
それでは、とりあえず簡単な例で練習してみよう。
ヒストグラムを作ってみる
次のデータを見てください。これは学生10人のテスト結果です。
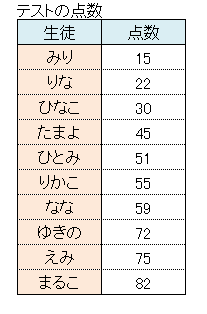
点数ごとに人数にかえてみましょう。
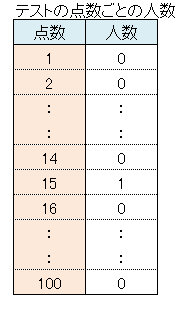
点区切りで数えると、行のデータになってしまって大変です。ある程度、点数をまとめましょう。

20点、21点・・・と等しい間隔で区切りました。この区間を階級と呼びます。そして、それぞれの階級に該当する人数を度数といいます。

各階級に属する生徒の、全生徒10人に対する割合を計算しましょう。割合のことを統計学では相対度数といいます。一般的には割合%(例:45%、70%)、相対度数は小数点(例:0.45、0.70)で表示します。
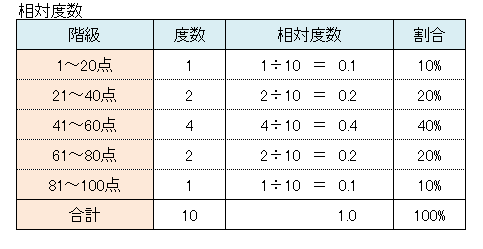

階級と相対度数(または度数)のデータを用いて棒グラフを作成します。このとき、棒の間隔はあけないのが一般的です。
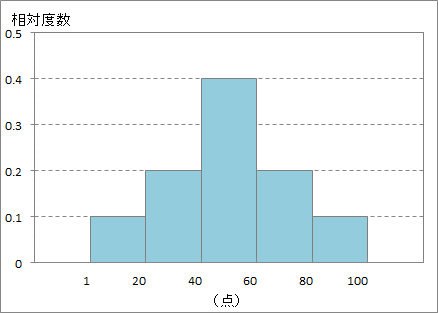
この棒グラフはヒストグラムと呼ばれています。
階級の決め方によって、データの特徴をとらえやすくなったり、そうでなくなったりするよ。
階級の幅はどうやって決めればいいのですか?
それは分析する人が判断することで、決まりはないよ。
階級の幅を変えて、ヒストグラムをいくつかつくってごらん。
その中から特徴をとらえやすいものを採用すればいい。

