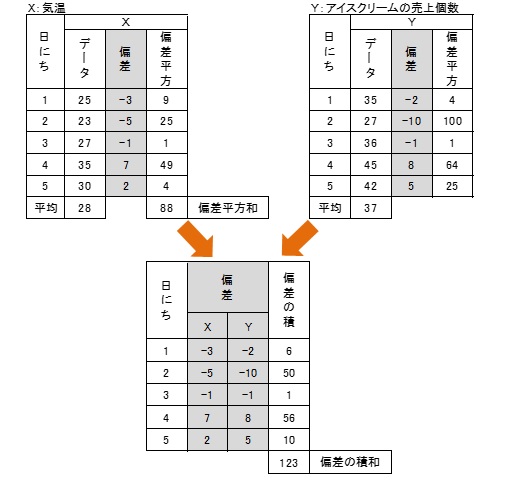
では、aとbを求めてみましょう。
b=偏差の積和 ÷ Xの偏差平方和
=123 ÷ 88=1.4
次にaです。
a=Yの平均値-b × Xの平均値=37-1.4 × 28=-2.1
aとbが求められたので回帰式が決まりました。
Y=-2.1+1.4X
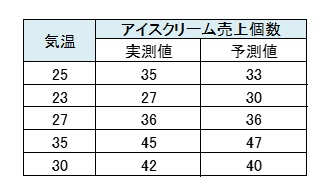
回帰式に気温Xを代入すれば、アイスクリームの売上個数Yが予測できます。
実測値と予測値とを比較すると、ほぼ近い値となっているのでこの回帰式は予測に使えると判断します。
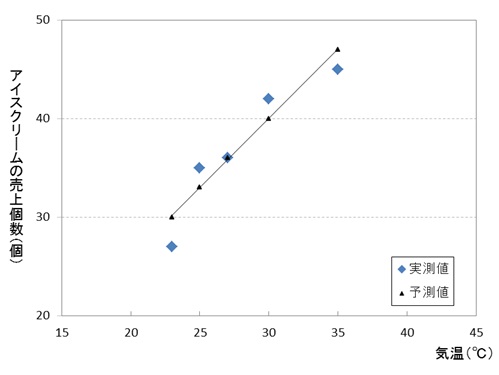
これらの予測値Yを直線で結ぶと回帰直線が描けます。

回帰式の求め方
- 2つのデータの相関係数を求めます。
- 相関が強いことが確認できたら回帰式を求めます。
- 求められた回帰式を用いて予測を行います。
②の求め方
- XとYの平均を求めます。
- Xの偏差平方和を求めます。
- Xについて、それぞれのデータから平均値を引きます。(=偏差)
- 求めた偏差を2乗します。(=偏差平方)
- すべての偏差平方を合計します。(=偏差平方和)
- XとYの偏差の積和を求めます。
- 「Xの偏差」と「Yの偏差」を掛けます。(=偏差の積)
- 「偏差の積」を合計します。(=偏差の積和)
- 公式にデータを代入します。
b=偏差の積和 ÷ X の偏差平方和
a=Yの平均値 - b × X の平均値
アイスの売上と気温の関係を回帰分析してみる
(先生)同じように20日分のデータの回帰分析を行ってごらん。
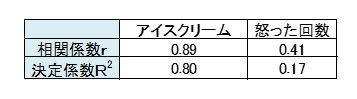
(莉子)相関係数は0.89で高いことは確認済みだから、早速回帰式に必要な値を計算してみました。
必要なデータ(右表参照)をまとめました。
データがそろったね。あとは直線の式に当てはまるだけだ。
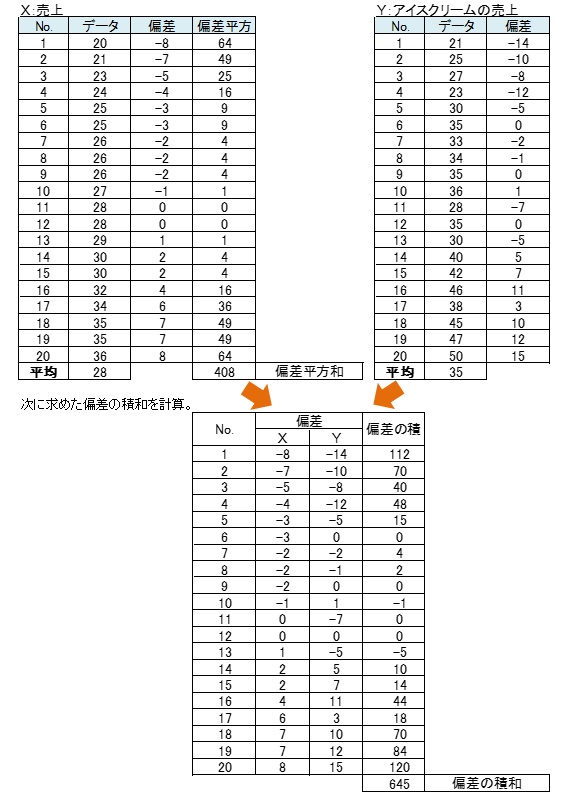
Y=a+bXだから、まずbを計算します。
b=偏差の積和 ÷ Xの偏差平方和=
645÷408=1.58
そう。bが求められたから次はaだね。
a=Y-bX=
35-1.58×28=-9.26
直線が求められました。
Y=-9.26+1.58X
です。
その通り。
散布図に直線 Y=-9.26+1.58X を加えるとこんな感じだ。
(下図参照)
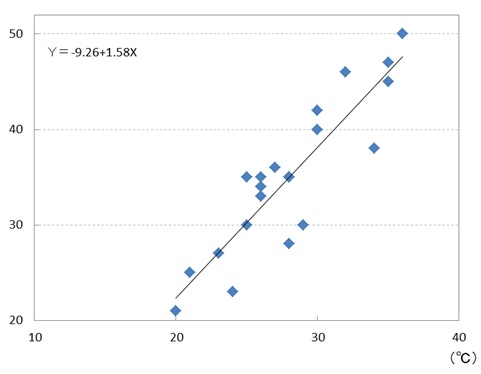
データの真ん中を通る線引けたわ。
この回帰式を用いれば、気温から売上個数が予測できるわけだ。
店長の怒った回数は求められないのかしら。
計算上は求められるよ。
でも今回、直線回帰分析を行ったのは相関が高かったからだ。
相関係数が低ければ、直線回帰分析を行っても求められる回帰式は使いものにならない。相関係数が0.7以上を目安にするといいよ。
そうだった。怒った回数と気温の関係の散布図は、直線の当てはまりが悪かったんだわ。
いわゆる「分析の精度が低い」ということだ。
分析の精度を表す指標として相関係数と同様によく使われる値に決定係数というものがある。
詳しい説明は省略するけど、実測値と予測値の相関係数を2乗したものと一致する値だ。どちらで判断してもいいよ。
散布図を描くと両者の関係がなんとなく見えてくるんだ。
Excelによる回帰分析
直線回帰式 Y=a+bX の a と b はExcel関数を使えば簡単に求めることができます。
傾き b=SLOPE(Yのデータ範囲,Xのデータ範囲)
定数項 a=INTERCEPT(Yのデータ範囲,Xのデータ範囲)
回帰分析は、Excelの分析ツールを使っても実行できます。
[分析ツール]→[回帰分析]

