3.2 直線回帰分析 ~天気予報から売り上げを予測する~
翌日の売上を、予測気温から予測する
(ユキ)アイスクリームと気温の関係が強いことはよく分かったけど、これを何に利用することができるの。
(莉子)関係が強いってことは気温が分かればアイスクリームの売上を予測することができるってことじゃないかしら。
気温から売上を予測するなら、週間天気予報を見ておけばいいわね。
売り切れなんてことがないように仕入れを調整できるわ。
莉子先輩、先生に予測の方法も聞いてもらえるかしら。
もちろんよ。
散布図に直線を引いてみる
相関係数が高いってことは、直線的な関係が強いってことだと言っていましたよね。
気温とアイスクリームの売上は相関係数が0.89と高いから、気温から売上を予測することができるんじゃないですか。
(先生)莉子さん、よく気がついたね。君の言うとおりだ。
散布図の点の真ん中を通るように直線を引いてみた。この直線の書き方と、直線の式がわかれば気温から売上個数を予測できるよ。
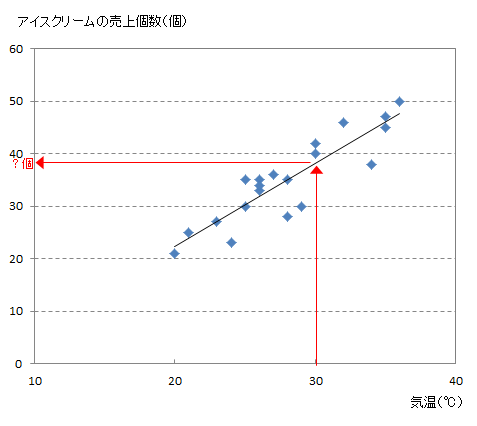
やっぱり!それでは、この直線の求め方を教えてください
この直線は回帰直線というんだ。直線の式はExcelで簡単に求めることができるけど、勉強のために考え方を説明しておこう。
回帰直線の求め方
まずは5日分のデータで考えてみましょう。
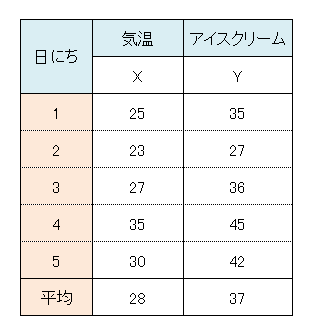
実際に直線を書いてみましょう。直線は気温(X)と売上個数(Y)の平均を必ず通ります。平均の点を固定し、すべての点からなるべく近くなるように直線を引くことを考えます。
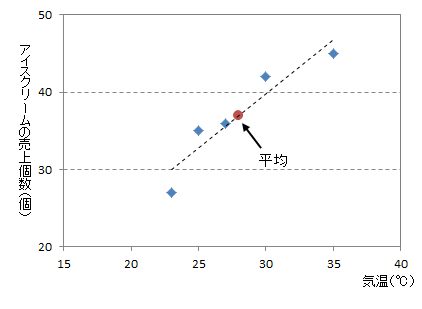
すべての点から最も近くなる直線とは、ある気温に対する実際の売上個数と、同じ気温に対する直線上の値の距離を考えます。
前者を実測値、後者を予測値と呼びます。すべてのXについて実測値と予測値の距離を求めて合計した値が、最も短くなるような直線がすべての点から最も近くなる直線です。
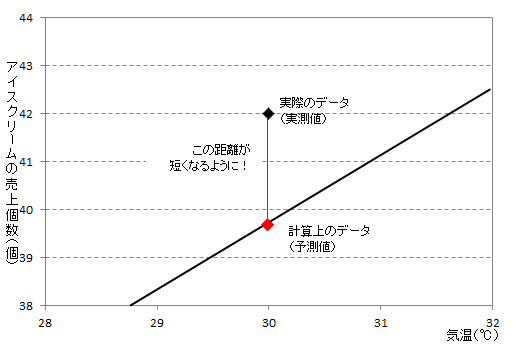
しかし、これはあくまで考え方です。実際には、この直線を求める公式が存在しますので、そちらを利用しましょう。このようにして引かれた直線を回帰直線といい、回帰直線の方程式を回帰式といいます。
直線回帰分析とは2つの項目の関係を一次式で表現する解析手法です。回帰分析は説明変数が1つ、目的変数が1つです。説明変数とは原因となる項目、この例では気温です。目的変数とは結果となる項目、つまり売上個数です。

