共分散構造分析 ≪2/6 ≫
パス図
パス図に適用する図形について説明します。
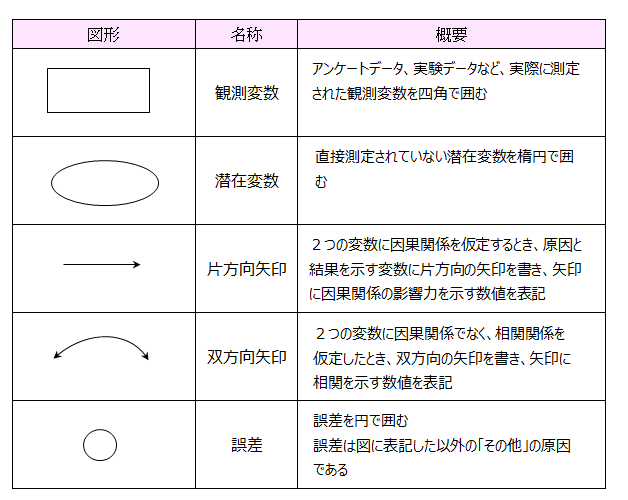
【パス図】
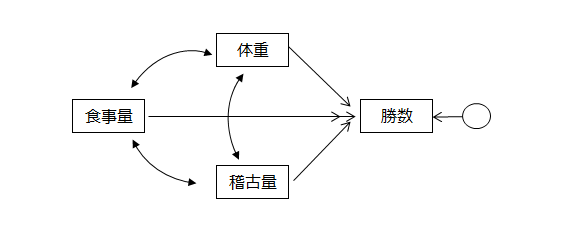
【例】
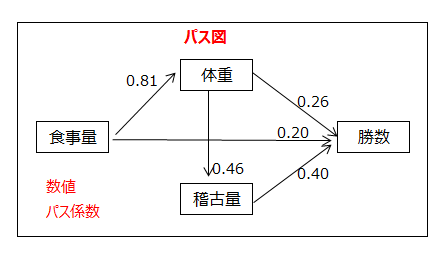
パス係数(標準化解/非標準化解)
パス係数は変数間の相関関係、因果関係を表す値です。パス係数には標準化解と非標準化解の2種類があります。
標準化解はすべての観測変数と潜在変数の分散を1に基準化して求めたときの値、非標準化解は基準化しないそのままのデータについて求めたときの値です。分かりやすい例として重回帰分析を取り上げると、回帰係数は非標準化解、標準回帰係数は標準化解です。
パス係数の強さを解明するときは標準化解、パス係数の大きさを解明するときは非標準化解を用います。
下記の上図のパス係数は例題1の標準化解、下図のパス係数は非標準化解です。
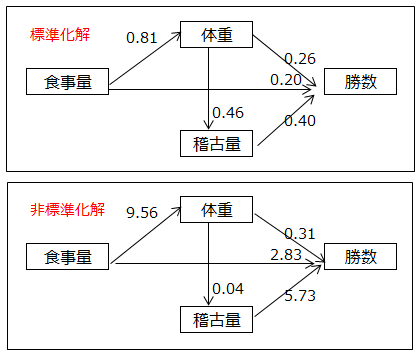
・標準化解の解釈
体重→勝数、食事量→勝数、稽古量→勝数のパス係数をみると、0.26、0.20、0.40です。
勝数への影響度が最も強いのは稽古量、次に体重、食事量が続きます。
・非標準化解の解釈
稽古量と食事量のデータは「多い」「普通」「少ない」の3段階です。稽古量が1段階増えると勝数は5.73勝増える、食事量が1段階増えると勝数は2.83勝増えることを意味しています。
体重から勝数への係数は0.31で、食事量が一定であるならば、体重が1kg増えると勝数は0.31勝増えることを示しています。
直接効果と間接効果(直接パス/間接パス)
食事量から勝数へのパスは2経路あります。
「食事量→勝数」の直接パスと、「食事量→体重→勝数」の体重を経由する間接パスです。
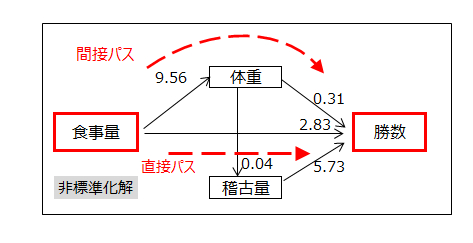
直接パスは、体重を経由しない、つまり、体重が一定であるとき、食事量が1段階増えたときの勝数は2.83勝増えることを意味しています。 これを直接効果といいます。
間接パスについてみてみます。
食事量から体重への係数は9.56で、食事量が1段階増えると体重は9.56kg増えることを示しています。
体重から勝数への係数は0.31で、食事量が一定であるならば、体重が1kg増えると勝数は0.31勝増えることを示しています。
食事量が1段階増加したときの体重を経由する勝数への効果は 9.56×0.31=2.96 と推定できます。
これを食事量から勝数への間接効果といいます。
この解析から、食事量から勝数への総合効果は、直接効果+間接効果=総合効果で計算できます。2.83+2.96=5.79
となります。
この式より、食事量の勝数への総合効果は、食事量を1段階増やすと、平均的に見て5.79勝、増えることが分かります。
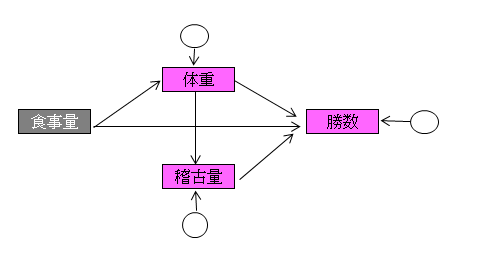
外生変数と内生変数
パス図のモデルの中で、どこからも影響を受けていない変数のことを外生変数といいます。 他の変数から一度でも影響を受けている変数のことを内生変数といいます。
下記パス図において、食事量は外生変数(灰色)、体重、稽古量、勝数は内生変数(ピンク色)です。
内生変数は矢印で結ばれた変数以外の影響も受けており、その要因を誤差変動として円で示します。 したがって、内生変数には必ず円(誤差変動)が付きますが、パス図を描くときは省略しても構いません。