目次
共分散構造分析の事例 ≪4/6 ≫
例題
≪例題3≫
大学受験進学塾で、有名校T大学に合格した13人と不合格の17人を対象に、アンケート調査を行いました。
塾生の家庭環境、学習方法、知的能力と合格有無との因果関係を明らかにしてください。
【質問文】

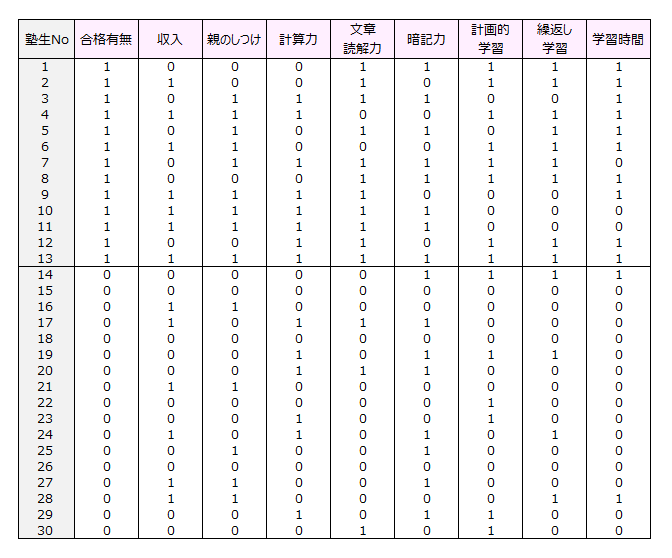
【回答データ】
共分散構造分析の解析手順
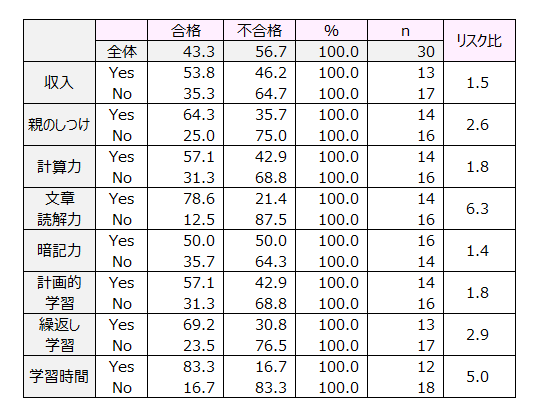
合格有無と相関分析
合格有無とその影響要因8項目とのクロス集計を行い、リスク比を算出しました。
リスク比は、影響要因ごとに合格割合YesをNoで割った値で、Yesの生徒はNoに比べ「何倍合格できる」と解釈できます。
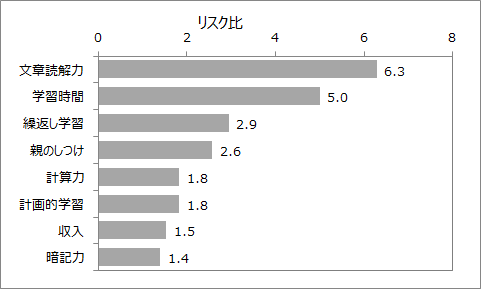
リスク比の降順で並べました。
合格有無に影響度が最も高いのは、文章読解力で次に学習時間、繰り返し学習が続きます。
影響要因相互の相関分析
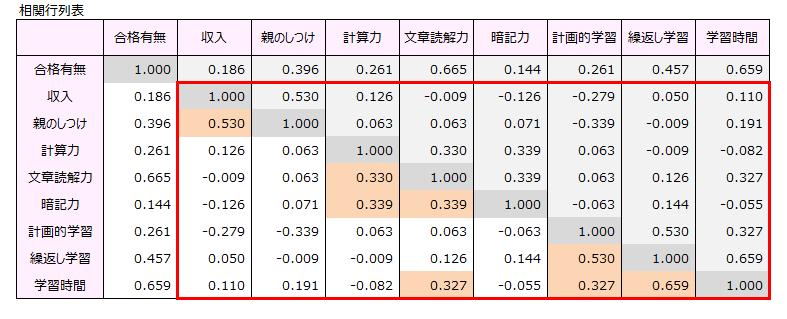
質問9項目相互の単相関係数を算出しました。
影響要因相互の相関(赤線枠内)で0.3以上に着目すると、収入と親のしつけの関係性、計算力と文章読解力と暗記量相互の関係性、計画的学習と繰返し学習と学習時間との関係性が高いことがわかりました。
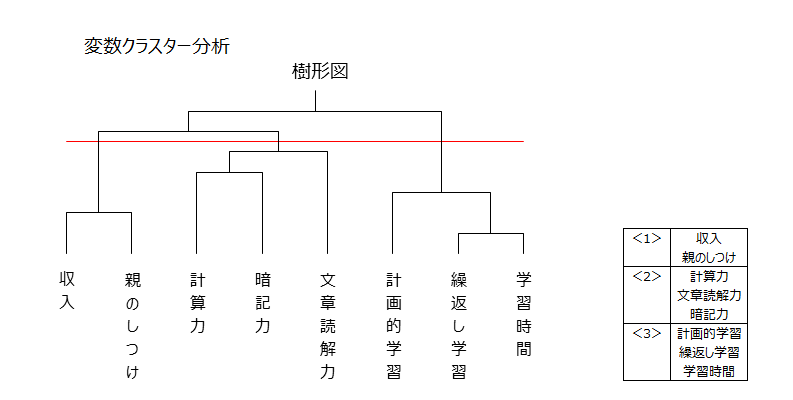
影響要因8項目に変数クラスター分析を行いました。
8項目は3つのグループに分類されることが分かりました。
因果関係の仮説
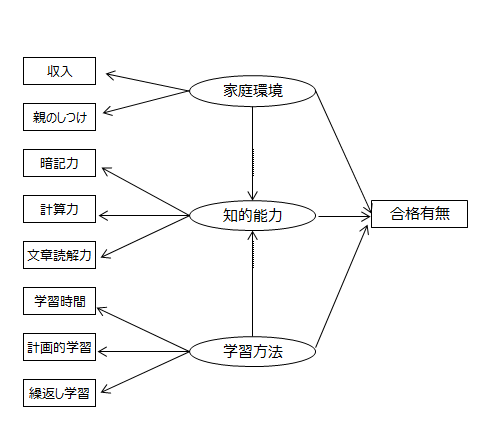
変数クラスター分析の結果から質問項目は3つの群に分類されることがわかりました。これらの群を潜在変数とみなし、因子名を家庭環境、知的能力、学習方法としました。
家庭環境と学習方法は知的能力に影響し、合格有無は家庭環境、知的能力、学習方法の3因子の影響をう受けて決まると考え、下記のパス図を作成しました。
共分散構造分析の実施
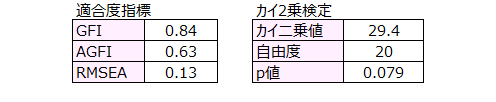
上記パス図で共分散構造分析を行いました。
GFIは0.9を下回りましたが、p値は0.05を上回りました。
パス係数(標準化解)をパス図に表記しました。
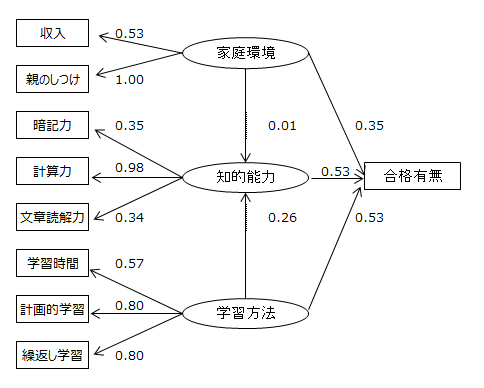
上記パス図に合格総合能力という潜在変数を加えて共分散構造分析をしてみました。
GFIは0.9を超えました。
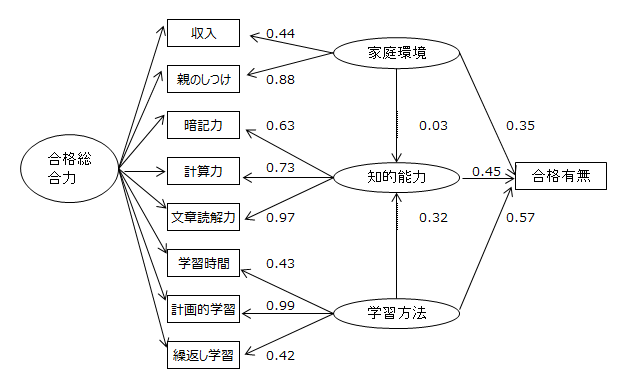
この図を最終のものとして解釈します。
- 【家庭環境】は「収入」と「親のしつけ」ですが、「親のしつけ」が主流です。
- 【知的能力】は「暗記力」「計算力」「文章読解力」の3つですが、いずれも0.5を超え、【知的能力】を構成する重要3要因といえます。なかでも「文章読解力」は重要です。
- 【学習方法】は「学習時間」「計画的学習」「繰返し学習」の3つですが、「繰返し学習」が主流です。
- 【知的能力】は学習方法の影響を受けていますが、【家庭環境】の影響は受けていません。
- 【家庭環境】【知的能力】【学習方法】から合格有無へのパス係数は0.4~0.6の値を示し、合格有無への影響因子といえます。因子の影響順位は【知的能力】【学習方法】の順です。
- 合格の秘訣は、「文章読解力を高めて、学習時間を増やす」となります。
