1.箱ひげ図による外れ値の検出
集団に属するデータにおいて、値の大きい(小さい)データがあるとき、このデータは他と比べて極端に大(小)といえた場合、このデータを「外れ値」とします。
データが正規分布に従っていることが分からない場合は箱ひげ図を、正規性が分かっているときは、次ページで示すスミルノフ・グラブス検定を用いて分析します。
箱ひげ図を用いる場合、上内境界点より大、あるいは下内境界点より小のデータを外れ値とします。
箱ひげ図とは
箱ひげ図は、データを視覚的に要約するためのグラフ。
箱ひげ図は下図に示す7つの統計量をグラフにしたものである。
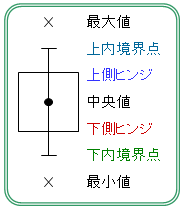
- 上側ヒンジ:第3四分位点
- 下側ヒンジ:第1四分位点
- ヒンジ幅=四分位範囲=第3四分位点-第1四分位点
注. 第1四分位点、第3四分位点は「パーセンタイル・四分位偏差」で解説
下内境界点の計算値=下側ヒンジ-ヒンジ幅×1.5
下内境界点:上記式によって求めた計算値とデータの最小値とを比較し、
計算値<最小値であれば、下内境界点は最小値、
計算値>最小値であれば、下内境界点は計算値
とする。
上内境界点の計算値=上側ヒンジ+ヒンジ幅×1.5
上内境界点:上記式によって求めた計算値とデータの最大値とを比較し、
計算値>最大値であれば、上内境界点は最大値、
計算値<最大値であれば、下内境界点は計算値とする。
例題
次のデータは、ある会社のA支店における30歳未満社員の月給を示したものです。このデータの箱ひげ図を作成よ。

データを並べ替えてから計算する。

四分位範囲=第3四分位-第1四分位=36.25-23.75=12.5 ヒンジ幅=12.5

箱ひげ図
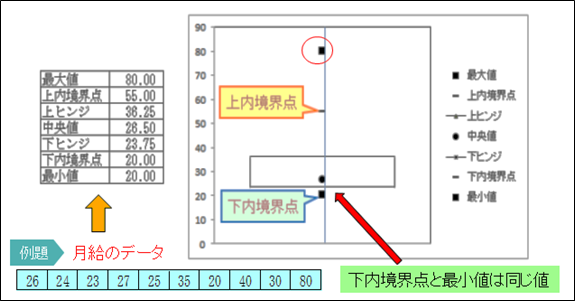
外れ値
上内境界点より大きいデータ、下内境界点より小さいデータが外れ値である。
月給80万円>上内境界点=55万円より、外れ値である。
2.スミルノフ・グラブス検定
データが正規分布に従っていると判断できたとき、スミルノフ・グラブス検定により外れ値を検出できます。
スミルノフ・グラブス検定:Smirnov grubbs’ test

次に求める基準点S0と比べT≧S0なら最大値(あるいは最小値)は外れ値と判断します。

Excelの任意のセルで =tinv(2P/n,n-2)を入力しEnterキーを押す。
この値はExcelの関数で求められます。求め方は例題で示します。

例題
ある会社のA支店における30歳未満社員の月給のデータ(前に記載)について、スミルノフ・グラブス検定を用い外れ値を検出しなさい。
データを大きい順に並べ替えます。


結論 外れ値は15のみ

