母相関係数と比較値の差の検定の概要
母相関係数と比較値の差の検定は、標本相関係数と解析者が定める比較値から、母相関係数が比較値と異なるかを検証する検定方法である。
母相関係数と比較値の差の検定は次の手順によって行う。
母相関係数と比較値の差の検定の手順
①比較する相関係数を定める
②帰無仮説を立てる
母相関係数は比較値である。
③対立仮説を立てる
次の3つの内のいずれかにする。
(1)母相関係数比較値より大きい
(2)母相関係数比較値より小さい
(3)母相関係数と比較値は異なる
③両側検定、片側検定を決める
対立仮説によって自動的に決まる。
対立仮説(1)→ 片側検定(右側検定)
対立仮説(2)→ 片側検定(左側検定)
対立仮説(3)→ 両側検定
④検定統計量を算出
相関係数r 比較値R サンプルサイズn
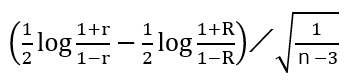
⑤p値の算出
検定統計量はz分布に従う。
両側検定p値は、z分布における検定統計量の上側確率の2倍である。
片側検定p値は、z分布における上側確率である。
⑥有意差判定
p値<有意水準0.05(5%)
帰無仮説を棄却し対立仮説を採択する
母相関係数は比較と異なる(あるいは大きい、小さい)がいえる。
p値≧ 有意水準0.05(5%)
帰無仮説を棄却できず対立仮説を採択しない。
母相関係数は比較と異なる(あるいは大きい、小さい)がいえない。
母相関係数と比較値の差の検定の結果
具体例
今、ある学校で1年生103人をランダムに選び、身長と体重の単相関係数を計算したら0.72だった。
ここ数年の1年生の身長と体重の単相関係数はおよそ0.6である。
検定結果
帰無仮説:今年の1年生の身長と体重の母相関係数は0.6である
対立仮説:今年の1年生の身長と体重の母相関係数は0.6と異なる。
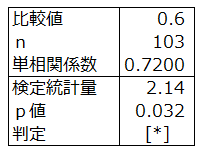
p値0.032<0.05より
今年の1年生の身長と体重の母相関係数は0.6と異なるといえる。



