カイ2乗検定とは何か
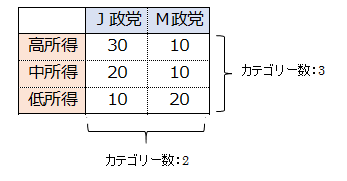
次のクロス集計表は有権者の所得水準と支持政党との関係を調べたものです。
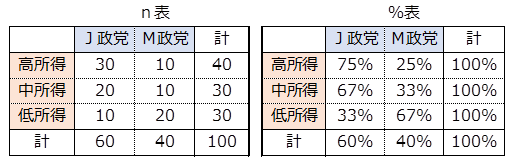
このクロス集計表を解釈すると次のようになります。
Ｊ政党の支持率は高所得層が７５％、中所得層が６７％、低所得層は３３％で、所得が高い層ほどＪ政党の支持率は高くなる傾向がみられます。
Ｍ政党の支持率は高所得層が２５％、中所得層が３３％、低所得層は６７％で、所得が低い層ほどＭ政党の支持率は高くなる傾向がみられます。
このクロス集計表でみられるように、ある特定の所得層である特定の政党支持の比率が高いとき、所得水準と支持政党の項目は関連性があると解釈します。
母集団のＪ政党の支持率が所得階層別に違いがあるかは、母比率の差の検定（対応のない場合）で調べられます。
母集団における所得と政党支持との関連性はこれから学ぶカイ2乗検定で行います。
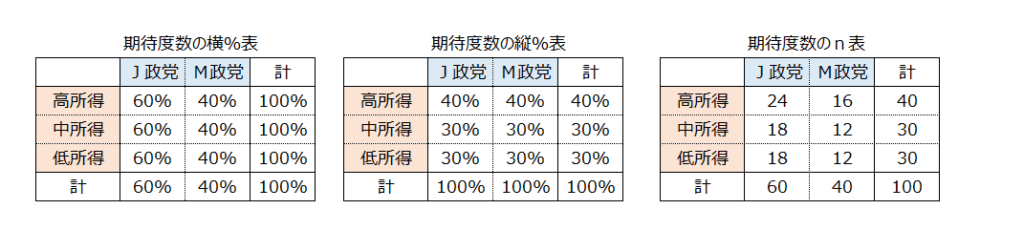
期待度数
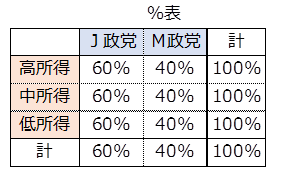
上記のクロス集計表で所得水準と支持政党に関連がないのはどのような場合だと思いますか。
それはどの所得層も計（全体）と同じ比率を示したときです。
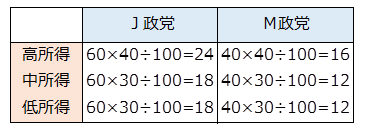
このような比率となる人数は次の計算によって求められることが分かっています。
（回答人数の縦計と横計の数値を掛け、全回答人数で割る）
求められた値を期待度数、元の人数を実測度数といいます。
期待度数＝縦計×横計÷総人数
実測度数
期待度数の横％表では、政党の比率はどの所得層も同じです。
期待度数の縦％表では、所得層の比率はどの政党も同じです。
カイ2乗値
クロス集計表の各セルの回答人数を実測度数といいます。
実測度数が期待度数に近い値であれば関連性が弱く、かけ離れていれば関連性が強いと判断します。
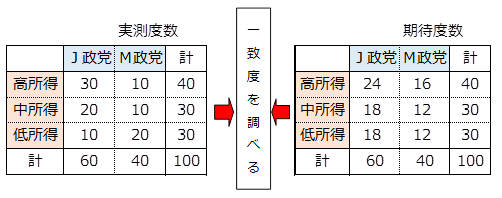
一致度を調べるために、個々のセルごとに次の計算をします
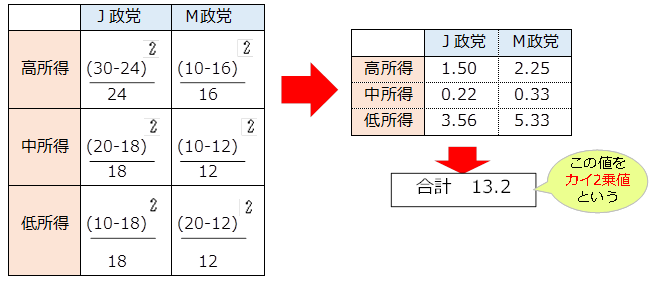
13.2･･･カイ2乗値 → 下記のギリシャ文字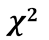 
で表記することがある
カイ2乗値はExcelの関数によって求められます。
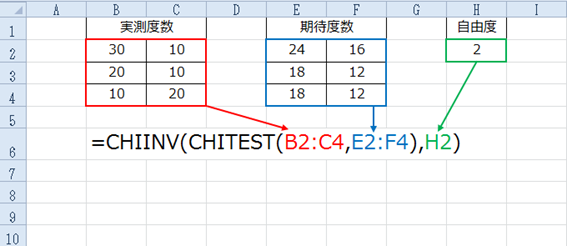
自由度
自由度は表頭項目、表側項目のカテゴリー数によって定められます。
自由度＝（表頭項目カテゴリー数－１）×（表側項目カテゴリー数－１）
＝（２－１）×（３－１）＝２
カイ２乗検定
χ2 値による有意差判定
χ2 値≧Ｃ なら、母集団の所得層と支持政党とは関連性があるといえます。
ただし Ｃ の値はマイクロソフトのExcelで計算できます。
=CHIINV（0.05,自由度）
Ｐ値による有意差判定
Ｐ値＜＝0.05 なら、母集団の所得層と支持政党とは関連があるといえます。
Ｐ値はマイクロソフトのＥｘｃｅｌで計算できます。
任意のセルに次を入力して『Ｅｎｔｅｒｷｰ』 を押します。
=CHIDIST（ χ2 ,自由度）
検定結果
詳しい検定手順は、独立性の検定をご参照ください。
クラメール連関係数の公式
クラメール連関係数 ｒ は独立係数ともいいます。カイ2乗値を用いて求められます。
所得水準と支持政党のクラメール連関係数は
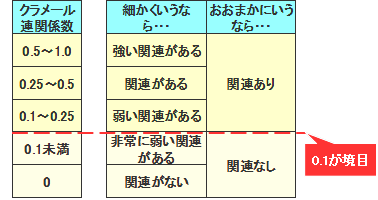
クラメール連関係数の値の検討
クロス集計表の関連性、すなわちカテゴリーデータである2項目間の関連性の強さをを明らかにする解析手法がクラメール連関係数（ｒ）です。
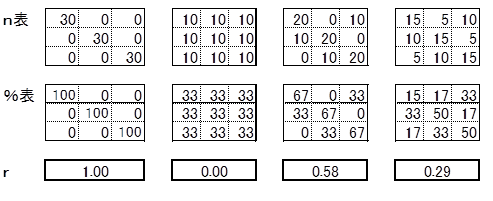
どのようなクロス集計表のとき、ｒ がいくつになるかを下記で確認してみてください。
一番右側の％表でお分かりのように、比率にかなり違いがあっても ｒ はあまり大きくならないことを認識してください。
クラメール連関係数はいくつ以上あればよいか
クラメール連関係数は0～1の間の値です。値が大きいほど関連性は強くなります。
クラメール連関係数はいくつ以上あればよいかを示します。
この相関係数は関連性があっても低めになる傾向があることから、設定を低めにして活用しています。
