標本調査で収集したデータにおける度数は次の集計によって求められる。
| カテゴリーデータ | カテゴリー別(選択肢別)に件数を集計する |
| 数量データ | データをいくつかの範囲に分けたとき、それぞれの範囲内に含まれる件数を集計する |
度数に関する検定は、標本調査より得た単純集計表やクロス集計表の度数(実測度数という)と統計学が定める理論上の期待度数との食い違いの程度から、項目の適合度、正規性、関連性を明らかにすることを目的とする。
度数の検定方法には、適合度検定、独立性検定、1標本コルモゴロフ・スミルノフ検定、2標本コルモゴロフ・スミルノフ検定がある。
適合度の検定 と 1標本コルモゴロフ・スミルノフ検定
度数が単純集計表であるとき、実測度数と期待度数の食い違いから度数分布の適合度や正規性を明らかにする方法である。
2標本コルモゴロフ・スミルノフ検定
2つの単純集計表の分布の違いを明らかにする方法である。
独立性の検定
度数が2項目間のクロス集計表であるとき、実測度数と期待度数の食い違いから2項目間の関連性を明らかにする方法である。
実測度数と期待度数が等しいという帰無仮説のもとで、検定統計量が(近似的に)カイ二乗分布に従うことから、適合度の検定、独立性の検定、コルモゴロフ・スミルノフ検定はカイ二乗検定(χ2検定)とも呼ばれる。
適合度の検定(同等性)と1標本コルモゴロフ・スミルノフ検定の具体例
実測度数と期待度数(正規分布)の違いがないほど、度数分布は正規分布である。
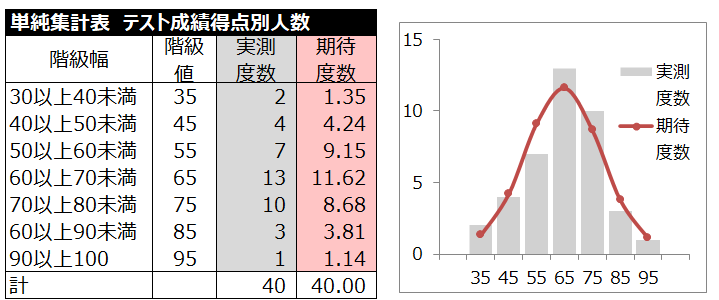
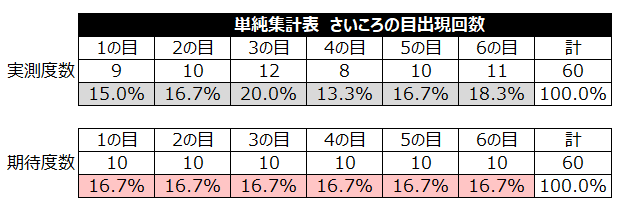
適合度の検定(正規性)と1標本コルモゴロフ・スミルノフ検定の具体例
実測度数と期待度数の違いがないほど、サイコロは正確に作られている。
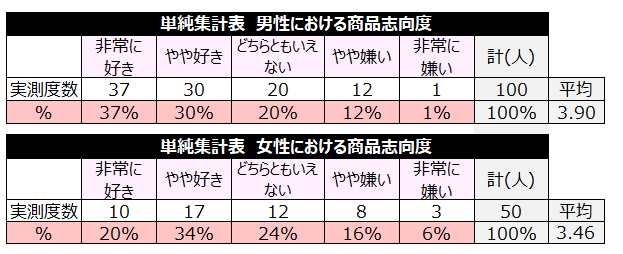
2標本コルモゴロフ・スミルノフ検定の具体例
男性と女性の度数分布(確率分布)の形状に違いがある。
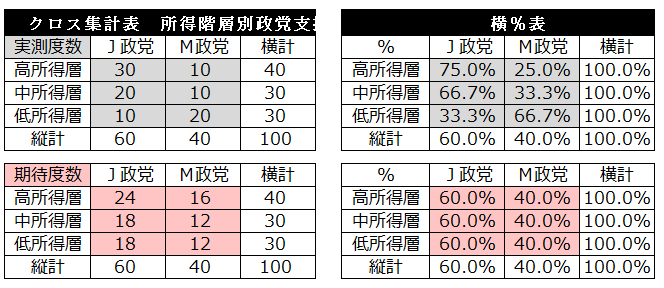
独立性の検定の具体例
実測度数と期待度数の違いがあるほど所得階層と政党の関連性は高くなる。