適合度検定

適合度の検定の概要

適合度の検定はカイ二乗検定の一つで、度数分布（単純集計表）の各度数の同等性や度数分布の正規性を統計的に判定する方法である。

度数分布表の各カテゴリーについて統計学が定める基準に従い期待度数を算出する。同等性を判定する場合の期待度数は全カテゴリーが同じ値、正規性を判定する場合の期待度数は正規分析から算出した理論値である。

観測された実測度数と期待度数の食い違いから検定統計量を算出する。
実測度数と期待度数が等しいという帰無仮説のもとで、検定統計量は（近似的に）カイ二乗分布に従う。
カイ二乗分布を適用し、検定統計量が出現する確率ｐ値を算出し、ｐ値から度数分布の出現度数の同等性や正規性を判断する。
適合度の検定は次の手順によって行う。

適合度の検定の手順

①帰無仮説を立てる

度数分布の実測度数は期待度数に適合する。
度数分布の各カテゴリーの出現度数は同じである。
度数分布は正規分布である。

②対立仮説を立てる

度数分布の実測度数は期待度数に適合しない。
度数分布の各カテゴリーの出現度数は同じでない。
度数分布は正規分布でない。

③両側検定、片側検定を決める

両側検定のみで片側検定はない

④検定統計量を算出

⑤ｐ値を算出

カイ2乗分布を適用

⑥ 有意差判定

ｐ値＜有意水準0.05　対立仮説が言える
ｐ値≧有意水準0.05　対立仮説が言えない

適合度の検定（同等性）の結果

具体例

あるサイコロが不正につくられたものかどうかを調べるために、60回投げて出た目の数を集計した。次の表はその結果である。

このサイコロは不正につくられたサイコロといえるかを有意水準5％で検定せよ。
ただし、正しくつくられたサイコロの１～６の目の出る確率は、全て1/6 で等しいものとする。

1から6の目の出る確率は全て1/6なので、60回投げた時の出現回数は全て10回である。

帰無仮説	サイコロの1～6の目の出る出現回数（実測度数）は期待度数（いずれも10）と同じである。 →サイコロは不正でない。
対立仮説	サイコロの1～6の目の出る出現回数（実測度数）は期待度数（いずれも10）と同じでない。 →サイコロは不正である。

検定結果

ｐ値＞0.05 より対立仮説がいえない。
サイコロは不正であるといえない。

適合度の検定（正規性）の結果

具体例

ある学校で無作為に抽出した40人に記憶力テストをした。
下記はテスト成績の度数分布とヒストグラムである。

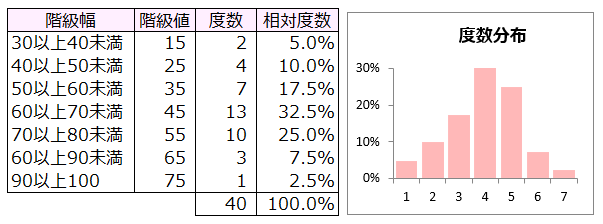
この学校全体における記憶力テストの成績は正規分布であるといえるかを有意水準5％で判断せよ。

検定結果

度数分布に正規分布を当てはめ期待度数（理論度数のこと）を求める。

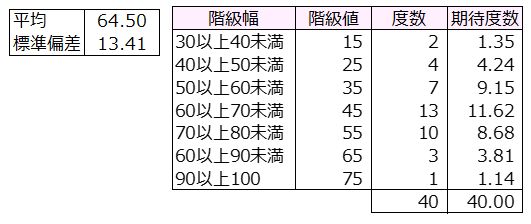
帰無仮説	度数（実測度数）は期待度数と同じである。→正規分布である。
対立仮説	度数（実測度数）は期待度数と同じでない。→正規分布でない。