1. 母平均の差の検定とは
母集団において2つの群の平均値に違いがあるかを調べる方法を母平均の差の検定(The difference between the population mean test)といいます。
製薬会社が解熱剤を開発しました、その新薬Yの解熱効果を明らかにするために10人の患者を対象に、薬剤の投与前と投与後の体温を調べました。体温平均値は、投与前が37.30℃、投与後が36.60でした。
投与前体温平均値から投与後体温平均値を引いた値を低下体温平均値と呼ぶことにします。低下体温平均値は0.70℃でした。


ここでは、母集団における解熱効果を「母平均の差の検定」によってどのように行うかを学びます。母平均の差の検定は色々ありますが。ここでは代表的な3つの検定方法を取り上げます。
①対応のあるt検定 ②t検定 ③ ウエルチt検定
2. 対応のあるデータ、対応のないデータ
調査で収集されるデータには2つのタイプがあります。
- 対応のあるデータ
- 対応のないデータ
下記の左側は同じ対象者についての平均値を比較します。右側は異なる対象者の平均値を比較します。比較するデータが、同じ対象者の場合を対応のあるデータ、異なる対象者の場合を対応のないデータといいます。
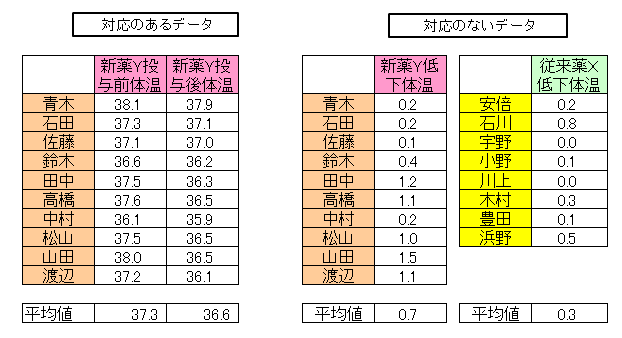
対応のあるデータに用いる検定手法が対応のあるt検定(paired t test)です。
対応のないデータに用いる検定手法が対応のないt検定(unpaired t test)です。
対応のないt検定には、t検定、ウエルチt検定があります。

3. 母平均の差の検定/3つの検定手法の選び方
3つの検定方法はデータタイプだけでなく、サンプルサイズ、母集団の正規性、母集団の等分散性を考慮して選択しなければなりません。
| データタイプ | 対応のあるデータ/対応のないデータ |
| サンプルサイズ | 大きい/小さい |
| 2群各々のデータの母集団での正規性 | 正規分布である/正規分布でない |
| 2群のデータの母集団における分散 (散らばり)の同等性 | 等しい/異なる |
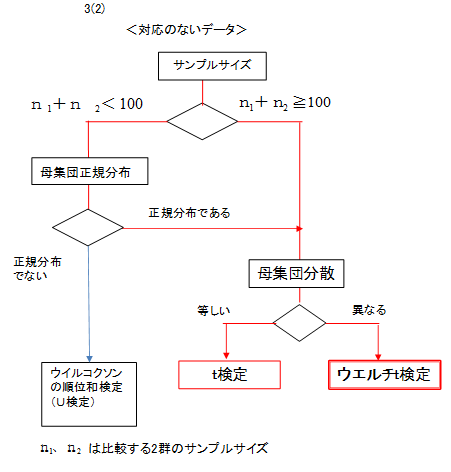
フローチャートで、3つの検定手法の選び方を示します。
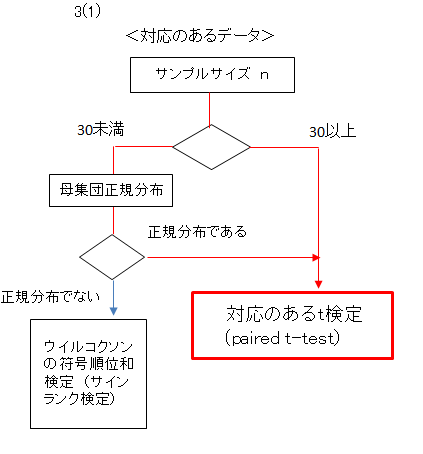
注: ウイルコクソンの符号順位和検定の解説は割愛
ここでは「2(1)」のデータを用い、対応のあるt検定、t検定、ウエルチt検定を解説しています。「2(1)」のデータのサンプルサイズは小さいので、母集団が正規分布であることを調べて、これら3つの検定手法が適用できることを確認しました。

下記の説明は理解しにくいと思いますが、解説を読み終わった時、再読してください。理解できることをお祈りいたします。
- 母集団人数をN=100,000人、比較する2群の平均値をm1、m2 とします。
- m1=m2 とします。
- 母集団は正規分布でないとします。
- この母集団について、サンプルサイズが30人以上(例えばn1+n2=150 人)の調査をして、検定統計量T値を求めます。
- 調査は通常1回ですが多数(1000回)の調査を行い、1000個のT値を求めます。
- T値の分布は正規分布と形状が類似しているt分布となります。
- t検定は、母集団が正規分布でなくとも、T値がt分布になることに基づき行われます。
- n1+n2<30 だとT値の分布はt分布にならず、t検定は適用できません。
4. 母平均の差の検定の仕方
母平均の差の検定の大雑把な仕方を説明します。
調査データに仮説検定の公式を適用し統計量の値を算出します。統計量の値と統計学が決めた基準となる値を比較します。統計量の値が基準となる値より大きいか小さいかで母集団において解熱効果があるかを判断します。
仮説検定によって使われる統計量は次の3つです。
- 信頼区間
- T値
- P値
①信頼区間による仮説検定の仕方を説明します。

②T値による仮説検定の仕方を説明します。
仮説検定の公式によって求めたT値と統計学が決めた基準の値(棄却限界値という)を比較します。
T値>棄却限界値なら新薬Yは解熱効果があると判断します
③P値による仮説検定の仕方を説明します。
仮説検定の公式によって求めたP値と統計学が決めた基準の値(有意点という、通常は0.05)を比較します。
P値<0.05なら新薬Yは解熱効果があると判断します。

5. 母平均の差の検定の手順
母平均の差の検定の基本的な手順を示します。
(1)仮説を2つたてる。
- 「等しい」という仮説をたてる。
統計学では帰無仮説という
帰無仮説は統計学観点からたてる仮説。
【例】母集団の「新薬Yの投与前体温平均値と投与後体温平均値は等しい」 - 「異なる(解熱効果がある)」という仮説をたてる。
統計学では対立仮説という。
対立仮説は分析者が結論(目的)とする仮説。
【例】母集団の「新薬Yの投与前体温平均値と投与後体温平均値は異なる(解熱効果がある)」
(2)調査データについて、平均値、標準偏差、標準誤差を算出する
(3)仮説検定の公式に標準誤差を当てはめ検定統計量を算出する。
検定統計は、信頼区間、T値、P値の3つである。
(4)比較
- 方法1 信頼区間の下限値と上限値の符号が同じか異なるかを比較
- 方法2 T値と棄却限界値を比較
- 方法3 P値と有意点を比較(よく用いられる有意点は0.05 )
(5)判定
3つの方法のいずれかで行う。どの方法を選択しても結論は同じ。
方法1 下限値と上限値の符号が同じ
方法2 T値>棄却限界値
方法3 P値<有意点0.05
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
対立仮説の採択によって、母集団において、異なる(解熱効果がある)がいえる。
このことを、「信頼度95%で有意な差がある」という言い方をする。
【例】
母集団の「新薬Yの投与前体温平均値と投与後体温平均値は信頼度95%で有意な差がある。」
母集団において新薬Yは解熱効果があったといえる。信頼度は95%である。
方法1 下限値と上限値の符号が異なる
方法2 T値<棄却限界値
方法3 P値>有意点0.05
「等しい」という仮説を棄却できず、「異なる」という対立仮説を採択しない。
対立仮説を採択できず、母集団において、異なる(解熱効果がある)がいえない。
このことを、「信頼度95%で有意な差があるといえない」という言い方をする。
【例】
母集団の「新薬Yの投与前体温平均値と投与後体温平均値は信頼度95%で有意な差があるといえない。」
母集団において新薬Yは解熱効果があったといえない。信頼度は95%である。
6. 標準誤差
母平均の差の検定で最初にすることは標準誤差を求めることです。
母平均の差の検定には3つの解析手法がありますが、SE(標準誤差)の式の標準偏差の求め方が異なります。
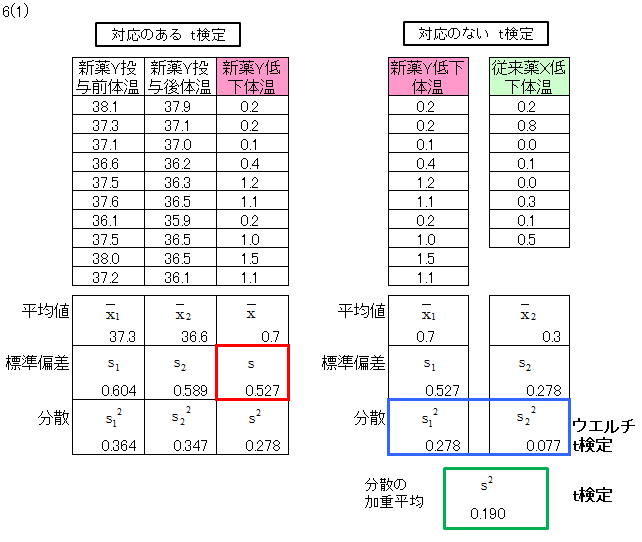
① 対応のあるt検定のSE(標準誤差)
個々の対象者の差分データの標準偏差sを用います。
6(1)の表(左側)における差分データは、新薬Yの投与前体温と投与後の差分で、これを低下体温といいます。
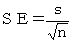
② 対応のないt検定のSE(標準誤差)
対応のないデータなので個々の対象者の差分データは作成できません。したがって、比較する2群の各々のデータの分散(標準偏差の2乗)を用います。
6(1)の表では新薬Y低下体温のs 12 、従来薬X低下体温のs 22 が2群の分散です。
母集団の分散が等しいときの方法なので、2つの群の分散の加重平均を用います。
加重平均 s 2 は次式で算出した値です。
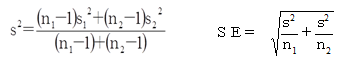
③ ウエルチt検定SE(標準誤差)
t検定同様、比較する2群の各々のデータの分散(標準偏差の2乗)を用います。
6(1)の表では新薬Y低下体温のs 12 、従来薬X低下体温のs 22 。
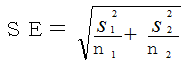
「2(1)」のデータについてSE(標準誤差)を求めます。
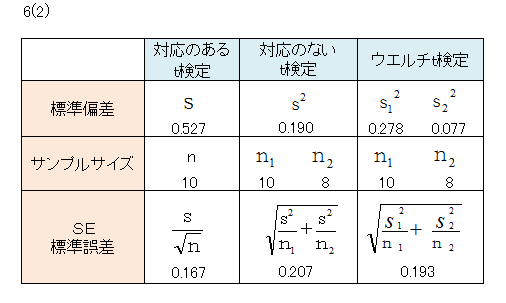
7. 棄却限界値と有意点
前に走り高跳び、リンボーダンスのバーが、T値やP値と比較する棄却限界値、有意点であるという例え話をしました。
棄却限界値と有意点の求め方を習得するには、信頼度、自由度を理解しなければなりません。
信頼度
仮説検定は、母集団での効果(違い)を調べる方法です。効果があるという判断がなされても、その結論は100%正しいといえません。仮説検定は、当る確率が95%となるように作られています。当たる確率を信頼度(statistics confidence)といいます。

自由度
自由度は検定手法の計算式に適用される値で、fで示します。

対応のあるt検定は、投与前から投与後を引いた低下体温を用います。
検定で計算対象の項目(群)は低下体温1つなので、自由度fはその項目のデータ数(n)から1引いた値となります。
対応のないt検定は、新薬Yと従来薬Xで、扱う項目(群)は2つなので、自由度fは2つの項目のデータ数(n1+n2 )から2引いた値となります。

表の下段の数値は「2(2)」のデータについて自由度fを求めたものです。
対応のないt検定とウエルチt検定の自由度を比べると、後者の方が小さな値となります。

棄却限界値とは

棄却限界値の求め方
棄却限界値は有意点と自由度fによって決まります。
棄却限界値の計算は複雑で、手計算ではできません。Excelの関数で求められます。

通常の仮説検定は、信頼度95%で行いますので有意点は0.05です。
信頼度99%で行う場合は、有意点は0.01とします。
「6(1)」の自由度における有意点0.05の棄却限界値を求めると次となります。
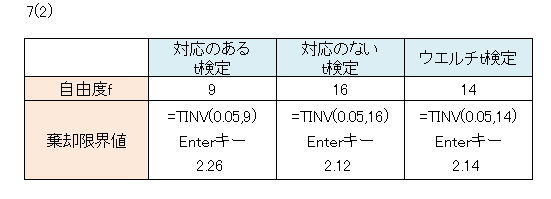
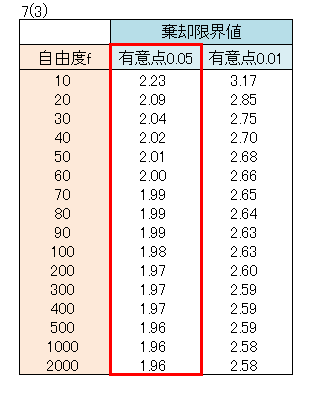
色々な自由度について、棄却限界値を求めてみます。
- 有意点は通常0.05ですが、有意点0.01についても求めました。
- 棄却限界値は、有意点0.05の方が0.01よりちいさくなります。
- 有意点0.05の棄却限界値は、自由度fが500以上は1.96です。
- 有意点0.01の棄却限界値は、自由度fが1000以上は2.58です。
8. 信頼区間
「1(1)」の低下体温の平均値は、新薬Yは2.15℃でしたが別の患者を調べたら異なる値かもしれません。したがって、これから何万人(母集団)の患者に処方されるであろう、新薬Yの低下体温平均値の取りうる範囲を推定しなければなりません。
低下体温平均値の母集団での取りうる範囲を統計学では信頼区間(confidence interval、略名CI)といいます。
母集団平均値の信頼区間は、統計学が定めた値(仮にEとする)と、Eに調査平均値を減算、加算することによって求められます。

Eは、先に学んだ棄却限界値とSE(標準誤差)との掛け算で求められます。

棄却限界値とSEの掛け算で算出するEは、サンプルサイズと標準偏差が小さくなるほど、小さくなります。

ここまでの説明を要約します。
信頼区間の下限値、上限値は次式によって求められます。

SE、棄却限界値の求め方は3つの検定方法によって異なりますので、信頼区間も検定方法によって異なります。
「2(1)」のデータについて、信頼区間を求めてみます。
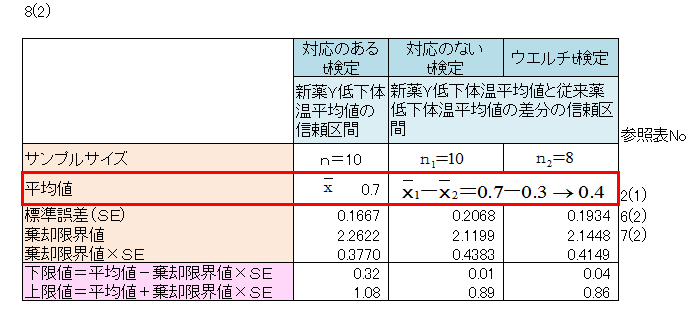

信頼度95%で母集団の平均値の差分を推定できたということです。
対応のないデータに適用するt検定とウエルチt検定の信頼区間を比較してみます。
信頼区間の幅はt検定の方がウエルチt検定より狭くなっています。
母集団の分散が等しい場合はt検定、異なる場合はウエルチt検定を適用します。
母集団の分散が等しい方が信頼区間推定の幅が狭くなるということです。
信頼区間による仮説検定
新薬Yは投与前後で体温平均値に違いがあったか(効果があったか)を、新薬Yの低下体温平均値の信頼区間を用いてどのようして行うかを説明します。

次の低下体温平均値信頼区間のグラフで、AとBの解熱効果を考えみます。
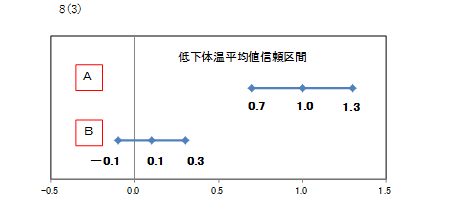
Aの信頼区間は0.7℃~1.3℃です。別の患者について調査したとしても低下体温平均値はこの範囲に収まるということです。もう少しいえば、最も低い0.7℃でもプラスの値だから、解熱効果があるといえます。
Bの信頼区間は-0.1℃~0.3℃です。別の患者について調査したとしても低下体温平均値はこの範囲に収まるということです。Aとの違いは最も低い値が-0.1℃とマイナスになっています。-0.1℃となった場合、低下体温平均値は投与前体温平均値から投与後体温平均値を引いた値なので、投与前体温平均値が投与後体温平均値を下回り、解熱効果がなかったとなります。
信頼区間の下限値、上限値どちらもプラスなら、解熱効果があるといえます。下限値がマイナスで上限値がプラスは、解熱効果があるといえません。

新薬Yの低下体温の仮説検定
- データ 対応がある検定方法
- 対応のあるt検定
- 帰無仮説 新薬Y投与前体温平均値と新薬Y投与後平均値は同じ
- 信頼区間を求める平均値 新薬Y投与前体温平均値と新薬Y投与後体温平均値の差分(新薬Y低下体温平均値)
- 検定に用いる検定統計量 信頼区間の下限値と上限値
- 判定 表8(2)より 下限値=0.26 上限値=1.24
信頼区間は下限値、上限値の符号どちらもプラス。
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは信頼度95%で解熱効果があるといえる。
新薬Y低下体温平均値と従来薬X低下体温平均値の差分の仮説検定
- データ 対応がない
- 検定方法 対応のないt検定
- 帰無仮説 新薬Y体温平均値と従来薬X平均値は同じ
- 信頼区間を求める平均値 新薬Y低下体温平均値と従来薬X低下体温平均値の差分
- 検定に用いる検定統計量 信頼区間の下限値と上限値
- 判定 8(2)より 下限値=0.01 上限値=0.89
信頼区間は下限値、上限値の符号どちらもプラス。
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは従来薬Xに比べ解熱効果があるといえる。
注:ウエルチt検定は割愛しました。
9. T値
仮説検定の3種の神器は信頼区間、T値、P値だと、前に述べました。
信頼区間の説明が終わり、次はT値の説明となります。
T値は平均値をSE(標準誤差)で割った値です。


「2(1)」のデータについてT値を求めます。
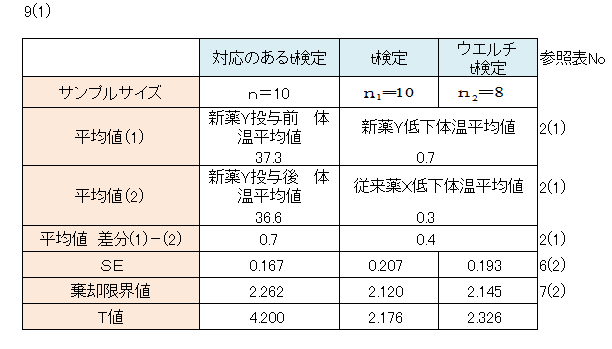
T値による仮説検定
T値を算出する式に代入する平均値は、平均値の差分です。
平均値の差分が大きいということは薬剤の解熱効果あるということです。
したがってT値が大きいほど解熱効果があるということです。
母集団において解熱効果があるかいなかは、統計学が決めた基準の値とT値の比較で行えます。基準の値は先に説明した「棄却限界値」を用います。

新薬Yの低下体温の仮説検定
対応がある
対応のあるt検定
新薬Y投与前体温平均値と新薬Y投与後平均値は同じ
新薬Y投与前体温平均値と新薬Y投与後体温平均値の差分(新薬Y低下体温平均値)
T値と棄却限界値
表9(1)より T値=4.200 棄却限界値=2.262
T値>2.262
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは信頼度95%で解熱効果があるといえる。
新薬Y低下体温平均値と従来薬X低下体温平均値の差分の仮説検定
対応がない
対応のないt検定
新薬Y体温平均値と従来薬X平均値は同じ
新薬Y低下体温平均値と従来薬X低下体温平均値の差分
T値と棄却限界値
「9(1)」より T値=2.176 棄却限界値=2.120
T値>2.120
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは従来薬Xに比べ解熱効果があるといえる。
注:ウエルチt検定は割愛しました。
10. P値
仮説検定の3種の神器は信頼区間、T値、P値だと、前に述べました。
信頼区間、T値の説明が終わり、最後はP値の説明となります。
3つの薬剤A,B、Cの低下体温を調べる調査をしました。
対応のあるt検定を行い、各薬剤の信頼区間、T値を求め、母集団における効果を調べました。
次は信頼区間とT値を図にしたものです。
P値は信頼区間と密接な関係があります。
・P値は、Bのように下限値が0の場合はP=0.05となります。
・AはP値が0.05より小さい値、CはP値が0.05より大きい値になります。
P値はT値とも密接な関係があります。
・T値が大きくなるほどP値は小さくなるという関係があります。
P値とはprobability(確率)の頭文字です。Pの値は0~1の間の値です。
P値は仮説検定でくだした結論の間違う確率を示しています。
P値は小さくなるほど誤る確率は低くなり、母集団において効果がある(違いがある)という結論の確からしさが高まります。
3薬剤のP値は次となります。
AのP値は0なので、効果があるという判断が間違う確率は0%、確からしさは100%です。
BのP値は0.05なので、効果があるという判断が間違う確率は5%、確からしさは95%です。
CのP値は0.43なので、効果があるという判断が間違う確率は43%、確からしさは57%です。
P値(間違う確率)が低ければ効果があると判断はだせますが、P値が高ければ効果があるという判断は出せません。そこで、統計学は5%という基準(有意点という)を設定ました。
P値が有意点5%より小さければ効果がある、大きければ効果なしとします。
P値は手計算で求められませんが、Excelの関数で求められます。
BについてP値を求めます。
対応のあるt検定の自由度はn-1なので、自由度=400-1=399です。
「10(2)」よりT値は1.96です。
=TDIST(1.96,399,2) 「Enter」キー P値0.05が出力される。
P値による仮説検定

新薬Yの低下体温の仮説検定
対応がある
対応のあるt検定
新薬Y投与前体温平均値と新薬Y投与後平均値は同じ
新薬Y投与前体温平均値と新薬Y投与後体温平均値の差分(新薬Y低下体温平均値)
P値と有意点
「9(1)」より T値=4.200 自由度=n-1=10-1=9
Excel関数 =TDIST(4.2,9,2) → P値= 0.00231
P値<0.05
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは信頼度95%で解熱効果があるといえる。
新薬Y低下体温平均値と従来薬X低下体温平均値の差分の仮説検定
対応がない
対応のないt検定
新薬Y体温平均値と従来薬X平均値は同じ
新薬Y体温平均値と従来薬X体温平均値の差分(新薬Yの低下体温平均値)
P値と有意点
「9(1)」より T値=2.176 自由度= n1+n2 -2=10+8-2=16
Excel関数 =TDIST(2.176,16,2) → P値=0.0448
P値<0.05
「等しい」という仮説を棄却し、「異なる」という対立仮説を採択する。
母集団において、新薬Yは従来薬Xに比べ解熱効果があるといえる。
P値と有意点0.5との比較で有意差判定をおこないましたが、P値そのものを使って解釈することもできます。
「母集団において、新薬Yは従来薬Xに比べ解熱効果がある」という判断が間違う確率は3.49%です。
注:ウエルチt検定は割愛しました。
11. 両側検定と片側検定
「5 母平均の差の検定の手順」で、最初にすることは帰無仮説と対立仮説の2つをたてることだと、説明しました。
おさらいします。
「等しい」という仮説をたてる。
【例】母集団の「新薬Yの対か体温平均値と従来薬Xの低下体温平均値は等しい」
「異なる(解熱効果がある)」という仮説をたてる。
【例】母集団の「新薬Yの低下体温平均値と従来薬Xの低下体温平均値は異なる(解熱効果がある)」
対立仮説において、「異なる」でなくて、(高い)あるいは「低い」という仮説をたてることがあります。
上記の例では、母集団の「新薬Yの低下体温平均値は従来薬Xの低下体温平均値より高くなる」といった仮説です。
対立仮説が、「異なる」がいえるかを判断する検定方法を両側検定といいます。
対立仮説が、「高い」あるいは「低い」がいえるかを判断する検定方法を片側検定といいます。
両側検定と両側検定を紹介しましたが、特に理由がないかぎり,片側検定は使いません。
新薬Yは従来薬Xより解熱効果が高いと信じることは悪いことではありませんが、調査をするまでは新薬Yが従来薬Xより解熱効果が高いという情報がないのが通常です。したがって新薬Yは従来薬Xより解熱効果が高いという片側検定は望ましくないと思います。
事前情報がない場合は、「新薬Yと従来薬Xの解熱効果は異なる」の対立仮説を用います。
片側検定におけるP値と棄却限界値の求め方
両側検定、片側検定の解析手順は同じですが、P値と棄却限界値の算出で違いがあります。
P値の求め方
求められたP値の半分(÷2)をP値とします。
棄却限界の求め方
棄却限界値の計算をExcelの関数で行う場合、有意点の2倍とします。

2×有意点における棄却限界値を示します。
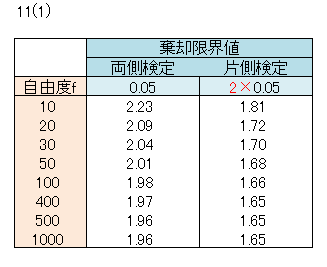
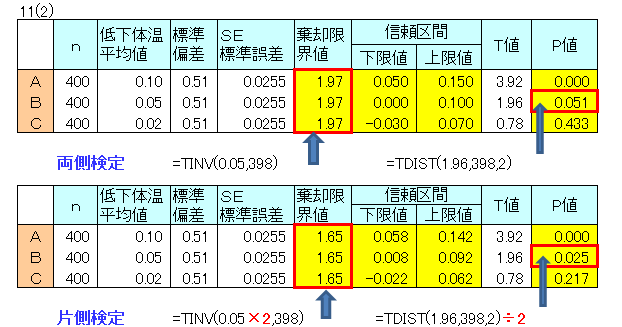
「10(1)」の表について両側検定と片側検定をしました。
このテーマは対応のあるt検定で、投与前と投与後の比較です。
両側検定 Bについて見ると、T値=棄却限界値、P値=0.05で
対立仮説「投与前体温平均値と投与後体温平均値は異なる」は採択できず効果があるといえません。
片側検定 Bについて見ると、T値>棄却限界値、P値<0.05で
対立仮説は「投与前体温平均値は投与後体温平均値より高い」は採択でき、効果があるといえます。
12. 対応のあるt検定_演習
【問題】
ある大手進学塾は、記憶術が記憶力を高めるのに役立つかを調べるために、200人の塾生を対象に、記億術を学習する前と学習した後で記憶力テストを行いました。
テストは100個の単語を5分間で暗記させました。テスト終了の5分後にいくつの単語を覚えているかを調べました。
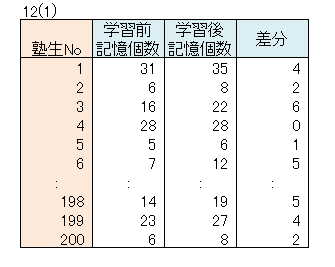
| データタイプ | 同じ塾生の比較なので対応のあるデータ |
| サンプルサイズ | n=200、100以上なので母集団での正規性の確認は不要 |
| 適用する検定手法 | 対応のあるt検定 |
| 帰無仮説 | 記憶術の学習前と学習後で記憶個数平均値は同じ |
| 対立仮説 | 記憶術の学習前と学習後で記憶個数平均値は異なる 記憶術の効果はある 両側検定で行う |
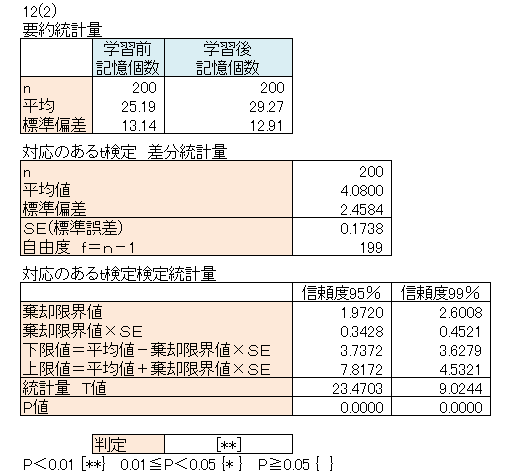
| 計算 | 表外を参照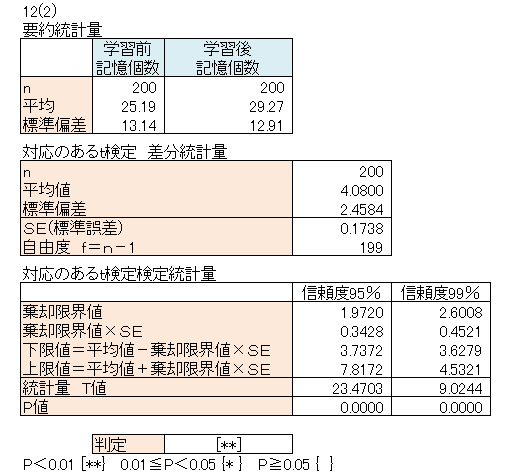 |
| 解釈 | 記憶個数平均値は、学習前が25.2個、学習後が29.3個で、差分平均値は4.1個を示した。 記憶術の学習によって、1人当りの記憶個数は4個増えたことになる。 母集団における記憶個数の差分平均は、信頼度95%で3.7個から7.8個の間にあるといえる。 P値=0.0000<0.05より、帰無仮説を棄却し、対立仮説を採択できる。 母集団において信頼度95%で、記憶術の学習前と学習後で記憶個数平均値は異なる。 すなわち、記憶術の効果はあったといえる。 |
アイスタット社のフリーソフト「Excel統計解析」で演習問題を解きます。
対応のあるt検定を選択します。

実行ボタンを押すと下記が表示されます。
比較するデータの2列を項目名(ラベル)から範囲指定します。
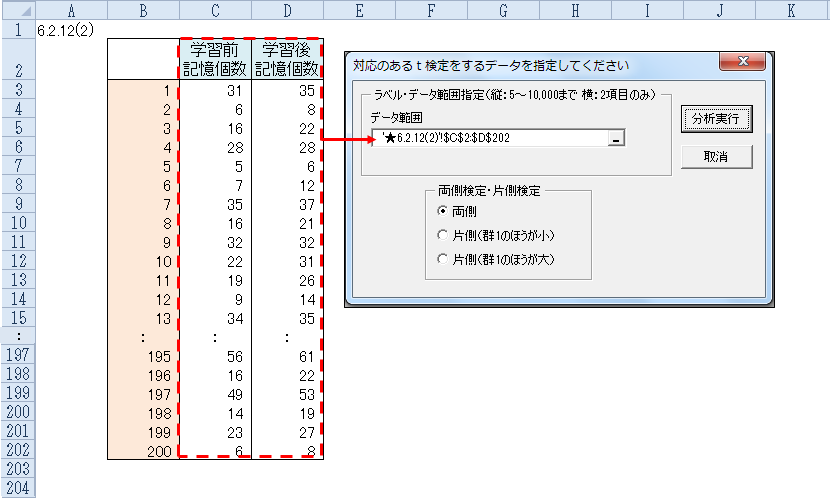
分析実行を押すと、上の結果が出力されます。
13. 対応のないt検定_演習
問題
A市の小学6年生の女子と男子でお年玉金額平均値に違いがあるかを調べるために、女子104人、男子100人を無作為に抽出し、お年玉金額の実態調査をしました。
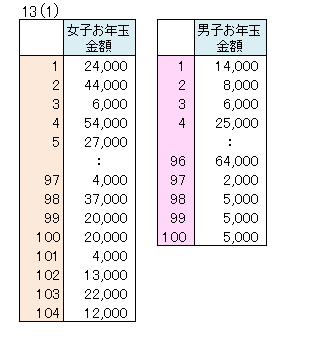
| データタイプ | 女子と男子の比較なので対象者は異なり、対応のないデータ |
| サンプルサイズ | n1+n2=204 、100以上なので母集団での正規性の確認は不要 |
| 母分散の同等性 | 母分散は同じ |
| 適用する検定手法 | t検定 |
| 帰無仮説 | A市の小学生の女子と男子のお年玉金額平均値は同じである |
| 対立仮説 | A市の小学生の女子と男子のお年玉金額平均値は異なる |
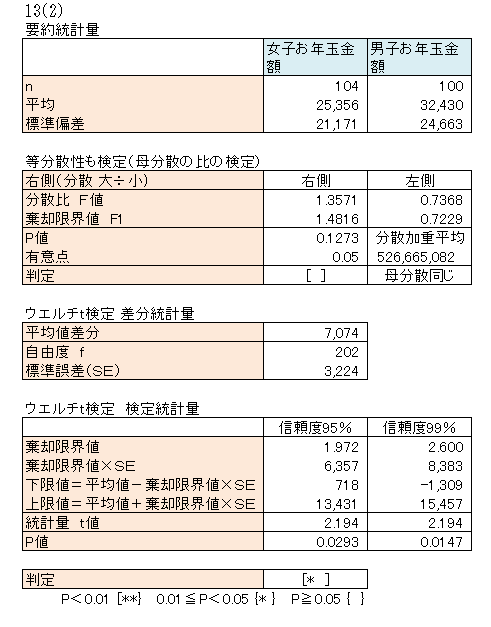
| 計算 | 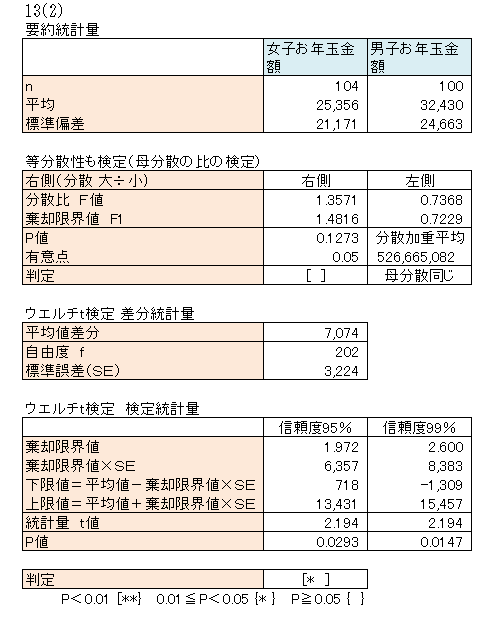 表外を参照 表外を参照 |
| 解釈 | お年玉金額平均値は、女子が25,356円、男子が32,430円で、差分平均値は7,074円を示した。 1人当たりのお年玉金額は男子が女子を7000円ほど上回っていることが分かった。 A市の小学生におけるお年玉金額の差分平均は、信頼度95%で718円から13,431円の間にあるといえる。 P値=0.0293<0.05より、帰無仮説を棄却し、対立仮説を採択できる。 母集団において信頼度95%で、女子と男子ではお年玉金額の平均値は異なるといえる。 |
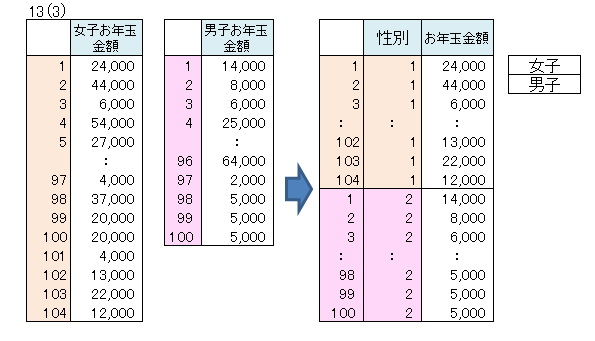
アイスタット社のフリーソフト「Excel統計解析」で演習問題を解きます。
Excelでの入力は右側の形式で入力してください。
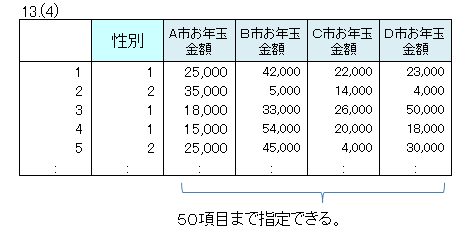
【留意点】
次のように入力すると、1度の処理で母平均の差の検定を50ケースまで行います。
t検定(母平均の差の検定)を選択します。

実行ボタンを押すと下記が表示される。
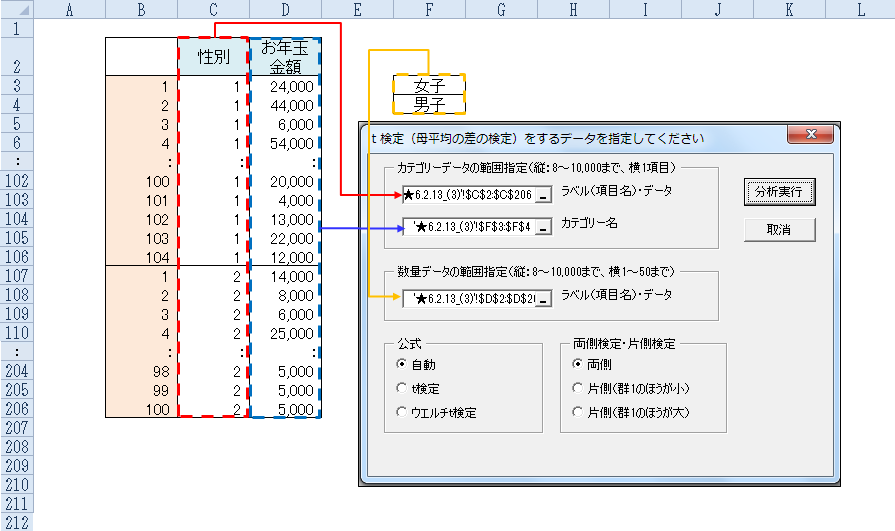
カテゴリデータ(1と2が入力されたデータ)、ここでは性別のデータを、1列、項目名から範囲指定します。
- カテゴリー名、ここでは、女子と男子を範囲指定します。
- 数量データ、ここではお年玉金額を項目名から範囲指定します。
- 公式で、t検定、ウエルチt検定を選択します。
- 「自動」を選択すると、ソフトが母分散の検定をして、その情報に基づき「t検定」「ウエルチt検定」のいずれかを選択します。
- 分析実行を押すと、前の結果が出力されます。

