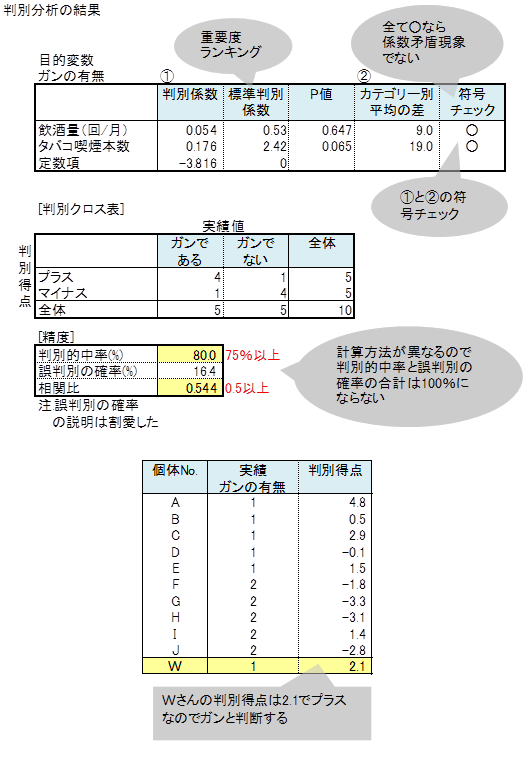
判別分析の応用 ≪ 3/3 ≫
係数矛盾現象が起こる例題
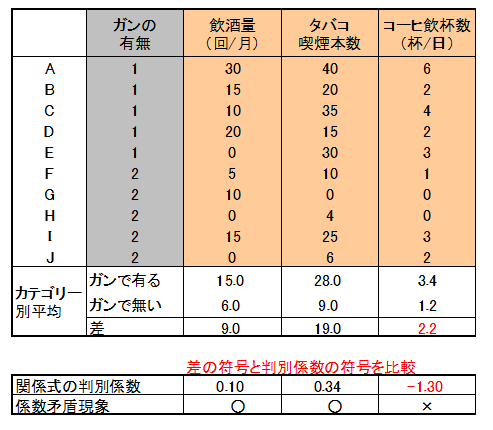
ガンの有無データの説明変数にコーヒー飲杯数を加え、説明変数を3つとしました。このデータに判別分析を処理しました。
判別係数の符号をみると、飲酒量とタバコ喫煙本数はプラス、コーヒー飲杯数はマイナスです。カテゴリー別平均の差の符号をみると、どの説明変数もプラスです。
判別係数の符号とカテゴリー別平均の差の符号が一致していない説明変数があるとき、係数矛盾現象が起こったといいます。
コーヒー飲杯数の判別係数がマイナスになっていますが、係数がマイナスになったこと自体が問題なのではありません。マイナスになったと言うことの意味を吟味する必要があります。
コーヒー飲杯数のカテゴリー別平均の差の符号はプラスです。プラスということは、ガンでない人よりガンである人のコーヒー飲杯数が多いとうことです。それにも関わらず、コーヒー飲杯数の判別係数がマイナスになっていると言うことは、コーヒー飲杯数が多い人ほどガンでないという矛盾した関係を示しています。
説明変数の選択方法
係数矛盾現象が起こらない関係式を得るには、どのような説明変数を用いるかによって決まります。せっかく良いデータがあっても、説明変数の選択方法を知らないために、良くない判別関数式を算出している人がいます。ぜひ次に述べる事柄を理解し、素晴らしい判別関数式を求めてください。
目的変数と相関の高い変数を説明変数にします。相関比を用い、相関比が0.25以上のものを説明変数にするのが一般的です。0.25という値は、必ずしも絶対的なものではなく、1つの目安です。先生の場合、0.1とかなり低い値を設定して、説明変数を多めにとり、次の方法で説明変数の絞り込みを行っています。
<統計学の理論的立場から説明変数を選択>
① 説明変数相互で相関の高い変数を探し、どちらかの変数を落とします。
具体的には相関が0.7以上のときは、どちらかを落とします。この値も1つの目安です。落とし方は、落とす候補になった変数と目的変数との相関をそれぞれ調べて、相関の低い方を落とします。
下記の例では、X1とX2との相関が高いので、どちらかを落とすことになります。 YとX1、YとX2の相関を比べるとYとX2の方が低いので、X2を落とします。

② データが全て同じ値の説明変数は落とします。
<統計学の理論的立場ではなく、分析者の判断から説明変数を選択>
③ 将来設定ができない説明変数を落とします。
④ 施策上不必要とした説明変数を落とします。
係数矛盾現象の対策
上記「説明変数の選択方法①~④」に従うと、係数矛盾現象は起こりません。
例題の説明変数は、下記より「コーヒー飲杯数(杯/日)」を除外し、「飲酒量」「タバコ喫煙本数」のみにすると、係数矛盾現象が起こりません。

判別分析のパソコンソフトによる結果の見方