二元配置分散分析の概要
二元配置分散分析は、群データ(カテゴリーデータ)の項目二つ(XとY)と数量データの項目一つが得られたとき、X項目、Y項目の群別平均の有意差を検証する方法である。
二元配置分散分析で適用できるデータの種別
二元配置分散分析で適用できるデータは3パターンある。
1. セル内のデータ個数は等しくないが、セル内個数は横計個数、縦計個数に比例する
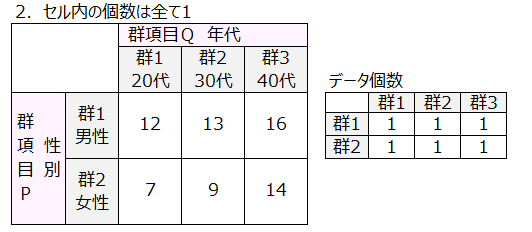
2. セル内のデータ個数は全て1(繰り返しがないデータという)
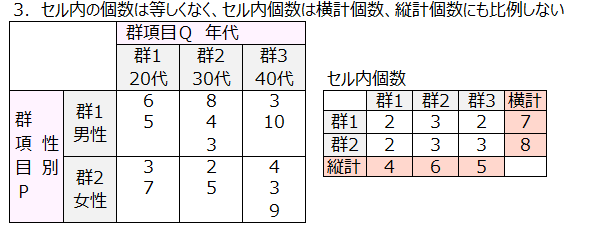
3. セル内のデータ個数は等しくなく、セル内個数は横計個数、縦計個数に比例しない

二元配置分散分析の解析手順
①帰無仮説を立てる
群項目1の各群の母平均は等しい。(群項目1は効果がない)
群項目2の各群の母平均は等しい。(群項目2は効果がない)
群項目1と群項目2は交互作用がない。
②対立仮説を立てる
群項目1の各群の母平均は異なる。(群項目1は効果がある)
群項目2の各群の母平均は異なる。(群項目2は効果がある
群項目1と群項目2は交互作用がある。
③両側検定、片側検定を決める
二元配置分散分析は両側検定のみである。
④分散分析表を算出する
二元配置分散分析における検定統計量は分散比である。
検定統計量(分散比)は、母集団が正規分布、各群の母分散が等しい場合、帰無仮説の基にF布にしたがう。
母集団の正規性、等分散性が崩れても近似的にF分布となる。
したがって分散分析は正規性、等分散性の仮定の違反に関しては比較的頑健な解析手法である。
⑤p値を算出
分散分析表の分散比についてp値を算出する。
p値はF分布における分散比の上側確率である。
p値はExcel関数で求められる。
⑥有意差判定
p値<有意水準0.05
帰無仮説を棄却し対立仮説を採択する
各群の母平均は異なるといえる
交互作用はあるといえる
p値≧有意水準0.05
帰無仮説を棄却できず対立仮説を採択しない
各群の母平均は異なるといえない
交互作用はあるといえない
二元配置分散分析の結果
具体例
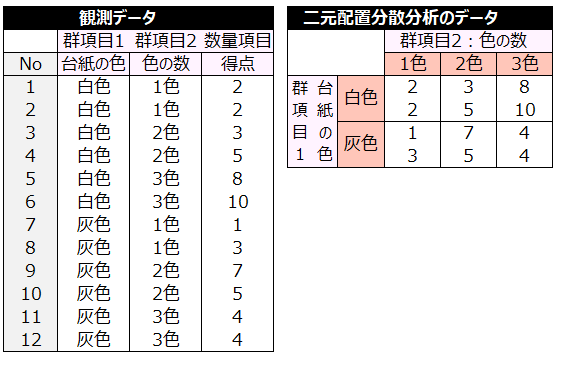
あるポスターの評価テストをした。
群項目は「ポスターの台紙の色」と「ポスターに使用した色の数」の2つ。
・「ポスター台紙の色」は、白色、灰色の2群
・「ポスターに使用した色の数」は、1色(赤)、2色(赤、黄)、3色(赤、黄、黒)の3群
群項目の組み合わせ数は、2×3=6個。
各組合せについて2人ずつ、計12人に10点満点で評価させた。
検定結果
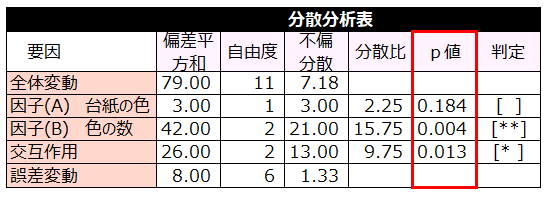
分散分析表より
因子(A)のp値=0.184>有意水準0.05より
台紙の色別の得点の平均は異なるといえない。
台紙の色を変えたことはポスターの評価を上げることに効果があったとはいえない。
因子(B)のp値=0.004<0.05より
色の数別の得点の平均は異なるといえる。
色の数が増えることはポスターの評価を上げることに効果があったといえる。
交互作用のp値=0.013<0.05より
台紙の色と色の数に交互作用があったといえる。
交互作用の解釈
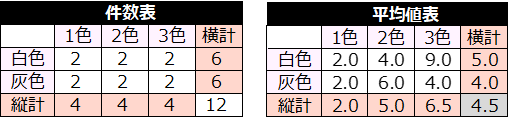
台紙の色別、色の数別の評価得点の平均値をグラフ化すると下図のようになる。
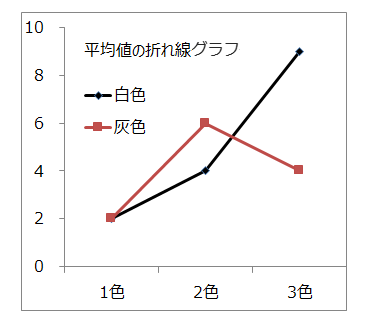
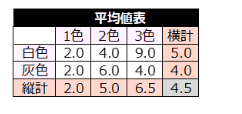
平均値を見ると、台紙の色では、白色が5点で灰色の4点より高くなっている。また、色の数では、1色2点、2色5点、3色6.5点と、色の数が多いほど平均点が高くなる傾向が見られる。
ところが、灰色のポスターだけは、色の数が多くなるほど平均値が高くなるという傾向は見られず、特に灰色で3色使用したポスターでは、平均値が低くなるという結果が出ている。
つまり、灰色で3色という組み合わせに限って、何か平均値を低下させる事柄(効果)があったものと予想される。このような現象を「交互作用がある」という。
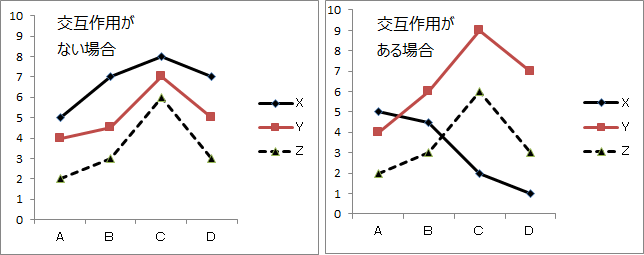
折れ線グラフを見ると、白色と灰色の2本の折れ線は、交差する結果を示している。
一般的に、2つの因子AとBに交互作用があれば折れ線は交差し、交互作用がなければ、それらは平行の形態になる。
対応のある一元配置法は二元配置法(繰り返しがない)を適用
具体例
OL5人に、スーパーで扱っている魚、肉、野菜、果物、惣菜などの名前が書かれた一覧表を渡し、5分間でできるだけ覚えさせた。
時間の経過ごとの記憶個数をテストした。
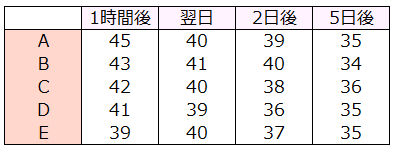
検定結果
対応のあるデータなので、一元配置法でなく二元配置法(繰り返しのない)を適用する。
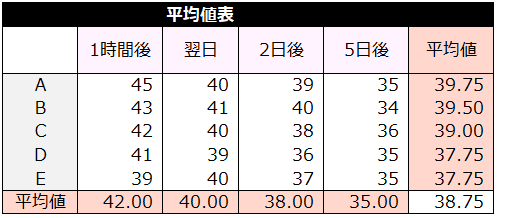
時間の経過にともない、記憶個数の平均は減少している。
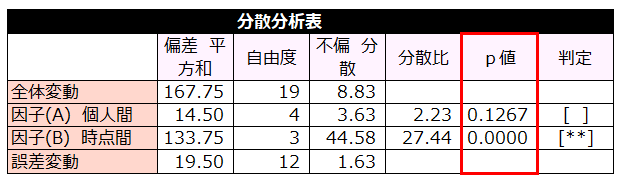
時点間のp値=0.0000<0.05より
時点間の記憶個数の平均に違いがあるといえる。
個人間のp値=0.1267>0.05より
OL5人の記憶力に違いがあるといえない。



