一元配置分散分析の概要
一元配置分散分析は、複数群(3群以上)からなるデータが得られた場合、全ての群の母平均が等しいといえるか否かを明らかにする解析手法である。
一元配置分散分析で把握できること
①3群以上の母平均が異なるかを明らかにする。

②要因の効果を明らかにする。

留意点
①のテーマにおいて、一元配置法から把握できることは3メーカーの性能が異なるかで、H,M,Nのうちどのメーカーがよいとか、個々のメーカー間を比較しMよりHがよいといったことは把握できない。このことを把握したい場合は、一元配置法で3メーカーの評価が異なると判断された後に、多重比較法によるメーカー間相互の有意差検定を行う。
一元配置分散分析の解析手順
①帰無仮説を立てる
各群の母平均は等しい。
②対立仮説を立てる
各群の母平均は異なる。
③両側検定、片側検定を決める
一元配置分散分析は、片側検定のみである。
④分散分析表を算出する

⑤検定統計量を算出
検定統計量は分散分析表の分散比である。
分散比は、母集団が正規分布、各群の母分散が等しい場合、帰無仮説の基にF布にしたがう。
母集団の正規性、等分散性が崩れても近似的にF分布となる。
したがって分散分析は正規性、等分散性の仮定の違反に関しては比較的頑健な解析手法である。
頑健(がんけん)とは
一般的には、ある統計手法が仮定している条件を満たしていない時にも、ほぼ妥当な結果を与えるとき、頑健(robust)である(頑健性を持つ)という
⑥p値を算出
p値はF分布における検定統計量の上側確率である。
⑦ 有意差判定
p値<有意水準0.05
帰無仮説を棄却し対立仮説を採択する。
各群の母平均は異なるといえる。
p値≧有意水準0.05
帰無仮説を棄却できず対立仮説を採択しない。
各群の母平均は異なるといえない。
※ 検定統計量と棄却限界値の比較でも有意差判定は行える。
検定統計量>棄却限界値
帰無仮説を棄却し対立仮説を採択する。
各群の母平均は異なるといえる。
検定統計量≦棄却限界値
帰無仮説を棄却できず対立仮説を採択しない。
各群の母平均は異なるといえない。
一元配置分散分析の結果
具体例
かつて、洗濯機はHメーカー、テレビはMメーカーがよいといわれたことがある。最近は家電製品の性能に差がなくなっているので、価格が安いものを買うのがよいという考え方がある。
このことを検証するために、H,M,Nの3メーカーの洗濯機ユーザーの評価調査を行った。
H使用者4人、M使用者3人、N使用者3人、計10人回答データを示す。なお評価点は10点満点で回答させた。
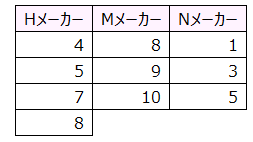
各人の評価から、洗濯機における3メーカーの性能が同じか否かを判断するために、3メーカーの平均を算出した。
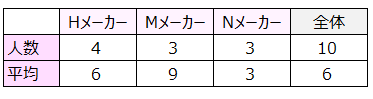
検定結果
分散分析表

p値=0.0103<0.05より
3メーカーの母平均に違いがあるといえる。



