フリードマン検定の概要
フリードマン検定は、ノンパラメトリック検定のひとつで、対応のある3群以上のデータの群間に差があるかを調べる時に用いる。データの大小を順位に置き換えて統計的検定を行うので、3群間の平均値の差というより順位平均値(中央値)の有意差を調べる検定手法といってよいだろう。
データが順序尺度の場合、及び、距離尺度の場合はサンプルサイズが小さいときに用いられる。
距離尺度でサンプルサイズが大きいとき、小さくても全ての群の正規性、分散の同等性が既知の場合は、パラメトリックの一元配置分散分析を適用する。
フリードマン検定は次の手順によって行う。
フリードマン検定の手順
①帰無仮説を立てる
3群以上の母集団の順位平均値は同じである
②対立仮説を立てる
3群以上の母集団の順位平均値は同じでない
③両側検定、片側検定を決める
両側検定のみ片側検定はない
④検定統計量を算出
⑤p値の算出
カイ2乗分布適用
⑥有意差判定
p値<有意水準0.05
3群以上の母集団の順位平均値は同じでないといえる
p値≧ 有意水準0.05
3群以上の母集団の順位平均値は同じでないといえない
フリードマン検定の結果
具体例
対象者10人に、同じジュースの色を3通りに変えて試飲してもらい、おいしさを5点法で評価させた。
(5.おいしい 4.ややおいしい 3.どちらともいえない 2.ややおいしくない 1.おいしくない)
下表はその結果である。
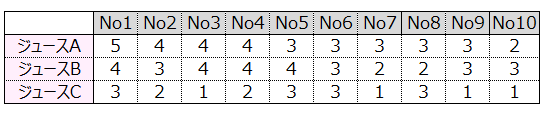
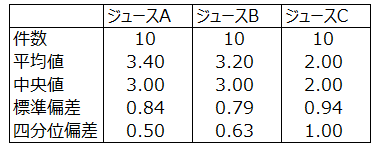
基本統計量
検定結果
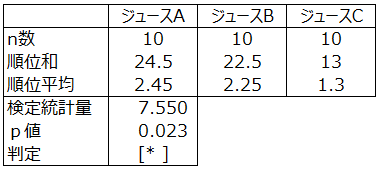
p値0.023<有意水準0.05より、
ジュースのおいしさの評価は、色の影響があったといえる。
判定マーク
[**] 有意水準1%で有意差があるといえる。
[* ] 有意水準5%で有意差があるといえる
[ ] 有意差があるといえない。



