「対応のない場合の母比率の差の検定」の概要
対応のない場合の母比率の差の検定は、対応のないカテゴリーデータに行う手法である。
対応のない場合の母比率の差の検定には3つのタイプがあることを「母比率の差の検定」解説ページで示したが、いずれも検定の手順は同じである。
p値による有意差判定の手順
①帰無仮説を立てる
母集団における群1の割合と群2の割合は同じ。
②対立仮説を立てる
次の3つの内のいずれかにする。
(1)母集団における群1の割合は群2の割合より大きい
(2)母集団における群1の割合は群2の割合より小さい
(3)母集団における群1の割合と群2の割合は異なる
③両側検定、片側検定を決める
対立仮説によって自動的に決まる。
対立仮説(1)→片側検定(右側検定)
対立仮説(2)→片側検定(左側検定)
対立仮説(3)→両側検定
④検定統計量を算出
標本割合をp1、p2とする。検定統計量値=(p_1-p_2)/標準誤差
標準誤差の求め方はタイプ1、タイプ2、タイプ3によって異なる。
⑤p値の算出
検定統計量は帰無仮説が正しいと仮定した場合にz分布に従う。
z分布において、横軸の値(パーセント点)が検定統計量であるときの上側の面積をp値という。
片側検定におけるp値はt分布における検定統計量の上側確率である。
両側検定におけるp値はz分布における検定統計量の上側確率の2倍である。
⑥p値による有意差判定
片側検定(右側検定、左側検定)、両側検定いずれも
p値<有意水準0.05
帰無仮説を棄却し対立仮説を採択 有意差があるといえる。
p値≧有意水準0.05
対立仮説を採択できず、有意差があるといえない。
※有意水準は0.05が一般的であるが、0.01を適用することもある。
割合差分の信頼区間の手順
信頼度95%の信頼区間を次式よって算出する。
(p1-p2)±1.96×標準誤差
下限値=(p1-p2)-1.96×標準誤差
上限値=(p1-p2)+1.96×標準誤差
標本割合をp1、p2とする。
標準誤差の求め方はタイプ1、タイプ2、タイプ3によって異なる。
※ 信頼度99%の信頼区間は定数1.96でなく2.58とする。
信頼区間を適用しての有意差検定を行う
<ケース1>
信頼区間が0をまたがらない。(0より大きい、あるいは、0より小さい)
→比較する2群の母集団割合値は異なる。
<ケース2>
信頼区間が0をまたがる。
→比較する2群の母集団割合値は異なるといえない。
「対応のない場合の母比率の差の検定」の結果
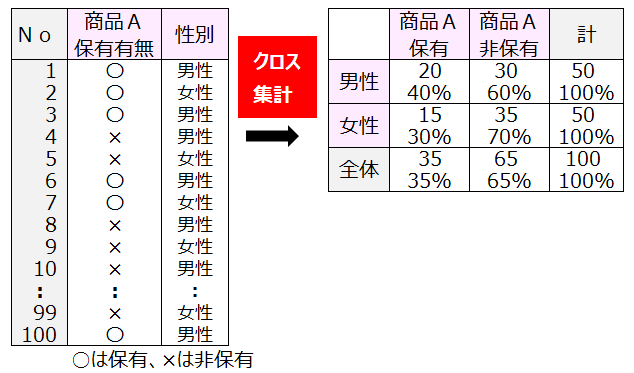
具体例
下記はある町の100人に商品A保有の有無と性別を調査し、クロス集計をした結果である。
検定結果
p値による有意差判定
<1>対応のない場合のz検定を適用
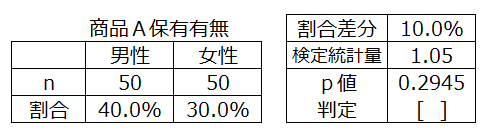
p値>0.05より
この町全体の商品Aの保有割合は、男性と女性で異なるといえない。
<2>従属関係にある場合のz検定を適用
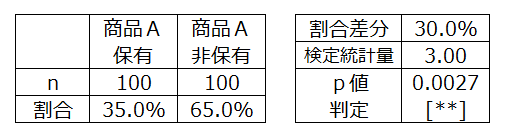
p値<0.05より
この町全体の商品Aの保有割合と非保有割合に違いがあるといえる。
<3>一部従属関係がある場合のz検定を適用
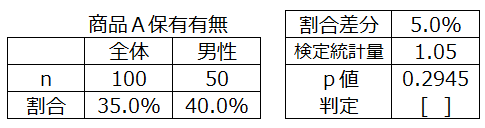
p値>0.05より
この町全体における商品Aの全体保有割合と 男性保有割合に違いがあるといえない。
割合差分の信頼区間
<1>対応のない場合のz検定を適用
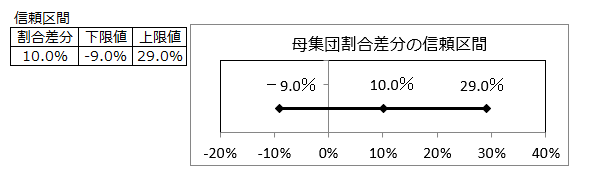
この町全体の男性と女性の商品Aの保有割合差分の信頼区間は、信頼度95%で、-9%~29%の間にあるといえる。
信頼区間は0をまたがるので、商品Aの保有割合は男子と女子は異なるがいえません。
<2>従属関係にある場合のz検定を適用
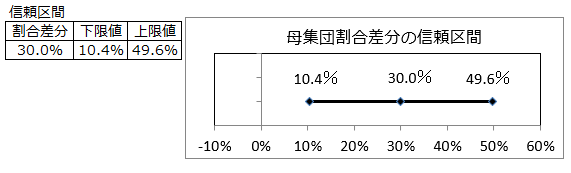
この町全体の商品Aの保有割合と非保有割合の差分の信頼区間は、信頼度95%で、10.4%~9.6%の間にあるといえる。
信頼区間は0をまたがらないので、商品Aの保有割合と非保有割合に違いがあるといえる。
<3> 一部従属関係がある場合のz検定を適用
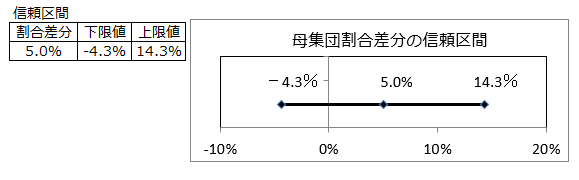
この町全体における商品Aの全体保有割合と男性保有割合の差分の信頼区間は信頼度95%、-4.3%~14.3%の間にある。
信頼区間は0をまたがるので、商品Aの全体保有割合と男性保有割合に違いがあるといえない。



