シェッフェの概要
多重比較シェッフェは、3群以上の群相互の母平均の有意差を調べる対比較の検定と、複数の項目を2グループに分けて2グループの平均値の有意差を調べる対比の検定が行える方法である。
母集団は正規分布、各郡の母分散は等しい、各群のデータ数が異なる場合に適用できる。
メリット
合算した平均値の対比に適用できる
p値が出力される
デメリット
有意差がでにくい
シェッフェの結果
具体例
ある中学校の生徒23人を無作為に選び、4グループA、B、C、Dに分けた。生徒23人について、縄跳びの2重飛び回数をテストした。
ただし、Aの生徒は練習せずに、B生徒は練習したその日に、C生徒は5日間練習した後に、D生徒は2日間練習した後にテストした。
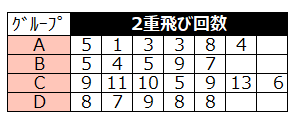
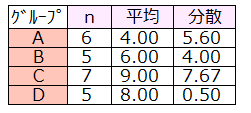
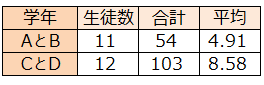
検定結果
(1)
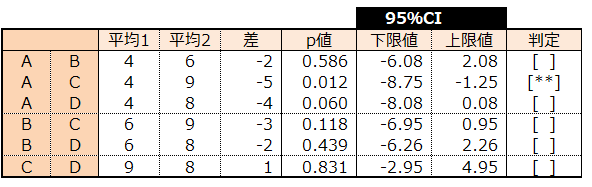
A-Cのp値0.012<0.05より、練習しない生徒群(A)と5日間練習生徒群(C)で有意差が見られた。
他の群間では有意差は見られなかった。
(2)
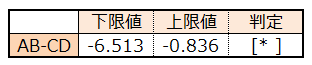
下限値と上限値の範囲が0をまたがっていないので、ABとCDの平均値に差があるといえる。
シェッフェの検定手順
- ①群数をk個とする。
-
k個の組合せの平均値の有意差なのか合算したグループの2グループ間の平均値の有意差なのかを判断する。
- ②比較する組み合わせの検定統計量を算出する。
- ③有意水準0.05、群数、自由度に対するF分布の棄却限界値を算出する。
- ④検定統計量のF分布における上側確率を算出する。
-
p値<0.05なら2群間の母平均は有意差があるといえる。
p値>なら2群間の母平均は有意差があるといえない。 - ⑤比較する平均値の差分の95%CIを算出する。
-
下限値と上限値の範囲が0をまたがなければ2群間の母平均は有意差がある。
下限値と上限値の範囲が0をまたげば2群間の母平均は有意差があるといえない。
※シェッフェ多重比較の対立仮説は比較する群間の母平均は異なるで、両側検定である。(片側検定は対応していない)



