データは数量データとカテゴリーデータに大別されるが、母平均の差の検定は数量データに適用できる手法である。母平均の差の検定は、p値による有意差判定と母平均差分の信頼区間から構成される。
p値による有意差判定とは、2つの母集団から無作為抽出したサンプルの標本平均や標本標準偏差から、2群の母平均が異なるかをp値で調べる方法である。
母平均の差の信頼区間とは、標本平均の差分が母集団の差分であると言い切るのは危険であるので標本平均の差分に幅をもたせて推定する方法である。
母平均の差の検定には多数の検定手法があるが、パラメトリック検定とノンパラメトリック検定の2つに大別される。
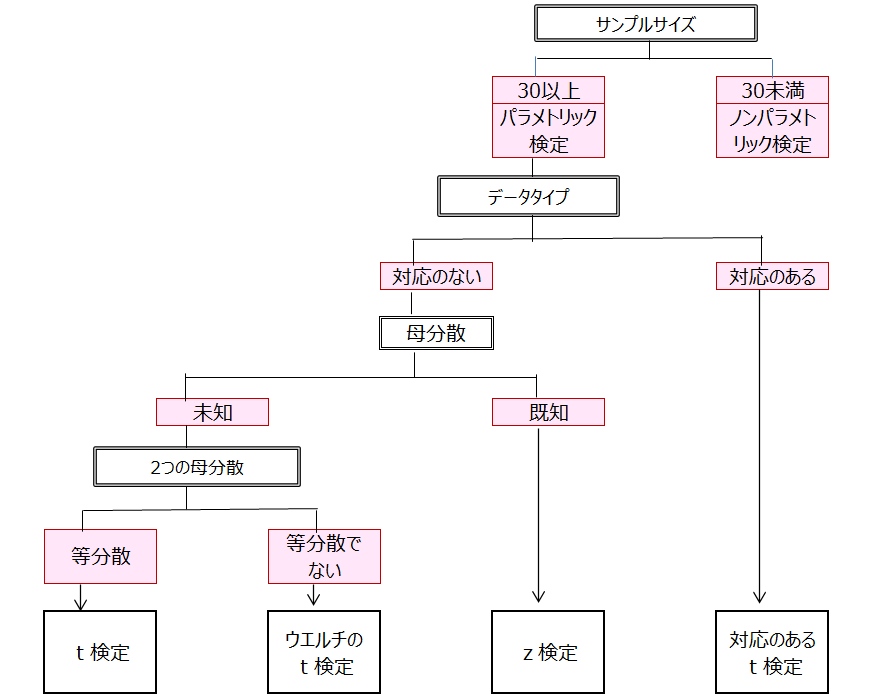
ノンパラメトリック検定は、パラメトリック検定で行うような母集団に対する一切の前提を仮定しない。その代わりに、データにおけるデータの大小の順位、すなわち順序尺度を利用する。
ノンパラメトリック検定は、得られたデータ数が少なく、データが従う分布を仮定することが困難であり、パラメトリック検定を利用することが不適切であると判断される際に利用される。
ノンパラメトリック検定もパラメトリック検定同様に多数の手法がある。
対応のないデータにおける2群の有意差検定はU検定、対応のあるデータはウイルコクソン符号順位和が有名である。
パラメトリック検定とノンパラメトリック検定の使いわけ
ノンパラメトリック検定は、母集団の分布を仮定しない便利な検定法である。基本的には、調査、実験で得られたデータに対する仮説検定の際にはノンパラメトリック検定を実行することは間違いではない。特に、得られたデータサイズが小さいときはパラメトリックな方法で検定すると検出力が低下するため、ノンパラメトリックな方法を選択した方が良い。
しかしながら、欠点も存在する。本来パラメトリック検定を行うことができるデータに対してノンパラメトリック検定を行うと、帰無仮説を棄却できるのにも関わらず帰無仮説を採用してしまう確率が大きく上昇する。得られたデータに対し、適切な検定法を選定することは重要である。



