単相関係数の推定
2変量正規母集団について n 人のサンプルを対象とする標本調査を行い、2変数間の単相関係数 r1 を求めます。
現実的にはありえない話ですが、別のサンプル n 人について標本調査を何回も行い、単相関係数 r2 、 r3 、 r4 ・・・ ri ・・・を得たとします。
求められた相関係数を次式による変換を行い、 r’1 、 r’2 、 r’3 ・・・ r’i ・・・を求め、度数分布及び、ヒストグラムを作成します。(図1)
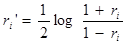
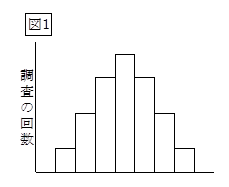
標本調査の回数を多くするほど、図1のヒストグラムは曲線化して行き、正規分布に近づきます。この正規分布は、母集団の単相関係数をρ(ローと読む)とすると
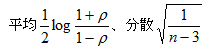
となることが理論的に分かっています。(図2)
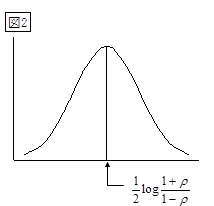
1回の標本調査で行った単相関係数をr とすると
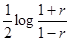
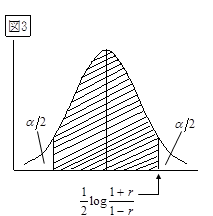
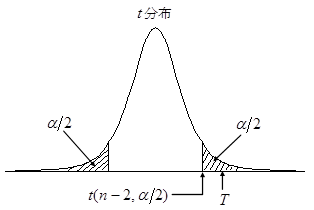
が図3で斜線部分に入る確率は、100(1-α)%です。これより次の公式が導けます。
単相関係数の推定

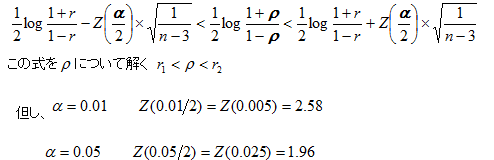
例題
今ある学校で1年生103人をランダムに選び、身長と体重の単相関係数を計算したら0.73でした。
このとき1年生全体の単相関係数を、信頼度95%で推定しなさい。

単相関係数の無相関の検定
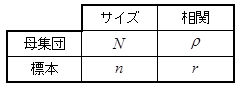
2変量正規分布に従う母集団について、サンプル数が 人の標本調査を何回も行い、それぞれの調査において求めた単相関係数を r1、r2、・・・ ri ・・・とします。
母集団の単相関係数をρとする。母集団の相関がない、すなわちρ=0という仮説をたてると、
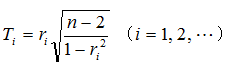
より求められる Ti の度数分布は、自由度 の 分布に従うことが分かっています。
1回の標本調査で得た単相関係数を とすると
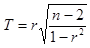
が、有意水準αに対する t(n-2,α/2) より大であれば、この度数分布上でめったにないことが起こったということで仮説を棄却します。すなわち「相関がない」を棄却することがら「相関がある」という結論を出すことになります。
もし、T<t(n-2,α/2)なら「相関がない」を棄却できない、すなわち「相関がない」という結論となります。
単相関係数の無相関の検定

例題
今、ある学校で1年生102人をランダムに選び、入学試験と入学後の学力試験の総合得点の単相関係数を求めたところ0.4でした。
両者の関係は1年生全体において無相関だといえるかを検定しなさい。





