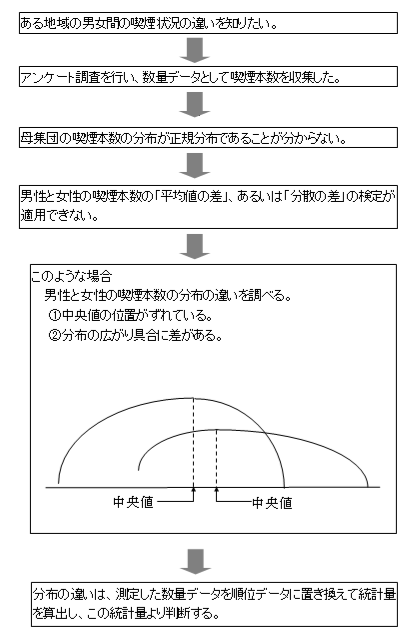
1. ノンパラメトリックの検定とは
統計的検定の大半は、母集団の分布が正規分布に従っていなければ適用できないという制限がありました。母集団の分布がわからない場合は、これから解説するノンパラメトリックの検定を用います。
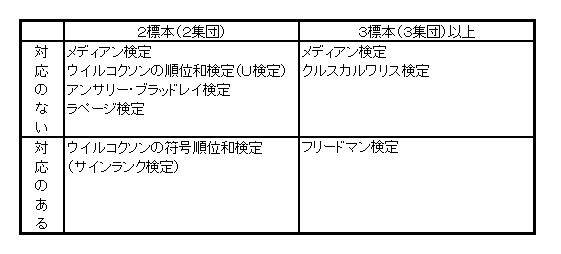
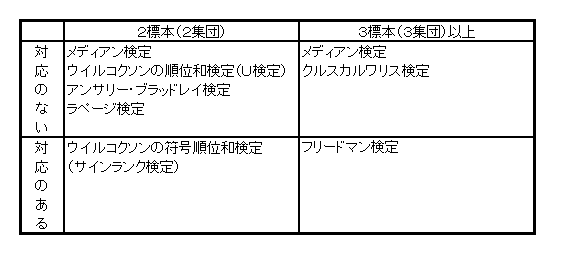
ノンパラメトリックには、数多くの手法がありますが、大半の手法は次の例で示す考え方で検定を行います。
ノンパラメトリックの種類
2. ウイルコクソンの符号順位和検定(サインランク検定)
ウイルコクソンの符号順位和検定(サインランク検定)は、対応している標本に対して2つの母集団の分布に差があるかを検定する手法です。
●公式
データ例(対応している標本)

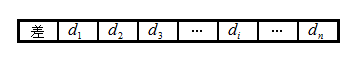
絶対値di の小さい順に順位をつけます。 di が負のもの、正のもの、の順位を加算し、小さい方の値をJ とおきます。
< n が25以上>
次の統計量 は標準正規分布に従います。
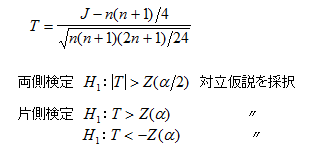

例題
対象者8人に、脂肪分の量の異なる2種類のアイスクリームA、Bを試食してもらい、10点満点でおいしさを評価してもらいました。下表はその結果です。
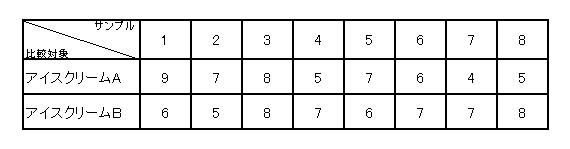
AのアイスクリームはBより評価が高いといえるでしょうか。有意水準0.05で検定しなさい。
解答

3. ウイルコクソンの順位和検定( 検定)
ウイルコクソンの順位和検定は、2つの母集団の分布の中央値に差があるかどうか、つまり2つの分布にずれがあるかどうかを検定する手法です。
標本のデータを順位に置き換え統計量を算出することから順位和検定と名付けられています。この検定方法を 検定という人もいます。
データ例(対応していない標本)
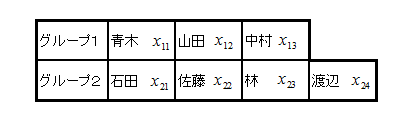
●公式


[例]
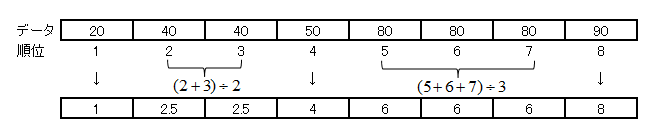

例題
ある高等学校で、2年生と3年生が3000m走の速さに差があるかどうかを調べるために、ランダムに40人選び、3000m走を行いました。次の表はその結果です。
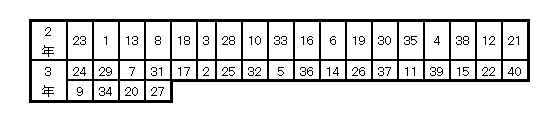
この学校の2年生と3年生は、3000m走の速さに差があるといえるのかどうか、有意水準0.05で検定しなさい。
解答

例題
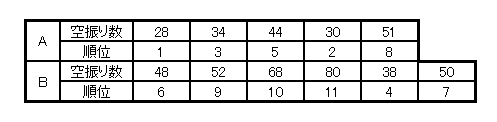
プロ野球2軍登録選手と東京6大学野球レギュラーとでバッティング技術に差があるかを調べるために、各々からランダムに5人、6人を選び、バッティングマシンによるテストを行いました。
下記表は、100回振ったときの空振り数です。これからバッティング技術に差があるといえるでしょうか。有意水準0.05で検定しなさい。

解答


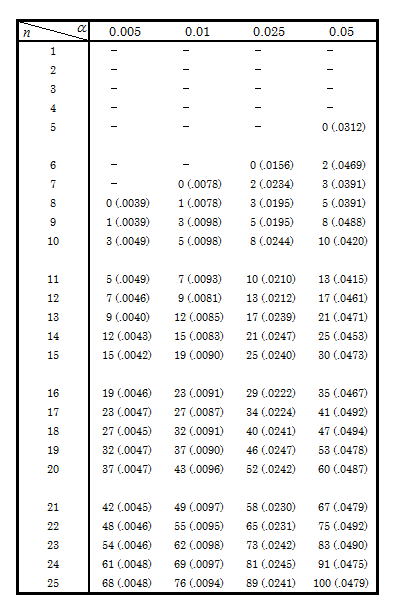
【付表】ウイルコクソンのサインランク表
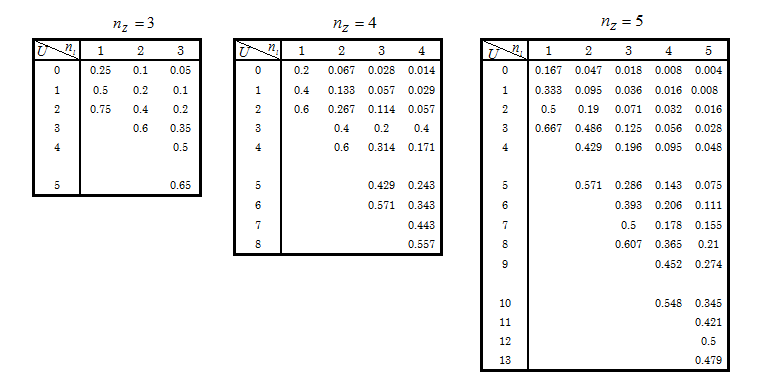
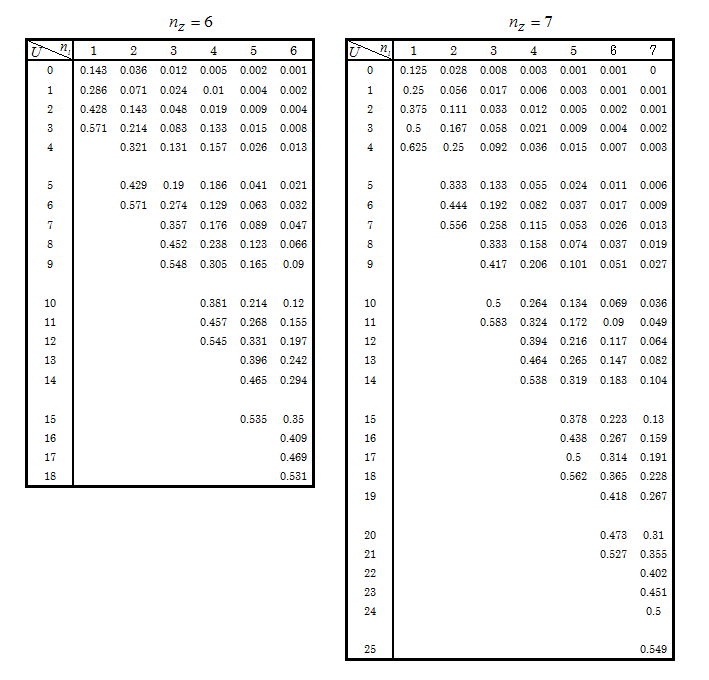
【付表】マン・ホイットニーの U の検定
小標本( NZ =1~8 )のU の 出現確率表
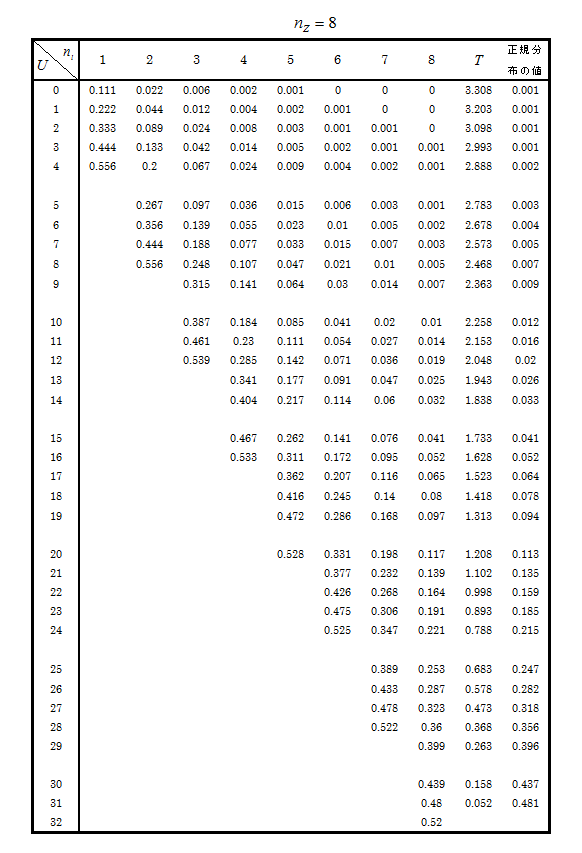
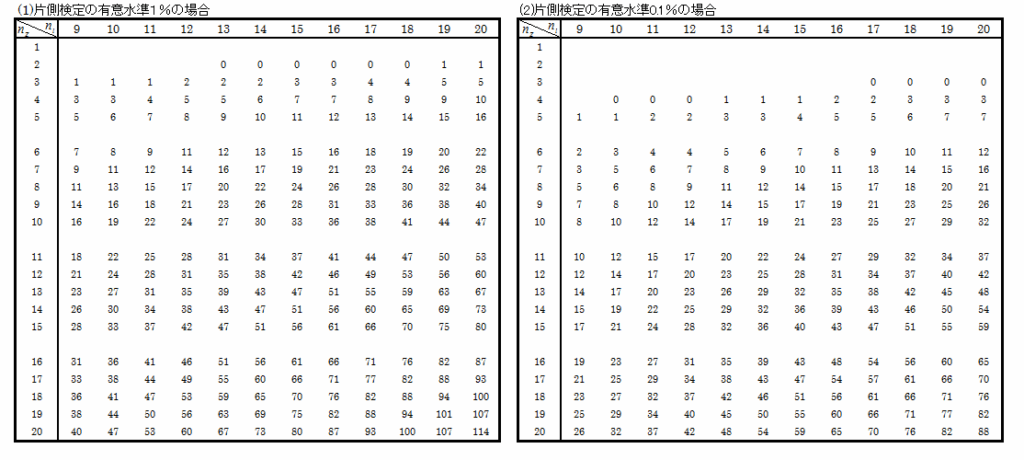
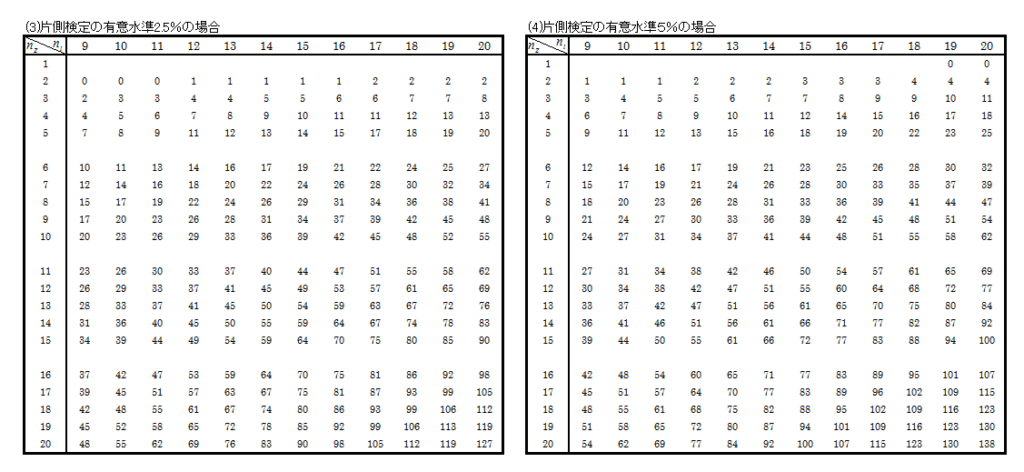
標本数NZ = 9 以上の U の出現確率表